神经网络与深度学习的运用(手写数字识别)
大家好,鉴于上次分享了一篇关于神经网络的文章,这篇文章的目的是为了巩固神经网络知识以及在解决实际问题中对神经网络的优化。关于手写数字识别问题的解决,小编先运用简单的二层前馈神经网络,然后我们再开始对网络进行优化,小编会在二层前馈网络的基础上增加卷积层、池化层以及Dropout层,我们将得到的型网络模型处理手写数字,最后对比前后两者的性能,看看进化后的网络有多。若文章有不妥之处,还望不吝指出。
目录
一、MINST数据集
二、二层前馈神经网络
三、卷积神经网络的诞生
(1)卷积计算
(2)卷积神经网络
(3)池化
(4)Dropout
(5)结合上述,网络完成究极“进化”
四、文章代码合集
一、MINST数据集
我们使用著名的MINIST数据集作为手写数字的数据集。MINIST可以从THE MINIST DATABASE of handwritten digits网站免费下载,通过简单的Keras代码直接读取也很方便。代码如下:
from keras.datasets import mnist
(x_train,y_train),(x_test,y_test) = mnist.load_data()运行后,60000个用于训练的数据被保存到x_train、y_train,10000个用于测试的数据被保存到x_test、y_test。
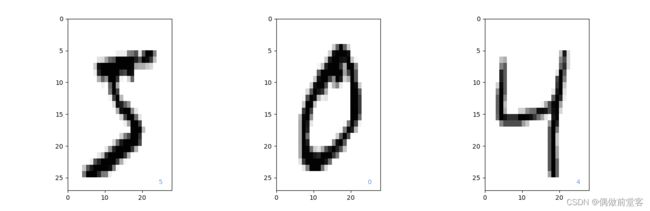
x_train是60000*28*28的数组变量,各元素是0~255的整数值(因为我们的数据都是一张张的图片,所有28*28是它的像素大小,每一个像素的值是0~255之间的整数)。第i个图像可以通过x_train[i,:,:]取出。y_train是长度为60000的一维数组变量,各元素是0~9的整数值,y_train[i]中保存的是与图像i对应的0~9的值。为了对数据有直观的感受,我们用下面的代码来显示x_train前面的3个图像。 (记得导入工具包哦)
plt.figure(figsize=(15,5))
plt.subplots_adjust(wspace=1)#调整子图之间的距离
plt.gray()#将颜色映射设置为灰色
for id in range(3):
plt.subplot(1,3,id+1)
img = x_train[id,:,:]
plt.pcolor(255-img)
#以颜色的深浅把每个位置的值表示出来
#大家试试直接使用plt.pcolor(img)就明白为什么这样表示了
plt.text(24.5,26,"%d" % y_train[id],color='cornflowerblue')
#设置文字说明,前面两个参数设置文字坐标
plt.ylim(27,0)#没有这个y轴的设置,图像会是反过来的
plt.show()图像如下:
二、二层前馈神经网络
我们先来用前面文章介绍的二层前馈神经网络模型对这个手写数字分类问题进行处理,看看效果如何。首先,我们先使用如下代码,将数据转换为容易使用的形式。
from keras.utils import np_utils
x_train = x_train.reshape(60000,784)#将28*28的图像数据当作长度为784的向量处理
x_train = x_train.astype('float32')
#由于网络的输入需要把输入作为实数处理,所有把int类型转换为float类型
x_train = x_train / 255
#归一化,转换为0~1的实数值。为了加快网络的训练速度
num_classes = 10
y_train = np_utils.to_categorical(y_train,num_classes)
#y_train的元素是0~9的整数值,要使用Keras函数np_utils.to_categorical()把它转换为1-of-k表示法的
#编码
#1-of-k表示法: 比如y[1,0,0],那么它就表示0类,y[0,1,0]那它就表示1类,哪一列是1就是哪一类
x_test = x_test.reshape(10000,784)
x_test = x_test.astype('float32')
x_test = x_test / 255
y_test = np_utils.to_categorical(y_test,num_classes),我们输入的是784维的向量。网络的输出层有10个神经元,这是为了确保能对10种数字进行分类。为了使每个神经元的输出值表示的是概率,我们使用Softmax函数作为激活函数。连接输入和输出的中间层我们设置有16个神经元,其激活函数是Sigmoid函数。
np.random.seed(1) #固定随机数,使每次结果基本相同
from keras.optimizers import Adam
from keras.models import Sequential
from keras.layers.core import Dense,Activation
model = Sequential()
model.add(Dense(16,input_dim=784,activation='sigmoid'))
model.add(Dense(10,activation='softmax'))
model.compile(loss='categorical_crossentropy',optimizer=Adam(),metrics=['accuracy'])
#Adam是一种算法,它能使梯度法的性能更好
#注意这里的Adam()在pycharm里面你得将鼠标对着它ALT+SHIFT+ENTER激活
#在别的软件编程我没试过,但是你可以在这之前输入下面这行代码
#adam = keras.optimizers.Adam(learning_rate=0.5,decay=0.0)
#再将Adam()换成adam就可以了
startTime = time.time()
history = model.fit(x_train,y_train,epochs=10,batch_size=1000,verbose=1,validation_data=(x_test,y_test))
score = model.evaluate(x_test,y_test,verbose=0)
print('Test loss:',score[0])
print('Test accuracy',score[1])
print('Computation time:{0:.3f} sec'.format(time.time() - startTime))得到准确率accuray的值为0.86左右,为了确认是否发生过拟合,下面我们将测试数据的误差随epoch变化的情况可视化。
plt.figure(1,figsize=(10,4))
plt.subplots_adjust(wspace=0.5)
plt.subplot(1,2,1)
plt.plot(history.history['loss'],label='training',color='black')
plt.plot(history.history['val_loss'],label='test',color='cornflowerblue')
plt.ylim(0,5)
plt.legend(loc='upper right')
plt.grid()
plt.xlabel('epoch')
plt.ylabel('loss')
plt.subplot(1,2,2)
plt.plot(history.history['accuracy'],label='training',color='black')
plt.plot(history.history['val_accuracy'],label='test',color='cornflowerblue')
plt.ylim(0,1)
plt.legend(loc='lower left')
plt.grid()
plt.xlabel('epoch')
plt.ylabel('acc')
plt.show()得到如下图:
可以看出,训练效果不错,没有发生过拟合。
我们现在训练的效果准确率为0.86,但仍然还是不够理想,那么如何才能使准确率更上一层楼呢?增加中间层的神经元也是一个可行的办法,也可以尝试将激活函数sigmoid换一下,比如换成relu函数等。不过这都不是根本的问题。上诉的这个二层前馈神经网络实际忽视了输入是二维图像,根本没有使用二维空间信息。
对于28*28的输入图像,在输入模型前将其展开为一个长度为784的向量。像素的排列顺序与网络的性能无关。举个例子,即使将所有数据集的图像位置(1,1)的像素值与位置(3,5)的像素值互换,学习到的模型的准确率也完全相同。无论进行多少次这样的互换,即使每个图像已经变得面目全非,网络性能依旧不变。
这是由于网络构造是全连接型的,所有的输入元素都是平等关系,相邻的输入元素与不相邻的输入元素在数学式上完全平等。从这一点可以知道,网络未使用空间信息。而要使用到空间信息,就得用到我们的空间过滤器——卷积核。
三、卷积神经网络的诞生
(1)卷积计算
那么具体来说,空间信息到底是什么呢?空间信息就是直线、弯曲的曲线、圆形及四边形等表示形状的信息。我们可以使用被称为空间过滤器(也可以叫卷积核)的图像处理方法来提炼这样的形状信息。
下图是一个检测纵边的3*3过滤器的例子。移动图像,求出图像的一部分与过滤器元素的乘积之和,直至完成在整个图像上的计算。这样的计算称为卷积计算。
当然过滤器的大小不一定是3*3,也可以是任意大小,但是像5*5、7*7等有中心的奇数大小的过滤器会更便于使用。
下面我们就来对手写数字进行卷积计算。但是在这之前,我们得将数据从原来的一维变成二维的。
x_train = x_train.reshape(60000,28,28,1)#最后一个维度可以看作通道
x_test = x_test.reshape(10000,28,28,1)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
num_classes =10
y_train = np_utils.to_categorical(y_train,num_classes)
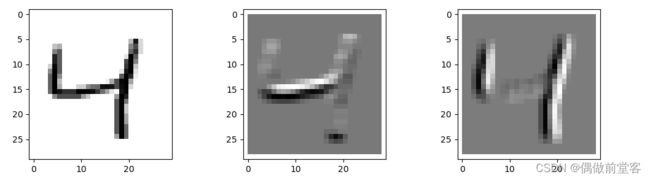
y_test = np_utils.to_categorical(y_test,num_classes)下面通过代码对训练数据中的第3个图像“4”应用检测横边和纵边的两个过滤器。并输出经过过滤器处理后的图像。
x_img = x_train[id_img,:,:,0]
img_h = 28
img_w = 28
x_img = x_img.reshape(img_h,img_w)
out_img1 = np.zeros_like(x_img)
out_img2 = np.zeros_like(x_img)
print(myfil2.reshape(-1))
for ih in range(img_h - 3 + 1):
for iw in range(img_w - 3 + 1):
img_part = x_img[ih:ih+3,iw:iw+3]
out_img1[ih+1,iw+1] = np.dot(img_part.reshape(-1),myfil1.reshape(-1))
out_img2[ih+1,iw+1] = np.dot(img_part.reshape(-1),myfil2.reshape(-1))
plt.figure(1,figsize=(12,3.2))
plt.subplots_adjust(wspace=0.5)
plt.gray()
plt.subplot(1,3,1)
plt.pcolor(1-x_img)
plt.xlim(-1,29)
plt.ylim(29,-1)
plt.subplot(1,3,2)
plt.pcolor(-out_img1)
plt.xlim(-1,29)
plt.ylim(29,-1)
plt.subplot(1,3,3)
plt.pcolor(-out_img2)
plt.xlim(-1,29)
plt.ylim(29,-1)
plt.show()处理后的图像如下(第二个图是经过横边过滤器处理的图像,第三个图是经过纵边过滤器处理的图像)
实际上通过改变过滤器的数值,还可以实现识别斜边、图像平滑化、识别细微部分等各种各样的处理,也就是说通过改变过滤器的值可以得到我们要的空间信息。
然而,应用过滤器之后,输出图像的大小比原来小了一圈,这在有些场景下不太方便。比如在连续应用各种过滤器时,图像会越来越小。针对这个问题,我们通过填充来解决。
填充是在应用过滤器之前,使用0等固定值在图像周围附加元素的方法。在应用3*3的过滤器时,进行宽度为1的填充,图像大小不变。在应用5*5的过滤器时,进行宽度为2的填充即可。
除了填充之外,与过滤器有关的参数还有一个。之前过滤器都是错开1个间隔移动的,但其实错开2个或者3个,乃至任意的间隔都是可以的。这个间隔被称为步长。步长越大,输出图像越小。当通过库使用卷积网络时,填充和步长值会被作为参数传入。
(2)卷积神经网络
好的,现在我们准备将过滤器应用于神经网络了。使用了过滤器的神经网络称为卷积神经网络(Concolution Neural Network,CNN)。
通过向过滤器嵌入不同的数值,可以进行各种图像处理,而CNN可以学习过滤器本身,也就是可以更新过滤器里面的值。我们先创建1个使用了8个过滤器的简单的CNN。对输入图像应用8个大小为3*3、填充为1、步长为1的过滤器。由于一个过滤器的输出为28*28的数组,所以全部输出合在一起是28*28*8的三维数组,我们把它展开为一维的长度为6272的数组,并与10个输出层神经元全连接。代码如下:
model = Sequential()
model.add(Conv2D(8,(3,3),padding='same',input_shape=(28,28,1),activation='relu'))
"""
第一个参数“8,(3,3)”的意思是使用8个3*3过滤器。padding=‘same'的意思是增加1个使
输出大小不变的填充
input_shape=(28,28,1)是输入图像的大小。
由于现在处理的是黑白图像,所以最后的参数为1.如果是彩色图像,则需要指定为3。
这个参数我们也叫通道
activation='relu'的意思是使用relu激活函数
在训练开始之前,过滤器的初始值都是随机设置的。
"""
model.add(Flatten())
"""
卷积层的输出是四维的,
其形式为“(小批量大小,过滤器数量,输出图像的高度,输出图像的宽度)”。
在把这个数据作为输入传给之后的输出层(Dense层)之前,必须先将其转换为二维的形式
“(小批量大小,过滤器数量 * 输出图像的高度 * 输出图像的宽度)”。
这个转换通过model.add(Flatten())进行
"""
model.add(Dense(10,activation='softmax'))
model.compile(loss='categorical_crossentropy',optimizer=Adam(),metrics=['accuracy'])
startTime = time.time()
history = model.fit(x_train,y_train,batch_size=1000,epochs=20,verbose=1,validation_data=(x_test,y_test))
score = model.evaluate(x_test,y_test,verbose=0)
print('Test loss:',score[0])
print('Test accuracy:',score[1])
print("Computation time:{0:.3f}".format(time.time() - startTime))在经过过滤器处理后的神经网络得到的准确值居然达到了可怕的0.97!!!
我们再来看看卷积网络学习到的8个过滤器是怎么样的
plt.figure(1,figsize=(12,2.5))
plt.gray()
plt.subplots_adjust(wspace=0.2,hspace=0.2)
plt.subplot(2,9,10)
id_img = 12
x_img = x_img.reshape(img_h,img_w)
img_h = 28
img_w = 28
x_img = x_img.reshape(img_h,img_w)
plt.pcolor(-x_img)
plt.xlim(0,img_h)
plt.ylim(img_w,0)
plt.xticks([],"")
plt.yticks([],"")
plt.title("Original")
w = model.layers[0].get_weights()[0]
max_w = np.max(w)
min_w = np.min(w)
for i in range(8):
plt.subplot(2,9,i+2)
w1 = w[:,:,0,i]
w1 = w1.reshape(3,3)
plt.pcolor(-w1,vmin=min_w,vmax=max_w)
plt.xlim(0,3)
plt.ylim(3,0)
plt.xticks([],"")
plt.yticks([],"")
plt.title("%d" % i)
plt.subplot(2,9,i+11)
out_img = np.zeros_like(x_img)
for ih in range(img_h - 3 + 1):
for iw in range(img_w - 3 + 1):
img_part = x_img[ih:ih+3,iw:iw+3]
out_img[ih+1,iw+1] = np.dot(img_part.reshape(-1),w1.reshape(-1))
plt.pcolor(-out_img)
plt.xlim(0,img_w)
plt.ylim(img_h,0)
plt.xticks([],"")
plt.yticks([],"")
plt.show()上面的8个图像是过滤器,下面的8个图像是对应过滤器处理后的图像。能够比较明显的看出,第2个过滤器似乎识别了横线下侧的边,第6个过滤器识别了纵边。这种能够自动学习得到过滤器的能力,真是让人为之惊叹。
(3)池化
通过卷积层,我们得以利用二维图像拥有的空间信息,但是在图像识别的情况下,模型要尽量不受图像平移的影响,这一点很重要。假如输入是一个将手写数字“2”平移后的图像,即使只平移1个像素,各个数组中的数值也将完全改变。在人眼里看来几乎完全相同的输入,网络却会识别为完全不同的结果。在使用CNN时也会碰到这个问题。解决这个问题的一种方法就是池化处理。
如下图所展示的就是2*2的最大池化的例子。这种方法着眼于输入图像内的2*2的小区域,并输出区域内最大的数值。然后以步长2来平移小区域,重复同样的操作。最终输出图像的长和宽的大小将变为输入图像的一半。这样即便输入图像发生了平移,输出也会相似,虽然有可能会变,但是平移对我们后面操作的影响变小了。
除了最大池化之外,还有平均池化的方法。在这种方法中,小区域的输出值是区域内数值的平均值。
小区域的大小不一定是2*2,也可以设置为3*3、4*4等任意大小。相应的,步长也可以任意决定,但一般将步长与小区域设置为同样的大小,如小区域大小为3*3,则步长为3。小区域大小为4*4,则步长为4。
(4)Dropout
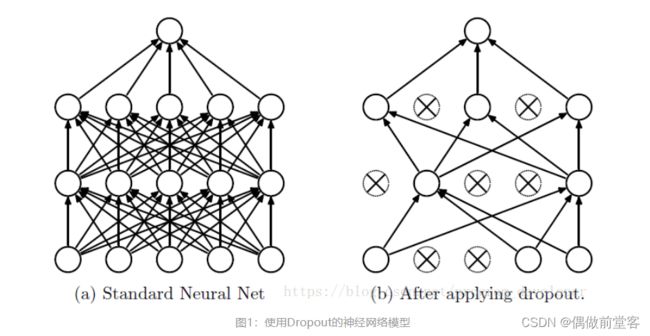
我们在不断优化网络模型的过程中,为了使网络结构更健康,鲁棒性更好,我们会很担心过拟合的问题。而Dropout层就可以很好的解决这个问题。那什么是Dropout呢?
Dropout简单点说:在训练时以概率p(p<1)随机选择输入层和中间层的神经元,并使其他神经元无效。无效的神经元被当作不存在,然后在这样的状态下进行训练。为每个小批量重新选择神经元,重复这个过程。这就相当于在不同的神经网络中进行训练,不同的神经网络得到的结果也是不同的,我们只需要在这些权重结果中取平均值就了。在训练完成后,在进行预测时使用全部的神经元。
Dropout就是通过这样的方式,有效的规避了过拟合问题。
(5)结合上述,网络完成究极“进化”
卷积计算层、池化层它们相当于汽车的“油门”。Dropout层就相当于汽车的“刹车”。神经网络就是我们的“车体”。现在我们就可以开始完成这辆车的组装了。
首先,第1层和第2层是连续的卷积层,提取图像的空间信息。第1层卷积层使用了16个过滤器,那么输出就是16张26*26的图像(没有进行填充,所以图像大小为26*26)。我们把它看作26*26*16的三维数组的数据。
第2层接着对这个三维数据进行卷积。1个3*3的过滤器实质被定义为3*3*16的数组。它的输出为24*24的二维数组(也是因为没有填充)。最后的16的意思是分别分配了16个不同的过滤器,在对它们分别进行处理后,将它们的输出汇总。第2层卷积层有32个这样的大小为3*3*16的过滤器。因此第2层输出为24*24*32的三维数组。如果不算偏置,那么我们需要在第2层定义3*3*16*32个参数。
接着我们第3层的2*2最大池化层,用于处理图像平移带来的影响,图像大小缩小了一半,变为12*12。之后的第4层又是一个卷积层,该层的过滤器有64个,参数数量为3*3*32*64。在第5层我们再次进行最大池化。之后的第6层是神经元数量为128个的全连接层,最后第7层是输出为10个的全连接层。第5层和第6层还引入了Dropout层。代码内容如下:
model = Sequential()
model.add(Conv2D(16,(3,3),input_shape=(28,28,1),activation='relu'))
model.add(Conv2D(32,(3,3),activation='relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
#最大池化层,参数pool_size=(2,2)指定了大小。
model.add(Conv2D(64,(3,3),activation='relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(0.25))
#Dropout层,0.25指的是留下的神经元的比率
model.add(Flatten())
model.add(Dense(128,activation='relu'))
model.add(Dropout(0.25))
model.add(Dense(num_classes,activation='softmax'))
model.compile(loss='categorical_crossentropy',optimizer=Adam(),metrics=['accuracy'])
startTime = time.time()
history = model.fit(x_train,y_train,batch_size=1000,epochs=20,verbose=1,validation_data=(x_test,y_test))
score = model.evaluate(x_test,y_test,verbose=0)
print('Test loss:',score[0])
print('Test accuracy',score[1])
print('Computation time:{0:.3f} sec'.format(time.time() - startTime))
最后得出的准确率达到了惊人的0.993!!!!!!
四、文章代码合集
_train,y_train),(x_test,y_test) = mnist.load_data()
"""
plt.figure(figsize=(15,5))
plt.subplots_adjust(wspace=1)
plt.gray()
for id in range(3):
plt.subplot(1,3,id+1)
img = x_train[id,:,:]
plt.pcolor(255-img)
plt.text(24.5,26,"%d" % y_train[id],color='cornflowerblue')
plt.ylim(27,0)
plt.show()
x_train = x_train.reshape(60000,784)
x_train = x_train.astype('float32')
x_train = x_train / 255
num_classes = 10
y_train = np_utils.to_categorical(y_train,num_classes)
x_test = x_test.reshape(10000,784)
x_test = x_test.astype('float32')
x_test = x_test / 255
y_test = np_utils.to_categorical(y_test,num_classes)
model = Sequential()
model.add(Dense(16,input_dim=784,activation='sigmoid'))
model.add(Dense(10,activation='softmax'))
adam = keras.optimizers.Adam(learning_rate=0.5,decay=0.0)
model.compile(loss='categorical_crossentropy',optimizer=adam,metrics=['accuracy'])
startTime = time.time()
history = model.fit(x_train,y_train,epochs=10,batch_size=1000,verbose=1,validation_data=(x_test,y_test))
score = model.evaluate(x_test,y_test,verbose=0)
print('Test loss:',score[0])
print('Test accuracy',score[1])
print('Computation time:{0:.3f} sec'.format(time.time() - startTime))
plt.figure(1,figsize=(10,4))
plt.subplots_adjust(wspace=0.5)
plt.subplot(1,2,1)
plt.plot(history.history['loss'],label='training',color='black')
plt.plot(history.history['val_loss'],label='test',color='cornflowerblue')
plt.ylim(0,5)
plt.legend(loc='upper right')
plt.grid()
plt.xlabel('epoch')
plt.ylabel('loss')
plt.subplot(1,2,2)
plt.plot(history.history['accuracy'],label='training',color='black')
plt.plot(history.history['val_accuracy'],label='test',color='cornflowerblue')
plt.ylim(0,1)
plt.legend(loc='lower left')
plt.grid()
plt.xlabel('epoch')
plt.ylabel('acc')
plt.show()
"""
x_train = x_train.reshape(60000,28,28,1)
x_test = x_test.reshape(10000,28,28,1)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
num_classes =10
y_train = np_utils.to_categorical(y_train,num_classes)
y_test = np_utils.to_categorical(y_test,num_classes)
id_img = 2
myfil1 = np.array([[1,1,1],[1,1,1],[-2,-2,-2]],dtype=float)
myfil2 = np.array([[-2,1,1],[-2,1,1],[-2,1,1]],dtype=float)
x_img = x_train[id_img,:,:,0]
img_h = 28
img_w = 28
x_img = x_img.reshape(img_h,img_w)
out_img1 = np.zeros_like(x_img)
out_img2 = np.zeros_like(x_img)
print(myfil2.reshape(-1))
for ih in range(img_h - 3 + 1):
for iw in range(img_w - 3 + 1):
img_part = x_img[ih:ih+3,iw:iw+3]
out_img1[ih+1,iw+1] = np.dot(img_part.reshape(-1),myfil1.reshape(-1))
out_img2[ih+1,iw+1] = np.dot(img_part.reshape(-1),myfil2.reshape(-1))
plt.figure(1,figsize=(12,3.2))
plt.subplots_adjust(wspace=0.5)
plt.gray()
plt.subplot(1,3,1)
plt.pcolor(1-x_img)
plt.xlim(-1,29)
plt.ylim(29,-1)
plt.subplot(1,3,2)
plt.pcolor(-out_img1)
plt.xlim(-1,29)
plt.ylim(29,-1)
plt.subplot(1,3,3)
plt.pcolor(-out_img2)
plt.xlim(-1,29)
plt.ylim(29,-1)
plt.show()
model = Sequential()
model.add(Conv2D(8,(3,3),padding='same',input_shape=(28,28,1),activation='relu'))
model.add(Flatten())
model.add(Dense(10,activation='softmax'))
model.compile(loss='categorical_crossentropy',optimizer=Adam(),metrics=['accuracy'])
startTime = time.time()
history = model.fit(x_train,y_train,batch_size=1000,epochs=20,verbose=1,validation_data=(x_test,y_test))
score = model.evaluate(x_test,y_test,verbose=0)
print('Test loss:',score[0])
print('Test accuracy:',score[1])
print("Computation time:{0:.3f}".format(time.time() - startTime))
plt.figure(1,figsize=(12,2.5))
plt.gray()
plt.subplots_adjust(wspace=0.2,hspace=0.2)
plt.subplot(2,9,10)
id_img = 12
x_img = x_img.reshape(img_h,img_w)
img_h = 28
img_w = 28
x_img = x_img.reshape(img_h,img_w)
plt.pcolor(-x_img)
plt.xlim(0,img_h)
plt.ylim(img_w,0)
plt.xticks([],"")
plt.yticks([],"")
plt.title("Original")
w = model.layers[0].get_weights()[0]
max_w = np.max(w)
min_w = np.min(w)
for i in range(8):
plt.subplot(2,9,i+2)
w1 = w[:,:,0,i]
w1 = w1.reshape(3,3)
plt.pcolor(-w1,vmin=min_w,vmax=max_w)
plt.xlim(0,3)
plt.ylim(3,0)
plt.xticks([],"")
plt.yticks([],"")
plt.title("%d" % i)
plt.subplot(2,9,i+11)
out_img = np.zeros_like(x_img)
for ih in range(img_h - 3 + 1):
for iw in range(img_w - 3 + 1):
img_part = x_img[ih:ih+3,iw:iw+3]
out_img[ih+1,iw+1] = np.dot(img_part.reshape(-1),w1.reshape(-1))
plt.pcolor(-out_img)
plt.xlim(0,img_w)
plt.ylim(img_h,0)
plt.xticks([],"")
plt.yticks([],"")
plt.show()
model = Sequential()
model.add(Conv2D(16,(3,3),input_shape=(28,28,1),activation='relu'))
model.add(Conv2D(32,(3,3),activation='relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(64,(3,3),activation='relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128,activation='relu'))
model.add(Dropout(0.25))
model.add(Dense(num_classes,activation='softmax'))
model.compile(loss='categorical_crossentropy',optimizer=Adam(),metrics=['accuracy'])
startTime = time.time()
history = model.fit(x_train,y_train,batch_size=1000,epochs=20,verbose=1,validation_data=(x_test,y_test))
score = model.evaluate(x_test,y_test,verbose=0)
print('Test loss:',score[0])
print('Test accuracy',score[1])
print('Computation time:{0:.3f} sec'.format(time.time() - startTime))