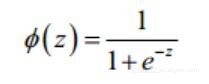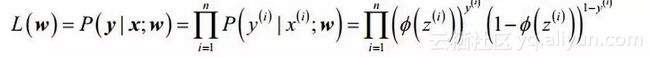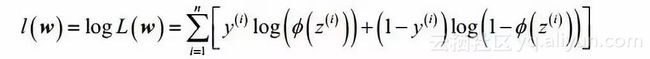【理论+案例实战】Python数据分析之逻辑回归（logistic regression）

简介： 逻辑回归是分类当中极为常用的手段，它属于概率型非线性回归，分为二分类和多分类的回归模型。对于二分类的logistic回归，因变量y只有“是”和“否”两个取值，记为1和0。假设在自变量x1,x2,……,xp，作用下，y取“是”的概率是p，则取“否”的概率是1-p。

逻辑回归是分类当中极为常用的手段，它属于概率型非线性回归，分为二分类和多分类的回归模型。对于二分类的logistic回归，因变量y只有“是”和“否”两个取值，记为1和0。假设在自变量x1,x2,……,xp，作用下，y取“是”的概率是p，则取“否”的概率是1-p。下面将对最为常用的二分类logistic回归模型的原理以及应用进行介绍。（不想看原理的可以直接调至后半部分，有代码演示）

sigmoid函数

在logistic回归的二分类问题中，要用到的函数就是sigmoid函数。sigmoid函数非常简单，他的表达式是

因变量x取值范围是(-∞，+∞)，但是sigmoid函数的值域是(0, 1)。因此不管x取什么值其对应的sigmoid函数值一定会落到(0,1)范围内。它的基本图形如下：

 

（当z为0的时候，函数值为0.5；随着z的增大，函数值逼近于1；随着z的减小，函数值逼近于0.）
生成sigmoid函数图的代码：

import numpy
import math
import matplotlib.pyplot as plt

def sigmoid(x):
    a = []
    for item in x:
        a.append(1.0/(1.0 + math.exp(-item)))
    return a

x = numpy.arange(-10, 10, 0.1)
y = sigmoid(x)
plt.plot(x,y)
plt.yticks([0.0, 0.5, 1.0])
plt.axhline(y=0.5, ls='dotted', color='k')
plt.show()

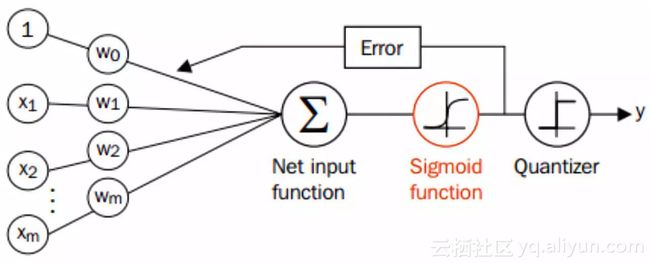
sigmoid函数很适合做我们刚才提到的二分类的分类函数。假设输入数据的特征是(x0, x1, x2, ..., xn)，我们在每个特征上乘以一个回归系数 (w0, w1, w2, ... , wn)，然后累加得到sigmoid函数的输入z：

 

那么，输出就是一个在0~1之间的值，我们把输出大于0.5的数据分到1类，把输出小于0.5的数据分到0类。这就是Logistic回归的分类过程。

基于最优化方法的最佳回归系数的确定

由上，可知logistic回归的大致流程如下，我们要做的就是确定出最佳的w=(w0, w1, w2, ... , wn)。

损失函数与极大似然函数

在logistic回归里面，用极大似然法来求解模型参数。关于似然函数的概念可以参考kevinGao的博客

http://www.cnblogs.com/kevinGaoblog/archive/2012/03/29/2424346.html

先定义似然函数(每个样本都认为是独立的)：

根据似然函数的概念，令似然函数最大的那个概率就是最合理的。我们想最大化似然函数，为方便计算，所以，我们取对数

可知，当权向量 w使l(w)最大的时候,w最合理。

梯度上升法求参数

梯度上升法的基本思想是：要找到某函数的最大值，最好的方法就是沿着该函数的梯度方向搜寻。如果函数为f，梯度记为D，a为步长，那么梯度上升法的迭代公式为：w：w+a*Dwf(w)。该公式停止的条件是迭代次数达到某个指定值或者算法达到某个允许的误差范围。首先对对数的函数的梯度进行计算:

通过矩阵乘法直接表示成梯度:

设步长为α, 则迭代得到的新的权重参数为:

这样我们通过梯度上升法做极大似然估计来做Logistic回归的过程就很清楚了，剩下的我们就需要通过代码来实现Logistic回归吧。

代码实现

数据集：学生的gre，gpa和rank信息作为变量，预测是否admit，若admit=1代表录取，admit=0代表不录取。

import pandas as pd
import statsmodels.api as sm
import pylab as pl
import numpy as np

df = pd.read_csv("binary.csv")

# 浏览数据集
print (df.head())
#   admit  gre   gpa  rank
#0      0  380  3.61     3
#1      1  660  3.67     3
#2      1  800  4.00     1
#3      1  640  3.19     4
#4      0  520  2.93     4

# 重命名'rank'列，因为dataframe中有个方法名也为'rank'
df.columns = ["admit", "gre", "gpa", "prestige"]

#数据统计情况
print (df.describe())
#            admit         gre         gpa   prestige
#count  400.000000  400.000000  400.000000  400.00000
#mean     0.317500  587.700000    3.389900    2.48500
#std      0.466087  115.516536    0.380567    0.94446
#min      0.000000  220.000000    2.260000    1.00000
#25%      0.000000  520.000000    3.130000    2.00000
#50%      0.000000  580.000000    3.395000    2.00000
#75%      1.000000  660.000000    3.670000    3.00000
#max      1.000000  800.000000    4.000000    4.00000

# 频率表，表示prestige与admin的值相应的数量关系
print (pd.crosstab(df['admit'], df['prestige'], rownames=['admit']))
#prestige   1   2   3   4
#admit                   
#0         28  97  93  55
#1         33  54  28  12

拟变量（哑变量）

虚拟变量，也叫哑变量，可用来表示分类变量、非数量因素可能产生的影响。在计量经济学模型，需要经常考虑属性因素的影响。例如，职业、文化程度、季节等属性因素往往很难直接度量它们的大小。只能给出它们的“Yes—D=1”或”No—D=0”，或者它们的程度或等级。为了反映属性因素和提高模型的精度，必须将属性因素“量化”。通过构造0-1型的人工变量来量化属性因素。pandas提供了一系列分类变量的控制。我们可以用get_dummies来将”prestige”一列虚拟化。

# 将prestige设为虚拟变量
dummy_ranks = pd.get_dummies(df['prestige'], prefix='prestige')
print (dummy_ranks.head())
#   prestige_1  prestige_2  prestige_3  prestige_4
#0           0           0           1           0
#1           0           0           1           0
#2           1           0           0           0
#3           0           0           0           1
#4           0           0           0           1

构建需要进行逻辑回归的数据框：

# 除admit、gre、gpa外，加入了上面常见的虚拟变量（注意，引入的虚拟变量列数应为虚拟变量总列数减1，减去的1列作为基准）
cols_to_keep = ['admit', 'gre', 'gpa']
data = df[cols_to_keep].join(dummy_ranks.ix[:, 'prestige_2':])
print (data.head())
#  admit  gre   gpa  prestige_2  prestige_3  prestige_4
#0      0  380  3.61           0           1           0
#1      1  660  3.67           0           1           0
#2      1  800  4.00           0           0           0
#3      1  640  3.19           0           0           1
#4      0  520  2.93           0           0           1

# 需要自行添加逻辑回归所需的intercept变量
data['intercept'] = 1.0

根据上述的数据框执行逻辑回归：

# 指定作为训练变量的列，不含目标列`admit`
train_cols = data[data.columns[1:]]
# sigmoid函数
def sigmoid(inX):  #sigmoid函数
    return 1.0/(1+np.exp(-inX))
#梯度上升求最优参数
def gradAscent(dataMat, labelMat): 
    dataMatrix=np.mat(dataMat) #将读取的数据转换为矩阵
    classLabels=np.mat(labelMat).transpose() #将读取的数据转换为矩阵
    m,n = np.shape(dataMatrix)
    alpha = 0.00001  #设置梯度的阀值，该值越大梯度上升幅度越大
    maxCycles = 300 #设置迭代的次数，一般看实际数据进行设定，有些可能200次就够了
    weights = np.ones((n,1)) #设置初始的参数，并都赋默认值为1。注意这里权重以矩阵形式表示三个参数。
    for k in range(maxCycles):
       h = sigmoid(dataMatrix*weights)
       error = (classLabels - h)     #求导后差值
       weights = weights + alpha * dataMatrix.transpose()* error #迭代更新权重
    return weights

#得到权重
weights=gradAscent(train_cols, data['admit']).getA()
#print (weights)

根据拟合出来的模型，可以进行预测：

# 在这边为方便，我们将训练集拷贝一份作为预测集（不包括 admin 列）
import copy
test_data = copy.deepcopy(data)

# 预测集也要添加intercept变量
test_data['intercept'] = 1.0

# 数据中的列要跟预测时用到的列一致
predict_cols = test_data[test_data.columns[1:]] 

# 进行预测，并将预测评分存入 predict 列中
predict=[]
test=np.mat(predict_cols)
for i in test:
    sum=sigmoid(i*np.mat(weights))
    print (sum)
    if sum <= 0.5:
        predict.append('0')
    else:
        predict.append('1')
test_data['predict']=predict

#计算预测准确率
predict_right=0
for i in range(0,400):
    if int(test_data.loc[i,'admit'])==int(test_data.loc[i,'predict']):
        predict_right=1+predict_right
    else:
        predict_right=predict_right
print ("预测准确率:")
print ("%.5f" %(predict_right/400)) 
#预测准确率:
#0.68250

由上，可知模型预测的准确率为68.25%，但往往我们会改进梯度上升方法以提高预测准确率，比如，改为随机梯度上升法。随机梯度上升法的思想是，每次只使用一个数据样本点来更新回归系数。这样就大大减小计算开销。

def stocGradAscent(dataMatrix,classLabels):
    m,n=shape(dataMatrix)
    alpha=0.01
    weights=ones(n)
    for i in range(m):
        h=sigmoid(sum(dataMatrix[i] * weights))#数值计算
        error = classLabels[i]-h
        weights=weights + alpha * error * dataMatrix[i] #array 和list矩阵乘法不一样
    return weights

同时，还可以改进随机梯度上升法，如下：

def stocGradAscent1(dataMatrix,classLabels,numIter=150):
    m,n=shape(dataMatrix)
    weights=ones(n)
    for j in range(numIter):
        dataIndex=list(range(m))
        for i in range(m):
            alpha=4/(1+i+j)+0.01#保证多次迭代后新数据仍然具有一定影响力
            randIndex=int(random.uniform(0,len(dataIndex)))#减少周期波动
            h=sigmoid(sum(dataMatrix[randIndex] * weights))
            error=classLabels[randIndex]-h
            weights=weights + alpha*dataMatrix[randIndex]*error
            del(dataIndex[randIndex])
    return weights

结语
由上，大家一定对logistic回归有了一定的了解，如果你不愿意自己定义函数调整参数，你也可以调用已有的包来进行logistic回归分类，比如sklearn库中的LogisticRegression，以及statsmodels库中的Logit。

原文发布时间为：2018-07-26
本文作者：胡萝卜酱
本文来自云栖社区合作伙伴“Python爱好者社区”，了解相关信息可以关注“Python爱好者社区”