cuda 编程:矩阵运算讲解
本文主要介绍用CUDA实现矩阵运算(C = A x B)的几个基本方法,帮助大家理解矩阵在GPU上面的运算与CPU上的有何异同,通过实践上手CUDA的优化计算,相比基础方法,能提速10倍以上。
本文内容涉及到CUDA矩阵1D运算,2D运算,共享内存,CUBLAS的使用
文中的全部code:
https://github.com/CalvinXKY/BasicCUDA/tree/master/matrix_multiply
1. CPU矩阵乘运算
矩阵 C = A × B C =A \times B C=A×B的数学运算,是线性代数里面最基本的内容,计算的基本公式如下:
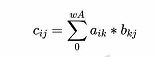
矩阵C中每个元素 c i , j c_{i,j} ci,j为A的第 i i i行与B的 j j j列进行元素对应相乘再求和。
若:A宽wA,高 hA;B宽wB,高hB; C宽 wC,高 hC 。有wA=hB;hC=hA;wC=wB
通过计算机运行我们能够很容易的得到运算部分的代码,如下:
for (unsigned int i=0;i<hA;++i)
{
for (unsigned int j=0; j<wB;++j)
{
float Cij = 0;
for(unsigned int k=0; k<wA;++k)
{
Cij += A[i][k] * B[k][j]
}
C[i][j] = Cij;
}
}
进一步,我们还需要了解矩阵的一维数据运算方式。矩阵的数据在内存中存储的格式是线性格式(行优先/列优先),如下所示,展示的是一种行优先的存储方式。可以通过索引的计算来定位矩阵的某个元素,比如第i行第j列的元素,在线性内存中的位置: i*w+j。w为矩阵的宽度。
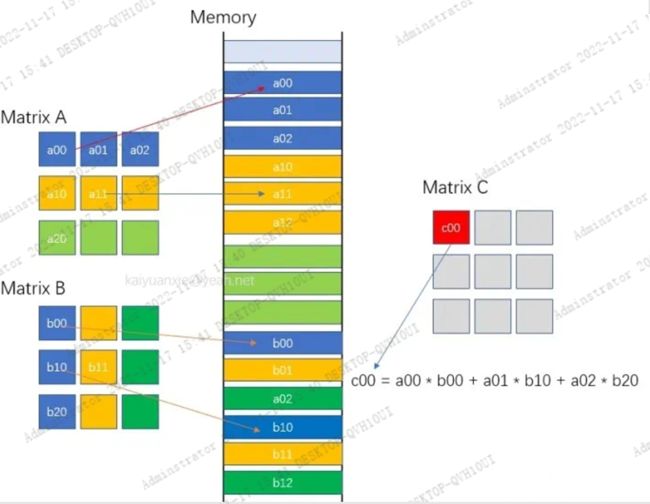
运算的CPU实现代码,如下所示:
/*
* float *C,*A,*B: data pointer of matrix C,A,B each
* unsigned int wA: width of A
* unsigned int wC: width of C,which equals height of B
* unsigned int hC: height of C,which equals height of A
*/
void matrixMulCPU(float *C,const float *A,const float *B,unsigned int wA,
unsigned int wC,unsigned int hC)
{
unsigned int hA=hC;
unsigned int wB=wC;
for(unsigned int i=0;i<hA;++i)
for (unsigned int j=0;j<wB;++j)
{
double sum =0;
for (unsigned int k=0;k<wA;++k)
{
sum += (double)A[i*wA+k] * (double) B[k*wB + j];
}
C[i * WB +j] = (float)sum;
}
}
上述代码采用三重循环实现全部运算。最内层是计算每个Cij元素的运算,再用两个for遍历获得了整个C矩阵的结果。显然,如果用单线程的CPU运算,该过程的计算时间为:
T = h A × w B × w A × d e l t a T T=hA \times wB \times wA \times deltaT T=hA×wB×wA×deltaT
其中hA,wB是矩阵A的高和宽,wB是矩阵B的宽度,deltaT表示每次运算消耗的时间。
由于过程只有一个CPU线程在串行计算,所以矩阵越大耗时越久。为了优化这个过程,我们采用GPU来计算,GPU有大量的线程,通过增加更多的线程来并行计算,降低运算时间。理论上当我们用N个线程来运算时,整个运算时间为
T = h A × w B × w A × d e l t a T / N T=hA \times wB \times wA \times deltaT /N T=hA×wB×wA×deltaT/N
2. 一维块(1D block) 构建运算
多线程的编发计算道理很简单,让多线程分担一个线程的工作量。在NVIDIA的GPU中使用多线程不像CPU中并行一样直接,如C++添加"pragma omprarallel"。GPU中运算涉及数据的转移(CPU <-> GPU)、GPU工作流的创建等内容,但最核心的点是线程thread的运算过程。基本上,我们只需要明确两个问题:
-
- CUDA代码里面的Thread是如何调用的?
-
- 如何让不同的Thread与需要计算的数据匹配?
2.1 CUDA代码里面的Thread是如何调用的?
CUDA 对Thread的调用其实是由编译器完成的。用户在编写代码时主要关注如何定义GPU能运行的函数,其次是如何调用这个函数。定义GPU线程(Thread)可运行函数,实际上就是在函数前面加上一个__global__前缀。
__global__ void functionExample()
{
//code part
}
函数的执行需要用一个特殊的语法<<< ... >>>在主机host上面执行上述函数,尖括号里面实际上是定义执行这个函数用多少线程threads
functionExample <<<numBlocks,threadPerBlock>>>
这里需要知道如果调用上述函数,那么每个Thread都会执行functionExample这个函数。
Thread 有多少?
thread总数量= grid数量 * 一个grid里面的block数量 * 一个block里面的threads的数量
CUDA里面的Grid和Block作为线程组织的组织单位,一个Grid可包含N个Block,一个Block包含N个thread。
在C++代码中(主机运行代码中)调用CUDA的多线程函数,一般过程是标记函数、设置线程数、执行函数。这里放一个CUDA GUIDE里面的样例代码
__global__ void MatAdd(float A[N][N],float B[N][N],float C[N][N])
{
int i = blockIdx.x*blockDim.x + threadIdx.x;
int j = blockIdx.y*blockDim.y + threadIdx.y;
if (i<N && j<N)
c[i][j] =A[i][j] + B[i][j]
}
int main()
{
...
// Kernel invocation
dim3 threadsPerBlock(16,16); // 定义一个block里面多少个thread 16*16
dim3 numBlocks(N / threadsPerBlock.x, N / threadsPerBlock.y); //定义grid 里面有多少个Blck
MatAdd<<<numBlocks,threadsPerBlock>>>(A,B,C)
}
2.2 如何让不同的thread与需要计算的数据匹配
既然有这么多的Thread去计算相同块的数据,会不会重复或者漏算?现在的已知条件是:
- 一批GPU的Threads
- 一批待运算数据
我们需要做的是让数据与Thread对应起来。这里就涉及到了thread的编号
thread的一维索引的计算相对简单,一般:
int thID = threadIdx.x + blockIdx.x *blockDim.x;
计算示例如下,展示了获取第6个block里面的第5个thread的索引计算:
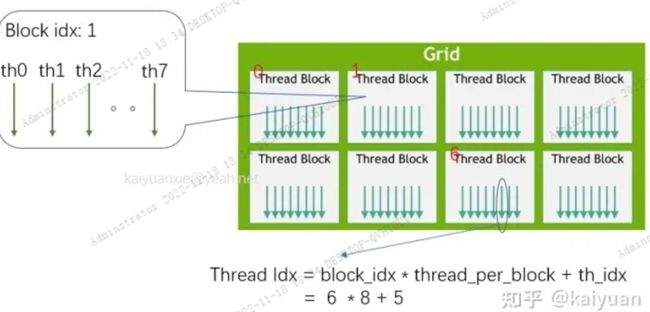
若对thread进行二维编号,那么每个thread的编号(索引)计算就需要多一个维度的编号。在前面MatAdd示例中展示的就是二维的thread索引计算:
int i = blockIdx.x * blockDim.x + threadIdx.x;
int j = blockIdx.y * blockDim.y + threadIdx.y
这样获得了这个thread的索引Idx,函数里面需要用户自行去确定索引与数据的对应关系。即,用户要根据Idx,自己分配thread与计算数据的映射关系。
2.3 代码的基本实现
根据矩阵运算CPU的代码,我们得到GPU运算的代码如下所示(详细源代码参看:MatMulKernel1D):
https://github.com/CalvinXKY/BasicCUDA/blob/master/matrix_multiply/matMul1DKernel.cu
__global__ void MatMulKernel1D(float *C, float *A,float *B, const int wh,const int wC, const int hC )
{
const int totalSize = wC *hC;
int thID = threadIdx.x +blockIdx.x * blockDim.x; //索引计算
while (thID < totalSize)
{
int Cx = thID / wC; // 数据坐标 与 thread 索引的映射
int Cy = thID % wC;
float rst = 0.0;
for (int i=0;i<wh; i++)
{
rst += A[Cx*wh+i]*B[i*wC +Cy];
}
C[Cx * wC +Cy] =rst;
thID += gridDim.x * blockDim.x;
}
}
相比CPU的code,主要的不同点:
- for 循环由三层变为一层(不算while循环);
- 增加了一个thread的索引计算
- 每个thread完成1个(或多个)C矩阵元素计算
- while循环是为了在总threads数量不等于C矩阵元素总数量时,防止"数据不足"或者访问越界。
2.4 共享内存优化计算
上述过程中我们已经实现了CUDA对矩阵的计算,为了进一步优化运算。需要使用一些加速手段,这里最常用的方式是使用共享内存。共享内存是一种片上内存,它的访问速度与L1相同。共享内存特点可参考显存理解。关键特点:
- 一个Block内的thread都能访问
- c++中通过
__shared__关键字定义
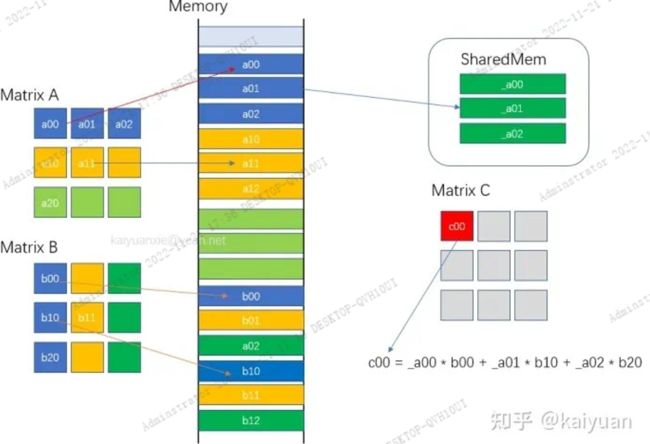
对于一些访问频率高的数据,可以从全局内存转移到共享内存中,这样能提升运算速度。在矩阵乘法中(C=A x B),要获得C矩阵的某一行(比如i行)数据,A矩阵中的i行数据需要与B矩阵的所有列数据都相乘一次。一般而言,数据都是在运算中从全局内存中加载到寄存器中,那么A矩阵的i行数据在本次运算中需要加载B的列次(假设B有K列)。如果有共享内存,我们只需要将该数据从全局内存加载一次到共享内存,然后再反复使用。数据传输方式由:
(Global memory ->L2 ->L1 -> register)*K*factor1
变为:
Global memory -> shared memory +(shared memory -> register)*K* factor2
所以每次运算,我们将A矩阵的i行放入到共享内存中,保证第i行数据不会反复从Global中加载,从而提升运算速度。函数代码片段如下:
template <int shWASize>
__global__ void MatMulKernel1DWithShMem(float *C,float *A, float *B,const int wA,const int wC,const int hC)
{
__shared__ float sRow[shWASize]: //定义贡献内存的大小
int blockID = blockIdx.x;
while(blockID <hC)
{
int thIdx = threadId.x;
while(thIdx < wA)
{
sRow[thIdx] = A[blockID * wA +thIdx];
thIdx +=blockDim.x;
}
__syncthreads();
thIdx = threadId.x;
while(thIdx < wC)
{
float sum = 0.0;
for (int i=0;i<wA;i++)
{
sum +=sRow[i]*B[wC*i +thIdx];
}
c[blockID * wC +thIdx]=sum;
thIdx += blockDim.x
}
blockID += gridDim.x;
}
}
源码:MatMulKernel1DWithShMem
需要注意的是,共享内存的大小是有限的,不同GPU的共享内存大小不一;其次,我们需要对共享内存里的值进行初始化,并且初始化后需要让block中的线程同步。关键内容如下:
// 使用while是用来保证thread的数量与矩阵A的宽度不相等时,数据多算或少算
while(thIdx < wA)
{
sRow[thIdx] = A[blockID * wA +thIdx];
thIdx +=blockDim.x;
}
__syncthreads(); //需要让线程同步,不然后面的运算可能出错
采用共享内存后,通过测试会发现,矩阵运算的时间不降反增。其实原因很简单,因为共享内存使用的成本高于其节约的时间。这样我们需要进一步优化,比如采用2D block并B配合共享内存。
3 二维块(2D Block)优化运算
3.1 运算实现
2D block 相比1D block,最大的差异是thread的编号由1维度变为2维。在矩阵乘法中,我们可以将矩阵拆分维子矩阵,让每个block对应计算一个子矩阵。如下图所示,我们计算C= A x B,如果只获得C中某个子矩阵Cs(假设Cs的大小为MM),只需要抽取A的M行数据,以及B的M列数据,进行运算。
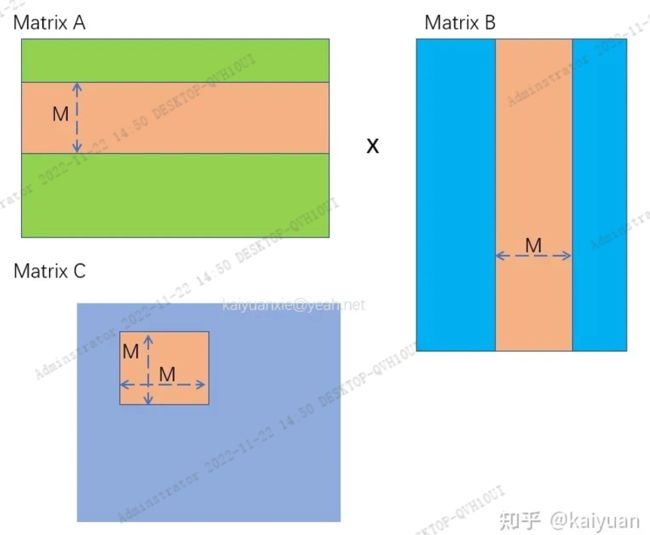
Cs矩阵的具体运算可拆解为:Cs=As0 x Bs0 +As1 x Bs1 + …+ Asm xAsm。如下图所示,我们用宽度为M的方块去分割数据。这样每个小矩阵的大小都是MM。那么,为什么要进行分割运算呢,直接运算不是很简洁?实际上就是为了使用共享内存,减少数据的加载次数。上面的运算中,例如:As0 x Bs0运算由于As0与Bs0可以足够小,都能加载到共享内存中,每个数据可减少M-1次内存读写。
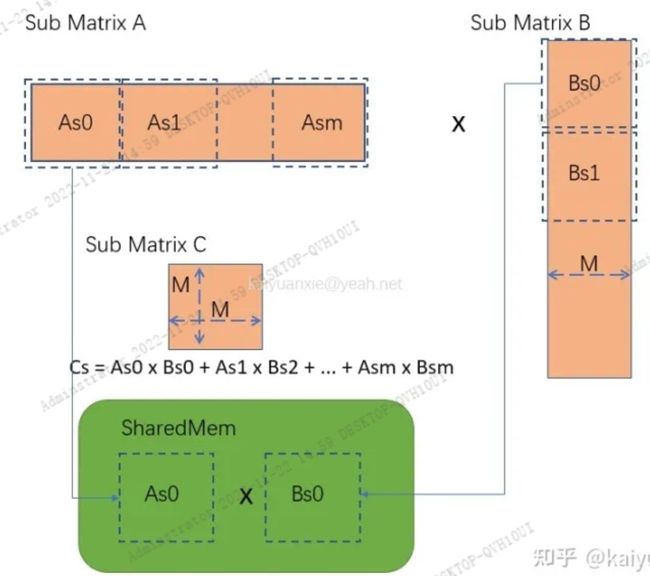
一般而言M*M设置的大小与CUDA中2D Block的大小一直,这样能够简化运算。
优化的代码关键如下:
template <int BLOCK_SIZE> __global__ void MatMulKernel2DBlockMultiplesSize(float *C, float *A, float *B, int wA, int wB)
{
// ... omit init ...
// Loop over all the sub-matrices of A and B
// required to compute the block sub-matrix
for (int a = aBegin, b = bBegin; a <= aEnd; a += aStep, b += bStep) {
// As与Bs 加载到共享内存中:
__shared__ float As[BLOCK_SIZE][BLOCK_SIZE];
__shared__ float Bs[BLOCK_SIZE][BLOCK_SIZE];
//让As Bs的数据初始化,从原始数据中映射:
As[ty][tx] = A[a + wA * ty + tx];
Bs[ty][tx] = B[b + wB * ty + tx];
// Synchronize to make sure the matrices are loaded
__syncthreads();
#pragma unroll
// 子矩阵的运算数据相加
for (int k = 0; k < BLOCK_SIZE; ++k) {
Csub += As[ty][k] * Bs[k][tx];
}
__syncthreads();
}
// Write the block sub-matrix to device memory;
// each thread writes one element
// 最终结果让汇总:
int c = wB * BLOCK_SIZE * by + BLOCK_SIZE * bx;
C[c + wB * ty + tx] = Csub;
}
源码:MatMulKernel2DBlockMultiplesSize
3.2 运算支持动态尺寸
在上述2D运算中,我们忽略了一个问题,就是运算矩阵的长宽有可能不能够被Block整除,如下所示:
示例1:矩阵宽度经过M整除后,最后一个行块的宽度小于M;
示例2:矩阵的高度经过M整除后,最后一个列快的高度小于M
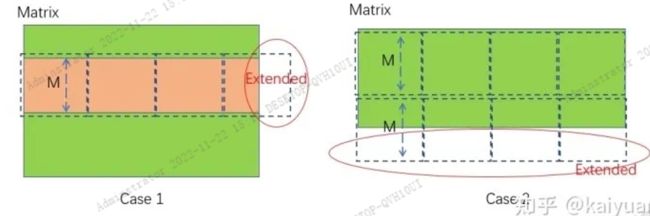
这样我们需要增加一些循环 + 条件判断来处理最后一个行块/最后一个列快的运算。
// ....
if (flag * BLOCK_SIZE + ty < wA || flag * BLOCK_SIZE + tx < wC) {
Bs[ty][tx] = B[b + wB * ty + tx];
} else {
Bs[ty][tx] = 0.0;
}
//....
if (BLOCK_SIZE * bx + tx < wC && BLOCK_SIZE * by + ty < hC) { // thread could over max.
C[wB * BLOCK_SIZE * by + BLOCK_SIZE * bx + wB * ty + tx] = Csub;
}
源码:MatMulKernel2DBlockMultiplesSize
3.3 CUBLAS函数调用
常用的矩阵运算,在CUDA的库CUBLAS中有现成的API函数。一般而言,它的运算方法比普通的优化运算要快,比如本例中的矩阵乘,可以调用cublasSgemm来运算。cublasSgemm调用非常方便。如下形式:
// ...
const float alpha = 1.0f;
const float beta = 0.0f;
cublasHandle_t handle;
checkCudaErrors(cublasCreate(&handle));
checkCudaErrors(cublasSgemm(
handle, CUBLAS_OP_N, CUBLAS_OP_N, dimsB.x, dimsA.y,
dimsA.x, &alpha, d_B, dimsB.x, d_A,
dimsA.x, &beta, d_C, dimsB.x));
// ...
checkCudaErrors(cublasDestroy(handle));
源码:matMulCublasKernel
但是不要过分迷信CUBLAS,毕竟它是个通用库,考虑的是通用性。对于一些特殊场景首先kernel有可能超过CUBLAS运算。
参考: https://zhuanlan.zhihu.com/p/573271688