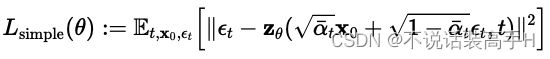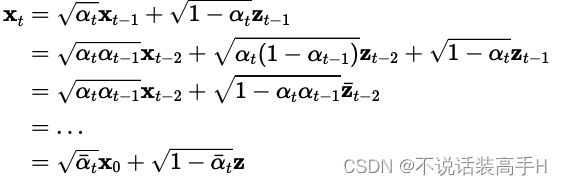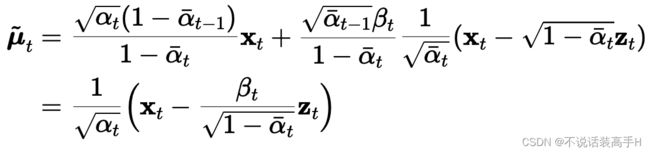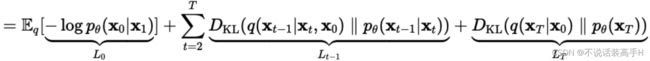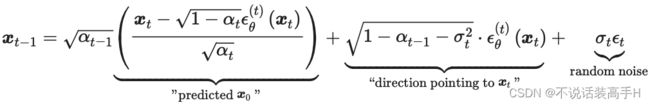Diffusion Model
DDPM
codebase 为 https://github.com/lucidrains/denoising-diffusion-pytorch
训练和推理流程如下:
Train
diffusion() ---> forward() ---> self.p_losses() 完成一个扩散阶段(包括前向计算和 BP),每次前向和 BP 中用到的 t(batch size 个)都是从 {1, 2, 3, ..., T} 中均匀采样得到的。
loss = diffusion(training_images) # training_images 为当前 batch 的输入图像
def forward(self, img, *args, **kwargs):
b, c, h, w, device, img_size, = *img.shape, img.device, self.image_size
assert h == img_size and w == img_size, f'height and width of image must be {img_size}'
t = torch.randint(0, self.num_timesteps, (b,), device=device).long()
img = normalize_to_neg_one_to_one(img)
return self.p_losses(img, t, *args, **kwargs) def p_losses(self, x_start, t, noise = None):
b, c, h, w = x_start.shape
noise = default(noise, lambda: torch.randn_like(x_start))
x = self.q_sample(x_start = x_start, t = t, noise = noise)
model_out = self.model(x, t)
target = noise
loss = self.loss_fn(model_out, target, reduction = 'none')
loss = reduce(loss, 'b ... -> b (...)', 'mean')
loss = loss * extract(self.p2_loss_weight, t, loss.shape)
return loss.mean()self.loss_fn() 为 L2 损失,对应论文中的:
self.q_sample() 输出的是由原图像 x0 和时间 t 计算出当前扩散采样点的 xt:
def q_sample(self, x_start, t, noise=None):
noise = default(noise, lambda: torch.randn_like(x_start))
return (
extract(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start +
extract(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape) * noise
)送入 U-Net ,之后再与 random noise z 计算损失,再之后梯度回传更新参数完成当前 iter 的训练。
Inference
diffusion.sample() ---> p_sample_loop() ---> self.p_sample() 完成一次采样:
sampled_images = diffusion.sample(batch_size = 4)
@torch.no_grad()
def sample(self, batch_size = 16):
image_size, channels = self.image_size, self.channels
sample_fn = self.p_sample_loop if not self.is_ddim_sampling else self.ddim_sample
return sample_fn((batch_size, channels, image_size, image_size))
@torch.no_grad()
def p_sample_loop(self, shape):
...
img = torch.randn(8, 3, 128, 128) # random noise
for t in tqdm(reversed(range(0, self.num_timesteps)), desc = 'sampling loop time step'):
img = self.p_sample(img, t)
return img
@torch.no_grad()
def p_sample(self, x, t: int, clip_denoised = True):
b, *_, device = *x.shape, x.device
batched_times = torch.full((x.shape[0],), t, device = x.device, dtype = torch.long)
model_mean, _, model_log_variance = self.p_mean_variance(x = x, t = batched_times, clip_denoised = clip_denoised)
noise = torch.randn_like(x) if t > 0 else 0. # no noise if t == 0
return model_mean + (0.5 * model_log_variance).exp() * noise最终 p_sample() 返回的是当前采样阶段得到的图像。
self.num_timesteps 是采样步数,DDPM 中推理时的采样步数与训练时的 T 保持一致。self.p_mean_variance() 预测当前采样步的均值和方差,DDPM 将方差设为超参数,故只需要预测均值:
def p_mean_variance(self, x, t, clip_denoised: bool):
preds = self.model_predictions(x, t)
x_start = preds.pred_x_start
if clip_denoised:
x_start.clamp_(-1., 1.)
model_mean, posterior_variance, posterior_log_variance = self.q_posterior(x_start = x_start, x_t = x, t = t)
return model_mean, posterior_variance, posterior_log_variance
U-Net 需要预测公式中的:
对应代码中的 model_predictions():
def model_predictions(self, x, t):
model_output = self.model(x, t) # theta
pred_noise = model_output #
x_start = self.predict_start_from_noise(x, t, model_output) # jun zhi
return ModelPrediction(pred_noise, x_start)
def predict_start_from_noise(self, x_t, t, noise):
return (
extract(self.sqrt_recip_alphas_cumprod, t, x_t.shape) * x_t -
extract(self.sqrt_recipm1_alphas_cumprod, t, x_t.shape) * noise
)最终输出的均值对应代码:
def q_posterior(self, x_start, x_t, t):
posterior_mean = (
extract(self.posterior_mean_coef1, t, x_t.shape) * x_start +
extract(self.posterior_mean_coef2, t, x_t.shape) * x_t
)
posterior_variance = extract(self.posterior_variance, t, x_t.shape)
posterior_log_variance_clipped = extract(self.posterior_log_variance_clipped, t, x_t.shape)
return posterior_mean, posterior_variance, posterior_log_variance_clippedDDIM
Train
diffusion() ---> forward() ---> self.p_losses()。除了 DDPM 中用到的损失外,在每个扩散阶段 DDIM 增加了一个损失,经过推导的 DDPM 优化目标的中间形式是最小化两个分布间的 KL 散度:
DDIM 的每个扩散阶段加入了这个 KL 散度损失。DDIM 的 self.p_losses() 为:
def p_losses(self, x_start, t, noise = None, clip_denoised = False):
noise = default(noise, lambda: torch.randn_like(x_start))
x_t = self.q_sample(x_start = x_start, t = t, noise = noise)
# model output
model_output = self.model(x_t, t)
# calculating kl loss for learned variance (interpolation)
true_mean, _, true_log_variance_clipped = self.q_posterior(x_start = x_start, x_t = x_t, t = t)
model_mean, _, model_log_variance = self.p_mean_variance(x = x_t, t = t, clip_denoised = clip_denoised, model_output = model_output)
# kl loss with detached model predicted mean, for stability reasons as in paper
detached_model_mean = model_mean.detach()
kl = normal_kl(true_mean, true_log_variance_clipped, detached_model_mean, model_log_variance)
kl = meanflat(kl) * NAT
decoder_nll = -discretized_gaussian_log_likelihood(x_start, means = detached_model_mean, log_scales = 0.5 * model_log_variance)
decoder_nll = meanflat(decoder_nll) * NAT
# at the first timestep return the decoder NLL, otherwise return KL(q(x_{t-1}|x_t,x_0) || p(x_{t-1}|x_t))
vb_losses = torch.where(t == 0, decoder_nll, kl)
# simple loss - predicting noise, x0, or x_prev
pred_noise, _ = model_output.chunk(2, dim = 1)
simple_losses = self.loss_fn(pred_noise, noise)
return simple_losses + vb_losses.mean() * self.vb_loss_weightInference
diffusion.sample() ---> self.ddim_sample()。
@torch.no_grad()
def ddim_sample(self, shape, clip_denoised = True):
batch, device, total_timesteps, sampling_timesteps, eta, objective = shape[0], self.betas.device, self.num_timesteps, self.sampling_timesteps, self.ddim_sampling_eta, self.objective
times = torch.linspace(0., total_timesteps, steps = sampling_timesteps + 2)[:-1]
times = list(reversed(times.int().tolist()))
time_pairs = list(zip(times[:-1], times[1:]))
img = torch.randn(shape, device = device)
for time, time_next in tqdm(time_pairs, desc = 'sampling loop time step'):
alpha = self.alphas_cumprod_prev[time]
alpha_next = self.alphas_cumprod_prev[time_next]
time_cond = torch.full((batch,), time, device = device, dtype = torch.long)
pred_noise, x_start, *_ = self.model_predictions(img, time_cond)
if clip_denoised:
x_start.clamp_(-1., 1.)
sigma = eta * ((1 - alpha / alpha_next) * (1 - alpha_next) / (1 - alpha)).sqrt()
c = ((1 - alpha_next) - sigma ** 2).sqrt()
noise = torch.randn_like(img) if time_next > 0 else 0.
img = x_start * alpha_next.sqrt() + \
c * pred_noise + \
sigma * noise
img = unnormalize_to_zero_to_one(img)
return img采样时用 Xt 计算出 Xt-1,self.model_predictions() 输出的 x_start 为下式中的 predicted x0 项。