深度学习汇总（四）

1 Batch Normalization(BN)原理

参考文章：https://blog.csdn.net/qq_37541097/article/details/104434557
目的：我们在图像预处理过程中通常会对图像进行标准化处理，这样能够加速网络的收敛

原理：

我们希望输入的所有训练数据样本满足某一分布规律，理论上是指所有的训练样本满足分布规律，而不是某一个样本满足。而Batch Normalization的目的就是使我们的feature map满足均值为0，方差为1的分布规律。
在实际的任务中，如果要计算机一下计算出所有样本的分布，显然是不可能的。所以我们针对模型喂入的batch图片数，计算一个batch的分布规律（batch越大越接近整个数据集的分布，效果越好）。对于图像$x$而言，图像是RGB三通道则有$x=(x^{(1)},x^{(2)},x^{(3)})$，分别对应三个通道的特征矩阵。
BN的计算公式如下：

我们根据上图的公式可以知道$\mu \beta$代表着我们计算的feature map每个维度（channel）的均值，注意$\mu \beta$是一个向量不是一个值，$\mu \beta$向量的每一个元素代表着一个维度（channel）的均值。${\sigma }_{\beta }^2$代表着我们计算的feature map每个维度（channel）的方差，注意${\sigma }_{\beta }^2$是一个向量而不是一个值，${\sigma }_{\beta }^2$向量的每一个元素代表着一个维度（channel）的方差，然后根据$\mu \beta$和${\sigma }_{\beta }^2$计算标准化处理后得到的值。下图给出了一个计算均值和方差的示例：

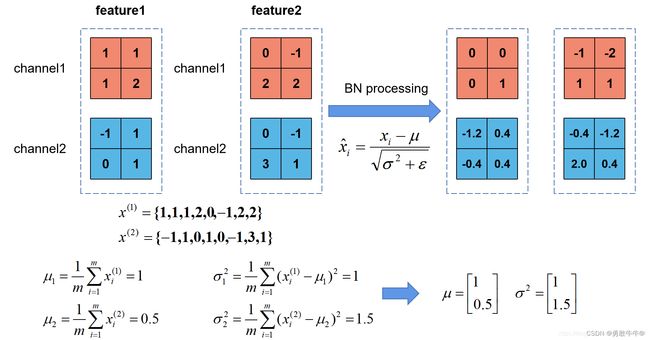
上图展示了一个batch size为2（两张图片）的Batch Normalization的计算过程，假设feature1、feature2分别是由image1、image2经过一系列卷积池化后得到的特征矩阵，feature的channel为2，那么$x^{(1)}$代表该batch的所有feature的channel1的数据，同理$x^{(2)}$代表该batch的所有feature的channel2的数据。然后分别计算$x^{(1)}$和$x^{(2)}$的均值与方差，得到我们的$\mu \beta$和${\sigma }_{\beta }^2$两个向量。然后在根据标准差计算公式分别计算每个channel的值（公式中的$ϵ$是一个很小的常量，防止分母为零的情况）。在我们训练网络的过程中，我们是通过一个batch一个batch的数据进行训练的，但是我们在预测过程中通常都是输入一张图片进行预测，此时batch size为1，如果在通过上述方法计算均值和方差就没有意义了。所以我们在训练过程中要去不断的计算每个batch的均值和方差，并使用移动平均(moving average)的方法记录统计的均值和方差，在训练完后我们可以近似认为所统计的均值和方差就等于整个训练集的均值和方差。然后在我们验证以及预测过程中，就使用统计得到的均值和方差进行标准化处理。
注：在BN的计算公式中还存在可训练参数$\gamma$和$\beta$。其中$\gamma$用来调整数值分布的方差大小，$\beta$用来调节数值均值的位置。这两个参数是在反向传播的过程中学习得到的，$\gamma$的默认值为1，$\beta$的默认值为0。

进阶知识：

以上的内容，对于一个batch一个batch的计算均值和方差，是在样本训练过程中，而我们在预测和验证过程中到底是怎么样的呢 ？以前的理解是对于某个任务，逐个batch求均值和方差，然后计算其统计量，顾名思义就是对若干batch得均值和方差再求均值，使其适用于决大多数的样本分布。但是真的是这样的吗，其实并不是：在我们的验证和测试过程中所使用的均值和方差是一个统计量${\mu }_{test}$和${\sigma }_{test}^2$。将训练阶段得到的$\mu \beta$均值记作${\mu }_{train}$，将${\sigma }_{\beta }^2$方差记作${\sigma }_{train}^2$，其中momentum默认取0.1，如下式所示：
$${\mu }_{test}+1=(1-momentum)\times {\mu }_{test}+momentum\times {\mu }_{train}$$
$${\sigma }_{test}^2+1=(1-momentum)\times {\sigma }_{test}^2+momentum\times {\sigma }_{train}^2$$
这里要注意一下，在pytorch中对当前批次feature进行BN处理使所使用的${\sigma }_{train}^2$是总体标准差，计算公式如下：
$${\sigma }_{train}^2=\frac{1}{m}\sum _{i=0}^m{(x_i-{\mu }_{train})}^2$$
在更新统计量${\sigma }_{test}^2$时采用的${\sigma }_{train}^2$是样本标准差，计算公式如下：
$${\sigma }_{train}^2=\frac{1}{m-1}\sum _{i=0}^m{(x_i-{\mu }_{train})}^2$$
（1）训练时要将traning参数设置为True，在验证时将trainning参数设置为False。在pytorch中可通过创建模型的model.train()和model.eval()方法控制。
（2）batch size尽可能设置大点，设置小后表现可能很糟糕，设置的越大求的均值和方差越接近整个训练集的均值和方差。
（3）建议将bn层放在卷积层（Conv）和激活层（例如Relu）之间，且卷积层不要使用偏置bias，因为没有用，参考下图推理，即使使用了偏置bias求出的结果也是一样的。

2 RoIPool & RoIAlign

参考文章：https://blog.csdn.net/qq_37541097/article/details/123754766

RoIPool

原理：

在Faster RCNN中，会使用RoIPool将RPN得到的Proposal（提议）池化到相同大小。这个过程会涉及quantization（量化）或者说取整操作，这会导致定位不是那么的准确（文中称为misalignment问题）。
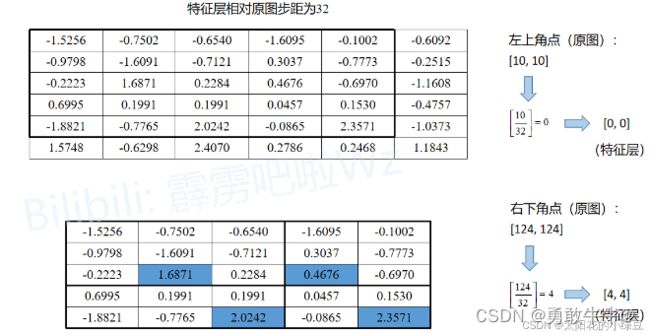
下面的示意图就是RoIPool的执行过程，其中会经历两次quantization。假设通过RPN得到了一个Proposal，它在原图上的左上角坐标是(10,10)，右下角的坐标是(124,124)，对应要映射的特征层相对原图的步距为32，通过RoIPool期望的输出为2x2大小：

• 将Proposal映射到特征层上，对于左上角坐标$\frac{10}{32}$四舍五入后等于0，对于右下角坐标$\frac{124}{32}$四舍五入后等于4，即映射在特征层上的左上角坐标为(0,0)，右下角坐标为(4,4)。对应下图特征层上从第0行到第4行，从第0列到第4列的区域（黑色矩形框）。这是第一次quantization。
• 由于期望的输出为2x2大小，所以需要将映射在特征层上的Proposal划分成2x2大小区域。但现在映射在特征层上的Proposal是5x5大小，无法均分，所以强行划分后有的区域大有的区域小，如下图所示。这是第二次quantization。
• 对划分后的每个子区域进行maxpool即可得到RoIPool的输出，即$⟮\begin{array}{cc}1.6871& 0.4676\\ 2.0242& 2.3571\end{array}⟯$。就得到了一个$2\times 2$大小的特征图。
  这里只是介绍一下RoIPool的概念，可以理解为感兴趣区域池化。

RoIAlign

原理：

由于RoIPool中，对于类似$5\times 5$的proposal区域进行池化，会产生不规则的区域用于池化输出，作者认为这种方式丢失了精确的空间定位信息。所以提出了RoIAlign。
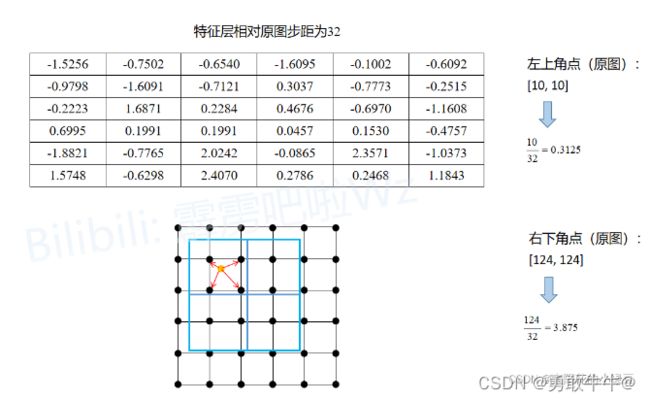
下面的示意图就是RoIAlign的执行过程。同样假设通过RPN得到了一个Proposal，它在原图上的左上角坐标是(10,10)，右下角的坐标是(124,124)，对应要映射的特征层相对原图的步距为32，通过RoIAlign期望的输出为2x2大小：

• 将Proposal映射到特征层上，左上角坐标$(0.3125,0.3125)$(不进行四舍五入)，右下角坐标$(3.875,3.875)$(不进行四舍五入)。为了方便理解，将特征层上的每个元素用一个点表示，就能得到图中下方的grid网格。图中蓝色的矩形框就是Proposal（没有quantization）。
• 由于期望输出为2x2大小，故将Proposal划分为2x2四个子区域（没有quantization）。接着根据sampling_ratio在每个子区域中设置采样点，原论文中默认设置的sampling_ratio为4，这里为了方便讲解将sampling_ratio设置成1。
• 然后计算每个子区域中每个采样点的值（利用双线性插值计算），最后对每个区域内的所有采样点取均值即为该子区域的输出。
  
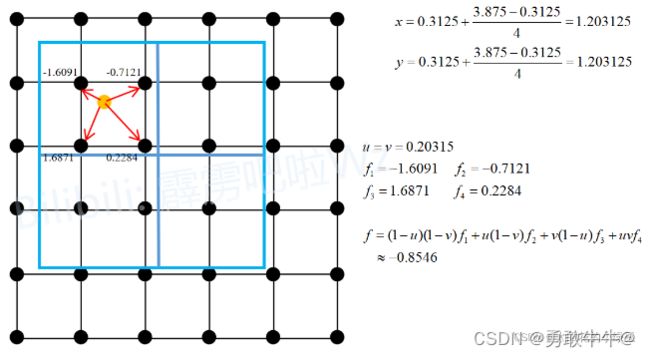
  这里以第一个子区域为例，因为这里将sampling_ratio设置成为1，所以每个子区域只需要设置一个采样点。第一个子区域的采样点为图中黄色的点（即为该子区域的中心点），坐标为$(1.203125,1.203125)$，然后找出离该采样点最近的四个点（即图中用红色箭头标出的四个黑点），然后利用双线性插值即可计算得到采样点对应的输出$-0.8546$。又由于该子区域只有一个采样点，故该子区域的输出就为$-0.8546$。
  

3 双线性插值

参考文章：https://blog.csdn.net/qq_37541097/article/details/112564822

线性插值

原理：

线性插值是指插值函数为一次多项式的插值方式。线性插值的几何意义即为利用过A点和B点的直线来近似表示原函数。线性插值可以用来近似代替原函数，也可以用来计算得到查表过程中表中没有的数值。
那么如下图所示，假设已知$y_1=f(x_1)$，$y_2=f(x_2)$ ，现在要通过线性插值的方式得到区间$[x_1,x_2]$内任何一点的$f(x)$值。

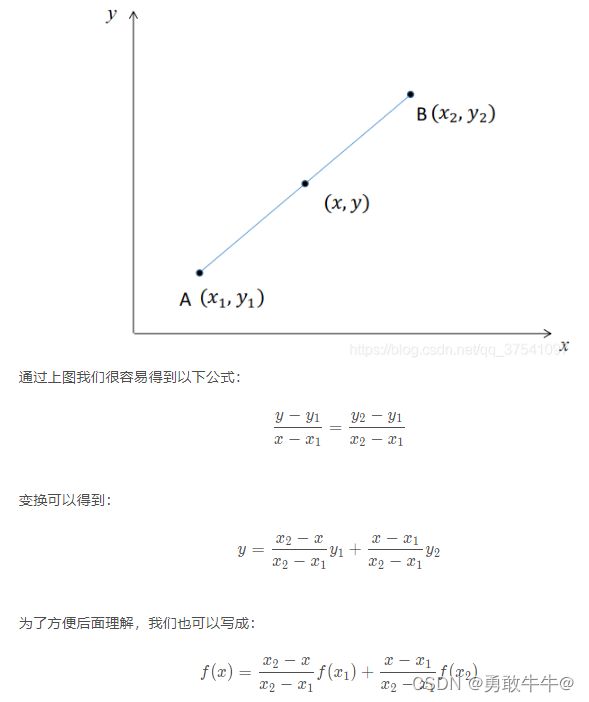
双线性插值

原理：

双线性插值，又称为双线性内插，在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。
通过以上介绍我们知道，双线性插值就是分别在两个方向上分别进行一次简单的线性插值即可。如下图所示，每个点的数值是由$z=f(x,y)$即$x,y$两个变量决定。下图可理解为沿z轴方向的俯视图。我们已知$Q_{11}、Q_{12}、Q_{21}、Q_{22}$四个点的值，现在要在$Q_{11}、Q_{12}、Q_{21}、Q_{22}$四个点中插入一个点$P$，并算出$P$点的值。

在求$P$点之前，首次根据线性插值的方法求得$R_1、R_2$的值。对于$R_1$点，我们可以根据$Q_{11}、Q_{21}$两个点的线性插值得到。而$Q_{11}、Q_{21}$两个点的$y$值是相同的，所以两点的连线可以只看做变量$x$的函数。

• 根据上面的线性插值函数，可以得到$R_1$点的线性插值为：
  $$f(x)=\frac{x_2-x}{x_2-x_1}\times f(x_1)+\frac{x-x_1}{x_2-x_1}\times f(x_2)$$
• 可以求得$R_1$点的值：
  $$f(R_1)=\frac{x_2-x}{x_2-x_1}\times f(Q_{11})+\frac{x-x_1}{x_2-x_1}\times f(Q_{21})$$
• 同理可以得到$R_2$点的值：
  $$f(R_2)=\frac{x_2-x}{x_2-x_1}\times f(Q_{12})+\frac{x-x_1}{x_2-x_1}\times f(Q_{22})$$
  得到$R_1$和$R_2$的值以后，我们根据这两点，利用线性插值去计算最终的$P$点的值。$R_1$和$R_2$两个点的$x$值是相同的，所以两点的连线可看做只关于$y$一个变量的函数。通过线性插值公式可以得到：
  $$f(P)=\frac{y_2-y}{y_2-y_1}\times f(R_1)+\frac{y-y_1}{y_2-y_1}\times f(R_2)$$
• 代入$f(R_1)、f(R_2)$后得到：
  $$f(P)=\frac{(x_2-x)(y_2-y)}{(x_2-x_1)(y_2-y_1)}\times f(Q_{11})+\frac{(x-x_1)(y_2-y)}{(x_2-x_1)(y_2-y_1)}\times f(Q_{21})+\frac{(x_2-x)(y-y_1)}{(x_2-x_1)(y_2-y_1)}\times f(Q_{12})+\frac{(x-x_1)(y-y_1)}{(x_2-x_1)(y_2-y_1)}\times f(Q_{22})$$

图像中的双线性插值

原理：

在图像处理中，常见的坐标系如下图所示，以图像左上角为坐标原点，水平向右为x轴正方向，竖直向下为y轴正方向。注意像素值是从$(0,0)$点开始，假设我们在图像中插入一个点$P$，离$P$点最近的相邻四个像素点是$Q_{11},Q_{12},Q_{21},Q_{22}$，并利用双线性插值的方法求其值。
在图像中，像素点都是行列排序，如果插入一点，取其相邻像素的四个点，这四个点在排列组合上可能存在同行或者同列，也就是相隔一个像素取一个值。所以也就是取的四个点，相邻点之间的像素间隔为1个像素。所以该公式在图像区域内也是同理。
​$$f(P)=\frac{(x_2-x)(y_2-y)}{(x_2-x_1)(y_2-y_1)}\times f(Q_{11})+\frac{(x-x_1)(y_2-y)}{(x_2-x_1)(y_2-y_1)}\times f(Q_{21})+\frac{(x_2-x)(y-y_1)}{(x_2-x_1)(y_2-y_1)}\times f(Q_{12})+\frac{(x-x_1)(y-y_1)}{(x_2-x_1)(y_2-y_1)}\times f(Q_{22})$$

• 在图像像素中进行插值某个点，然后取其周围详尽的四个点，这四个点一定在像素格点上，所以有$x_2-x_1=1，y_2-y_1=1$。代入上面的公式进一步化简可以得到：
  $$f(P)=(x_2-x)(y_2-y)\times f(Q_{11})+(x-x_1)(y_2-y)\times f(Q_{21})+(x_2-x)(y-y_1)\times f(Q_{12})+(x-x_1)(y-y_1)\times f(Q_{22})$$
• 我们另：$x-x_1=\mu$，$y-y-1=\nu$其中$X$为插入点$p$的横坐标值，$y$为插入点$p$的纵坐标值。
• 代入公式可得：
  $$f(P)=(1-\mu )(1-\nu )\times f(Q_{11})+\mu (1-\nu )\times f(Q_{21})+(1-\mu )\nu \times f(Q_{12})+\mu \nu \times f(Q_{22})$$

4 Faster Rcnn(RPN生成锚框)

RPN的全称是$regionproposalnetwork$---->候选检测框生成网络
RPN网络的输入是：backbone输出得到的多尺度$featuremaps$。
RPN网络的输出是：$proposals$候选区域。
推理第一阶段先找出图片中待检测物体的anchor矩形框（对背景、待检测物体进行二分类），第二阶段对anchor框内待检测物体进行分类。

• RPN结构图如下：
  
  这里的一个问题是：区域候选框是如何生成的？
  解答：在浏览过其他人对Faster Rcnn网络论文的解读，初步的想法是RPN网络生成候选检测框。

Rcnn简述

Rcnn算法流程可分为4个步骤

• 1 一张图像生成1K~2K个候选区域（使用Selective Search方法）
• 2 对每个候选区域，使用深层网络提取特征（是将2K个候选区域送入深度网络）
• 3 将提取后的特征送入每一类的SVM分类器，判别是否属于该类别
• 4 使用回归器精细修正候选框的位置
  Fast Rcnn算法流程可分为3个步骤
• 1 一张图像生成1K~2K个候选区域（使用Selective Search方法）（候选框：原图上生成的候选区域）
• 2 将原图输入深度网络得到相应的特征图，然后将SS算法生成的候选框投影到特征图上获得相应的特征矩阵
• 3 将每个特征矩阵通过ROI Pooling层缩放到$7\times 7$大小的特征图，接着将特征图展平通过一系列全连接层得到预测结果
  针对步骤2 详解：Fast Rcnn将整张图像送入网络，紧接着从特征图像上提取相应的候选区域（是将原图上生成的候选区域通过下采样倍数关系以及框位置信息映射在特征图上，此时也就是将原图上生成的候选区域框映射在了特征图上），这些候选区域的特征不需要再重复计算。
  训练过程中，并不是使用每张图上的2K的样本，而是选择其中的一小部分参与模型的训练。候选框与真实框的iou大于0.5就认为是正样本，iou在[0.1~0.5）之间的样本被认为是负样本。
  Faster Rcnn算法流程可分为3个步骤
• 1 直接将图像输入进深度网络得到相应的特征图
• 2 使用RPN结构生成候选框，将RPN生成的候选框投影到特征图上获得相应的特征矩阵（这里不在使用SS算法生成候选区域，而是通过RPN结构生成候选框，然后将候选框投影到深度网络获得的特征图上）
• 3 将每个特征矩阵通过RoI Pooling层缩放到$7\times 7$大小的特征图，接着讲特征图展平通过一系列全连接层得到预测结果
  针对步骤2 详解：RPN（Region Proposal Network）
  RPN的输入是深度网络生成的特征图，再特征图上通过$3\times 3$的滑动窗口获得K个anchor，这里具体来说就是每个滑动窗口的像素中心点都会生成9个anchor，概括的来讲呢，因为滑动窗口是针对于整个特征图而言的，故滑动窗口的每个中心点其实也就是特征图上的每个像素位置生成9个anchor。这9个anchor具有三种维度，每个维度又有三个不同尺度。比如一张$1000\times 600\times 3$的图像，其特征图如果是$60\times 40$则有$60\times 40\times 9$个anchor。对于RPN生成的候选框之间存在大量的重叠，基于候选框的cls得分，采用非极大值抑制，IoU设为0.7，这样每张图片上大概就剩2K个候选框。值得注意的是：K个候选框生成2K个分数信息，分别为前景概率分数和检测目标的概率分数，还生成4K个位置信息。
  训练过程中会在每张图上选择256个样本（是在每张图2K个候选样本中选择256个），其中正负样本比例为1:1，也即正样本128个，负样本128个。如果正样本不足128个，则会将负样本中IoU靠前的样本分给正样本。

5 损失函数

均方误差MSE(Mean Square Error,MSE)

参考文章：https://www.cnblogs.com/wangguchangqing/p/12021638.html

原理：

均方误差是模型预测输出值$f(x)$与模型真实标签值$y$之间差值的平方的的均值，其公式如下：
$$MSE=\frac{{\sum }_{i=1}^n(f_{x_i}-y_i{)}^2}{n}$$
其中，$y_i$和$f(x_i)$分别表示第$i$个样本的真实标签及其对应的预测输出值。当真实标签和预测输出的差值大于1时，他们的平方将会更大，则当差值小于1时，他们的平方会更小。$MSE$对于较大的误差(>1)给予较大的惩罚，较小的误差(<1)给予较小的惩罚。我们多次训练降低我们的损失函数（$MSE$）值时，那些相较于真实标签差距大的预测点，我们会更加关注，其对损失函数的影响以及贡献也就越大。
注意：还需要知道的是，$MSE$在图像化表示上为一个凹曲线，凹点为0原点。这也就是说，$MSE$的函数曲线光滑、连续、处处可导，在使用梯度下降法（梯度下降法是优化器），在优化的过程中，随着误差的减小，梯度也在减小，利于优化。
图像化表示：

均值绝对差MAE(Mean Absolute Error,MAE)

原理：

均值绝对差是指模型预测输出值$f(x)$与真实标签$y$之间差值绝对值的均值，其可以表示为：
$$MAE=\frac{{\sum }_{i=1}^n|f(x_i)-y_i|}{n}$$
其图形化表示如下;

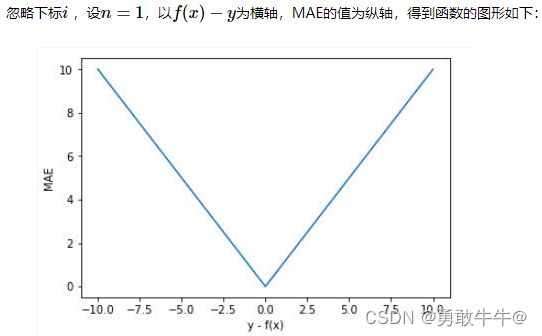
MAE曲线连续，但是在$y-f(x)=0$处不可导。而且 MAE 大部分情况下梯度都是相等的，这意味着即使对于小的损失值，其梯度也是大的，这不利于函数的收敛和模型的学习。但是，无论对于什么样的输入值，都有着稳定的梯度，不会导致梯度爆炸问题，具有较为稳健性的解。
由于MAE对于大部分情况的梯度都相等，所以对于离群点（与真实标签相差较大的点）也不是很敏感，也可以说对于任意大小位置的预测点，其惩罚力度都是一样的，损失函数对所有点的关注相同。

总结：

总的说各有利弊，对于一些异常值（离群点）毕竟是样本中的个别，所以对于异常点的学习好像又没什么必要，但是MAE导数不连续。而针对MSE损失函数，其容易受异常点（离群点）点的影响，我们可设置阈值将异常点的导数设置为0来避免这种情况（这里要说的就是：对于离群点，在MSE图像化中可以发现，其差值越大，其梯度越大）。

$smoot{h}_{L_1}$损失函数

原理：

公式如下;
$$Smooth{L}_1(x)=\{\begin{array}{ll}0.5x^2,& if|x|<1\\ |x|-0.5,& |x|>=1\end{array}$$
上式中，$L_1(x)=x=f(x_i)-y_i$为预测值与真实值的差值。
$Smooth{L}_1$能从两个方面限制梯度：

• 1 当预测值与真实标签值差别过大时，梯度为$|x|-0.5$两者差值的绝对值减0.5，不至于过大。
• 2 当预测值与真实标签值差别很小时（绝对值小于1），其对应的梯度值也足够小。
  下面对$L_1(x)$与$Smooth{L}_1(x)$求导可得：
  $$\frac{d{L}_1(x)}{dx}=\{\begin{array}{ll}1,& ifx>=0\\ -1,& x<0\end{array}$$
  $$\frac{dSmooth{L}_1(x)}{dx}=\{\begin{array}{ll}x,& if|x|<1\\ +-1,& |x|>=1\end{array}$$
• 1 L1对x的导数为常数，在训练的后期，预测值与ground truth差异很小时，L1的导数的绝对值仍然为1，而 learning rate 如果不变，损失函数将在稳定值附近波动，难以继续收敛以达到更高精度。
• 2 Smotth L1在x较小时，对x的梯度也会变小。 而当x较大时，对x的梯度的上限为1，也不会太大以至于破坏网络参数。
  注意:
  $L_2(x)=x^2$，对$L_2(x)$求偏导得：$\frac{d{L}_2(x)}{dx}=2x$
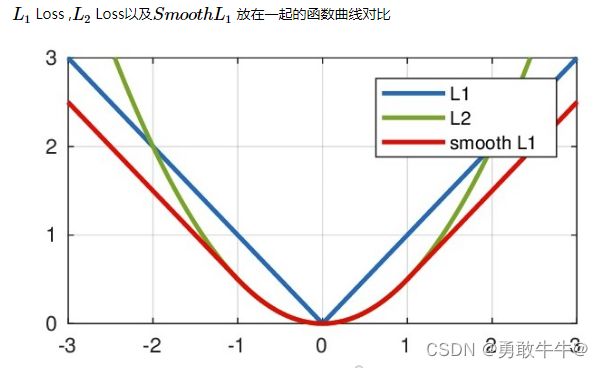
  Smooth L1的优点
  相比于L1损失函数，可以收敛得更快。
  相比于L2损失函数，对离群点、异常值不敏感，梯度变化相对更小，训练时不容易跑飞。
  三种损失函数图形化表示：
  

交叉熵损失函数

原理：

参考文章： https://zhuanlan.zhihu.com/p/38241764
正文： 交叉熵主要是用来判定实际的输出与期望的输出的接近程度
信息量：它是用来衡量一个事件的不确定性的；一个事件发生的概率越大，不确定性越小，则它所携带的信息量就越小。
熵：它是用来衡量一个系统的混乱程度的，代表一个系统中信息量的总和；信息量总和越大，表明这个系统不确定性就越大。
交叉熵：主要刻画的是实际输出（概率）与期望输出（概率）的距离，交叉熵的值越小，两个概率分布就越接近。假设概率分布$\hat{y}$为预测输出（则为真实标签为0或1时，其对应的概率），概率分布$y$为期望输出（$y$可以认为是一个样本的真实标签：0或者1），$L$为交叉熵，对于（单个样本的损失函数）二分类问题的表达式为：
$$L=-[ylog\hat{y}+(1-y)log(1-\hat{y})]$$
在二分类问题中，如果某样本的真实标签为1（$y=1$），则交叉熵公式为：$L=-log\hat{y}$，这时，其图像化表示为：

从上图可以发现，对于真实标签为1的样本，其交叉熵函数为$L=-log\hat{y}$，也就是预测输出$\hat{y}$越接近真实标签的值1，则交叉熵函数损失越小。同理，当真实标签为0时，只有期望输出值$\hat{y}$越接近0，则损失函数才会越小。
如果是计算N个样本的总的损失函数，则表达式为：
$$L=-\sum _{i=1}^N{y}^{i}log\widehat{y^i}+(1-y^i)log(1-\widehat{y^i})$$
对于多样本的情况，也是同理，在真实标签$y^i$的情况下，将期望输出$\widehat{y^i}$的概率无限逼近真实标签，则就有了多样本的交叉熵损失函数。

$Focal-Loss$损失函数

原理：

论文提出影响一阶段检测网络精度的原因在于：

• 1 正负样本对损失的影响
• 2 易分类样本与难分类样本对损失的影响
  
  Focal Loss具有两个重要的特点
• 1 控制正负样本的权重
• 2 控制容易分类和难分类样本的权重
  正负样本的概念如下：
  一张图像可能生成成千上万的候选框，但是其中只有很少一部分是包含目标的的，我们通过设定候选框与真实框的IoU的阈值（两个阈值）来划分正负样本。大于这一阈值的候选框都作为正样本，在两个阈值之间的样本直接丢弃，小于另一阈值的候选框则为负样本。
  容易分类和难分类的样本概念如下：
  从字面的意义来看，是针对候选框的样本属于哪一类别问题，假设对于一个二分类问题，其中A被认为是猫的概率是0.8，样本B被认为是猫的概率是0.65，则样本A有更大的可能被认为就是猫，而B认为是猫的可能性则缩小，掺杂了更多的不确定性。所以A就被人为是易分类样本，而B被认为是难分类样本。
  由上面的交叉熵损失函数我们可得：
  $$L=-[ylog\hat{y}+(1-y)log(1-\hat{y})]=\{\begin{array}{ll}-log\hat{y},& ify=1\\ -log(1-\hat{y}),& y=0\end{array}$$
  想要降低负样本的影响，可以在常规的损失函数前增加一个系数αt。与Pt类似，当label=1的时候，αt=α；当label=otherwise的时候，αt=1 - α，a的范围也是0到1。此时我们便可以通过设置α实现控制正负样本对loss的贡献。
• 控制正负样本的权重
  $$L=\{\begin{array}{ll}-\alpha log\hat{y},& ify=1\\ -(1-\alpha )log(1-\hat{y}),& y=0\end{array}$$
  按照A、B样本分类的例子，A被认为是猫的概率是0.8，样本B被认为是猫的概率是0.65，则A被认为是易分类样本，而B认为是难分类样本。也就是样本的分类概率越大，越容易进行分类，利用$1-P_t$就可以计算出样本属于容易分类样本还是难分类样本。
• 控制易分类样本和难分类样本的权重
  其中$1-P_t$为：$P_t=\{\begin{array}{ll}p,& ify=1\\ 1-p,& y=0\end{array}$，$p$就是当样本的真实标签为1或者0使，模型的预测输出概率。$p$大，就说模型预测输出的这个样本为易分类样本，$p$小，就说模型预测输出的这个样本为难分类样本。
  调制系数：$(1-P_t{)}^{\gamma }$为易分类样本和难分类样本的调制系数。
• 1 当$P_t$趋于0的时候，调制系数趋于1，对于总的loss的贡献很大。当$P_t$趋于1的时候，调制系数趋于0，也就是对于总的loss的贡献很小。
• 2 当$\gamma =0$的时候，focal loss就是传统的交叉熵损失，可以通过调整γ实现调制系数的改变

则最终的$FocalLoss$损失函数可以表达为：
$$F_L(\hat{y})=\{\begin{array}{ll}-\alpha (1-\hat{y}{)}^{\gamma }log\hat{y},& ify=1\\ -(1-\alpha ){\hat{y}}^{\gamma }log(1-\hat{y}),& y=0\end{array}$$
另一种写法：
$$F_L(P_t)=-{\alpha }_t(1-P_t{)}^{\gamma }log(P_t)$$

6 如何理解“梯度下降法”？什么是“反向传播”？

参考文章：https://zhuanlan.zhihu.com/p/66534632

原理：

梯度下降法就是反向传播的一种方式。
梯度下降法可以理解为针对于损失函数的优化算法，为什么这么说呢？在模型进行训练的过程中，模型读入一个batch，两个，以及更多，直到所有的迭代次数完成，模型只是针对于你设定的epoch数完成了训练，得到一堆大得离谱的损失值，为什么呢，因为没有参数更新，得不到最优的参数，而得到最优的参数仅仅是参数更新吗，也不是。这就有了优化器的作用，他会辅助损失函数进行梯度回传，然后进行参数的更新，以保证损失值越来越小，也就是模型在向着最优解逐步靠近。
参数更新：
参数的更新对象其实就是$W$和$b$，对于$Wx+b$来说，$dW$就是输入值乘以$x$，$db$就等于输入值。这里用$dW$和$db$表示反向传播到$W$和$b$节点时的计算结果。
那现在该怎样更新W和b呢？

• 其一，需要引入正则化惩罚项。这是为了避免最后求出的W过于集中所设置的项，比如$[1/3,1/3,1/3]$和$[1,0,0]$，这两个结果明显前一个结果更为分散，也是我们更想要的。为了衡量分散度，我们用$\frac{1}{2W^2}$来表示。对该式求导，结果就是W。设正则化惩罚项的系数值为$reg$，那么修正后的$dW$可以写为：
  $$dW=dW+reg\times W$$
• 其二，是步子迈的有点大。直接反向传播回来的量值可能会比较大，在寻找最优解的过程中可能会直接将最优解越过去，所以在这里设置一个参数：学习率。我们将学习率用epsilon表示，那么最终更新后的W和b写为：
  $$W=W-epsilon\times dW=W-\eta \times dW$$
  $$b=b-epsilon\times db=b-\eta \times db$$
  至此，一次反向传播的流程就走完了。
  加法节点反向传播示意图：
  
  乘法节点反向传播示意图：
  
  注：一部分是看的别人的，再根据自己的理解进行升华，参考的文章已经表明出处，感谢每个人无私的付出❤