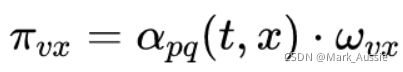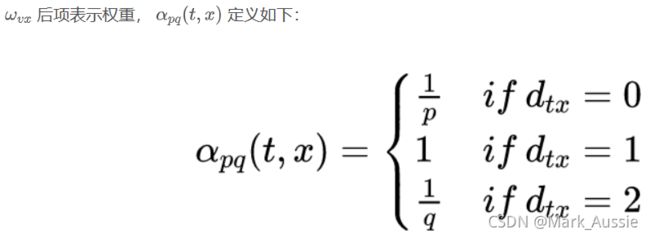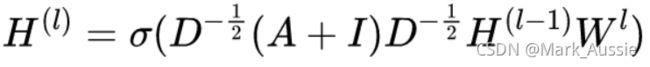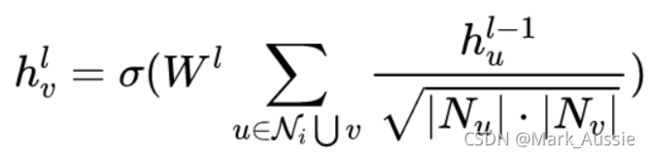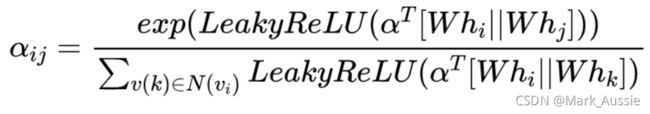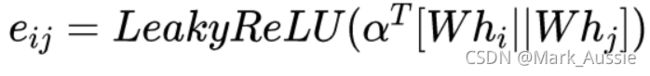图表示学习
图表示学习的主要目标，正是将图数据转化成低维稠密的向量化表示方式，同时确保图数据的性质在向量空间中也能够得到对应。图数据的表示，可以是节点层面，或是全图层面，节点(图数据的基本元素)的表示学习一直是图表示学习的主要对象。图数据的表示如果能含有丰富的语义信息，就能得到好的输入特征，直接选用线性分类器对分类任务学习。
图表示学习的主要目标：将结点映射为向量表示，尽可能多地保留图的拓扑信息。
主要分为基于图结构的表示学习和基于图特征的表示学习。
基于图结构的表示学习对结点的向量表示只来源于图的拓扑结构，缺乏对图结点特征消息的表示。
基于图特征的表示学习对结点的向量表示既包含了图的拓扑信息也包含了已有的特征向量。
基于图结构的表示学习
图表示学习的任务就是用 n 个向量表示图上的 n 个结点，这样可将拓扑结构转化为向量。
在图表示学习中，在图上“接近”时向量空间也“接近”。对于第 2 个“接近”就是欧式空间两个向量的距离。对于第一个“接近”有多种解释如下：
-
1-hop：两个相邻的结点就可以定义为临近；
-
k-hop：两个 k 阶临近的结点也可以定义为临近；
-
具有结构性：结构性相对于异质性而言，异质性关注的是结点的邻接关系；结构性将两个结构上相似的结点定义为“临近”。如两个点是各自小组中心，这两个节点就具有结构性。
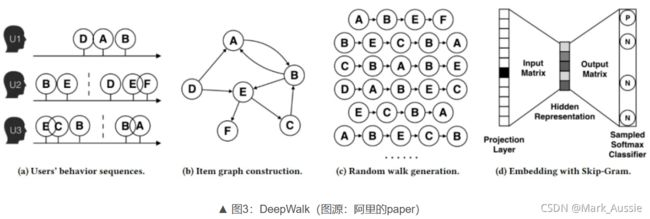
DeepWalk：采用 Random walk 进行结点采样。
如下图；根据用户的行为构建图网络；通过 Random walk 随机采样的方式构建出结点序列（如：开始在 A 点，A->B，B 又跳到邻居点 E，最后到 F，得到"A->B->E->F"序列）；序列问题就是 NLP 中的语言模型，句子就是单词构成的序列。之后是 Word2vec（词用向量表示）的问题，可采用 Skip-gram 模型得到最终的结点向量；这样就将图结构转化为序列问题。
注：结点走向其邻居结点的概率是均等的。在有向图和无向图中，游走方式不一样。
无向图中的游走方式是相连即可走；而有向图中则是只沿着“出边”的方向走。
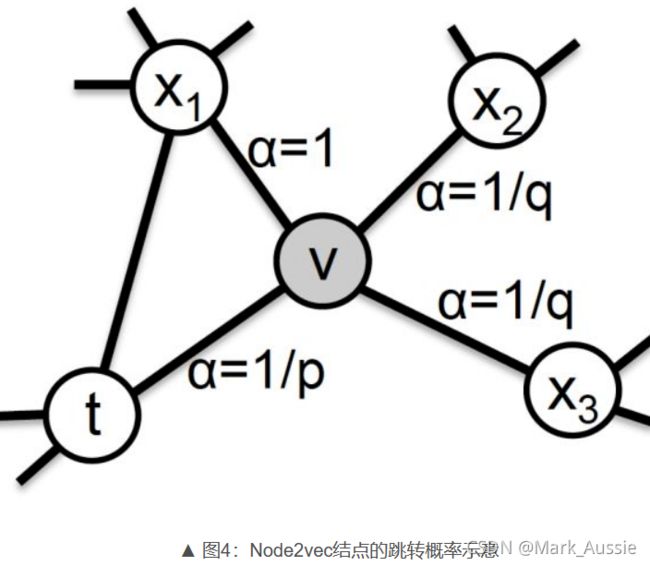
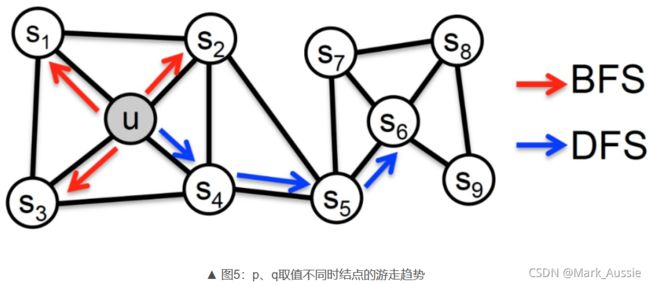
Node2Vec：Random Walk 中，一个结点向邻居结点游走的概率是相等的，这个假设与显示并不一定吻合；Node2vec 就是对结点间游走概率的定义。如下图，结点 t 跳跃到结点 v 之后，算法下一步从结点 v 向邻居结点跳跃的概率是不同的。
跳转概率公式(需要再做归一化才是转化的概率)：
从结点 v 回跳到上一个结点 t 的 α 为 1/p；
从结点 v 跳到 t、v 的公共邻居结点的 α 为 1；
从结点v跳到其他邻居的 α 为 1 / q;
用上述方法，就可以获得节点间的跳转概率。当 p 比较小的时候，结点间的跳转类似于 BFS(广度搜索)，结点间的“接近”就可以理解为结点在邻接关系上“接近”；当 q 比较小的时候，结点间的跳转类似于 DFS(深度搜索)，节点间的“接近”就可以视作是结构上相似。
基于图特征的表示学习
基于图特征的表示学习加入了结点的特征矩阵 X （姓名、年龄、身高等特征），为区别于基于图结构的表示学习，将这类的模型叫做“图神经网络”。
GCN：Graph Convolutional Networks（图卷积网络），新特征是对上一层邻居结点特征的聚合。
A 为邻接矩阵，D 是定点的度矩阵（对角矩阵），I 是单位矩阵，W 是神经网络间的系数矩阵；
H 代表层节点特征矩阵，第一层的特征矩阵为H0，就是原始节点特征举证 X(如上)。
上面的公式也可转为：
h(lv) 代表第 l 层中节点 v 的向量，h(l-1v) 代表的是 l 层上一层中节点u的向量，
Ni为几点i 的邻居节点集合；CGN 代表邻居节点的聚合。
GraphSAGE：采用了 固定的采样倍率和不同的聚合方式。
GCN 的聚合方式是将一个结点的所有邻居节点聚合。若每层结点的平均邻居结点个数为 
，K 层聚合后的结点聚合代价为 
，这样的计算量会很大。
GraphSAGE 在一个 epoch 中不适用某个结点所有邻居结点聚合，而是设置一个定值 Sk，在第 k 层选择邻居的时候只从中选最多选择 Sk 个邻居结点进行聚合，计算的复杂度大致在 
结点聚合应该满足：
-
对聚合结点的数量自适应：向量的维度不应随邻居结点和总结点个数改变。
-
聚合操作对聚合结点具有排列不变性。
-
显然，在优化过程中，模型的计算要是可导的。
集中聚合方式：
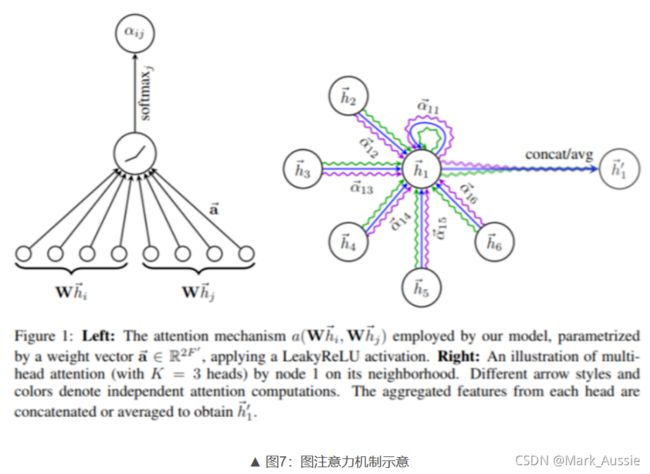
GAT：引入注意力机制的 GNN
aij 是 vi 与邻居节点 vj 的权重系数
相关度权重系数 eij计算公式如下，再对eij 做 softmax归一化。
上图右边是多头注意力机制，不同的颜色代表了不同的注意力计算过程，将结果进行拼接或平均。
计算公式如下：
参考：https://blog.csdn.net/c9Yv2cf9I06K2A9E/article/details/106393794
https://zhuanlan.zhihu.com/p/113235806