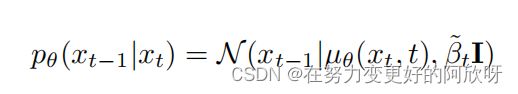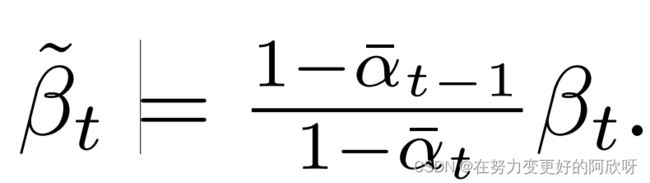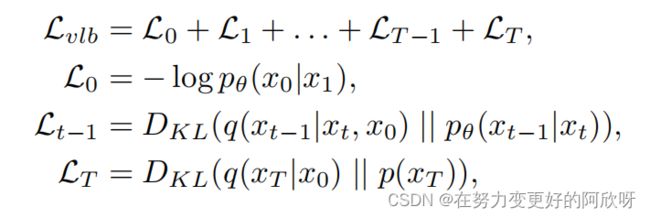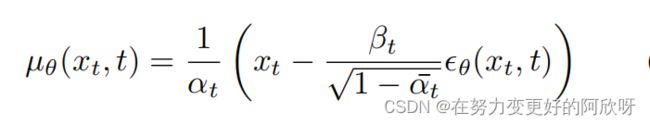AnoDDPM: Anomaly Detection with Denoising DiffusionProbabilistic Models using Simplex Noise论文学习

摘要

1.在基于重建的异常检测中，不需要全长马尔可夫链扩散。这导致我们开发了一种新的部分扩散异常检测策略，可扩展到高分辨率图像，名为AnoDDPM。

2.高斯扩散不能捕获较大的异常,因此，我们开发了一个多尺度的单纯形噪声扩散过程来控制目标异常大小。

一、介绍

1.DDPM能够从复杂的数据分布中生成样本，比GANs和VAEs具有更好的模式覆盖。去噪过程是从一个N(0,I)分布中获取样本，并随机地将其转换为一个学习到的数据分布。我们利用这一能力，构建了一个基于纯健康患者数据的模型AnoDDPM，该模型通过部分扩散过程将潜在的异常查询数据映射到健康分布上。然后，我们可以通过与原始图像进行比较来突出显示异常情况。部分扩散允许更好地重建样本从数据分布和规模到高分辨率图像良好。与完全扩散相比，较短的马尔可夫链会导致更快的推理和训练。

2.几种使用生成模型进行无监督异常检测的方法，如GANs和VAEs，已经被探索过。通常，模型学习从异常数据中生成非异常数据（健康的）图像或感兴趣的区域。通过确认异常是否位于学习表示流形之外，或者通过在像素空间中比较生成的图像和原始图像来检测异常。AnoGAN，用于异常检测的第一GAN之一，基于测试图像和迭代细化生成器近似之间的像素空间和鉴别器特征的差异对图像进行评分。细化过程需要数百次反向传播迭代，从而导致推理速度较慢。对AnoGAN的变体已经被提出，如f-AnoGAN和P-AnoGAN。f-AnoGAN利用一个Wasserstein GAN和一个编码器将查询映射到潜在空间中，以加快模型的速度。而PAnoGAN则使用渐进式GAN来提高可以检测到异常的分辨率。其他方法，如Zimmerer等人利用上下文编码器对图像进行绘制重建，Nguyen 等人利用超像素网络检测重建后的异常，因为训练和图像生成在较大的样本上会变得不稳定。

3.本文提出了一种新的异常检测方法，利用DDPMs来破坏图像，重建一个健康的近似。与对抗性训练相比，这有几个优点，因为它可以更好的捕获更小的数据集，并更好的提高样本质量和稳定的训练。然而，这种方法也面临着独特的挑战。正如我们将演示的，简单的高斯分布腐败可能不足以进行异常检测。作为一种补救方法，我们研究了单纯形噪声——计算机图形学中流行的方法，而不是高斯噪声。

综上所述，本文的主要贡献是:

1.一种部分扩散策略将异常图像噪声到一些参数化的时间步长λ，由变体重建，如图1. 

 2.利用多尺度单纯形噪声，使更大的异常区域被重建为健康区域。

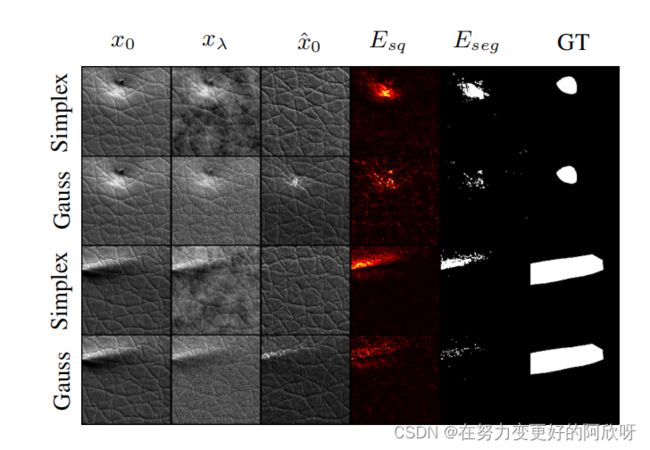
 在健康数据上，λ = 250对单纯形噪声（第1-2行）和高斯噪声（第3-4行）的前向向后扩散过程。   与单纯形噪声（第5行）不同，高斯扩散不能修复（第6行）不健康的异常测试数据。

二、Denoising Diffusion Probabilistic Models

  DDPMs在样本质量和模式覆盖方面已经成为生成建模的最新方法，DDPMs包括一个正向扩散过程q(xt|xt−1) 逐渐将某些目标分布q(x0)破坏为正态分布，以及一个学习过的反向过程pθ(xt−1|xt)，通过将噪声转化为q(x0)的样本来生成样本。

   正向过程是一个非齐次马尔可夫链，这意味着该过程的动力学可以用一步跃迁密度来描述。

对于t=1，...T。每一步添加的噪声量由方差计划βt ∈ (0, 1), t = 1, . . . , T.这可以定义为一个小的线性时间表，并由Ho等人更新，从β1 = 10−4线性增加到βT = 0.02。另外一种选择是Dhariwal and Nichol找到了一个余弦时间表也表现的很好。生成模型，参数化的θ，是从xT ∼ N (0, I)开始的学习反向过程，并根据

 对于t=T，.....，1，和β˜t，例如，µθ可以使用类似于U-Net的架构来实现。

 然后，训练pθ的损失函数pθ(xt−1|xt)可以被取为边界似然pθ(x0) 的变分下界Lvlb。

其中DKL表示Kullback-Leibler散度。上述损失确实是易于处理的，因为q(xt−1 | xt, x0) 有一个封闭形式的表达式。

在这项工作中，我们将考虑Ho等人的修改：αt = 1 − βt和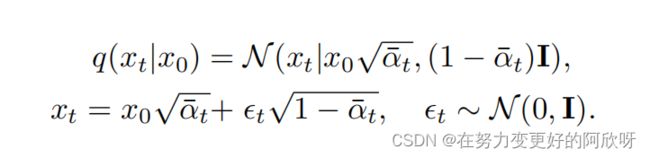

这允许对任意t快速采样xt，而不需要找到中间步骤xt−1, . . . , x1。

设置

 例如，我们可以像以前一样使用神经网络来学习ϵθ。事实证明，Ho等人发现以下简化目标结果的样品质量优于Lvlb。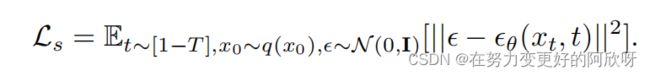

更简洁的说，Ls参考了Ho等人的Lsmipild

三、方法

自然图像已被证明具有频率的幂律分布，其中较低频率分量对图像的贡献更大。由于高斯白噪声具有均匀的光谱密度，部分扩散图像的低频分量不会达到与高频项的破坏程度。这在图1中很明显，其中部分高斯扩散留下了一个很容易识别的初始图像视图。这限制了AnoDDPM模型的区分能力，因为低频分量被推断为相对无腐败的，导致在反向过程中重建了较大的异常区域。在异常和非异常图像都遵循幂律的假设下，我们动机修改扩散过程，使应用的噪声遵循相似的幂律，强烈影响低频分量。我们希望从一个遵循幂律的分布中进行抽样。虽然这些可以通过二维高斯随机场或过程来计算，或者通过仔细构造一个协方差矩阵，但我们可以用单纯形噪声来近似它。单纯形噪声使我们能够精确地控制图像中频率的分布。与经典的白噪声相比，单纯形噪声和相关概念产生平滑或结构化的随机性，使它们在计算机图形中流行起来，例如，对于自动生成的结构，如景观。

3.1Simplex Noise

对于二维情况，例如，Perlin噪声的产生如下：首先，在一个晶格上采样随机梯度，然后，对于任何候选点，我们计算梯度与候选点距最近的4个格点的偏移之间的内积。所得到的值随后被插值，产生平滑的噪声。更先进的单纯形噪声用等边三角形的单纯形格取代了格。这降低了维度的复杂性，并减少了基于Perlin噪声的定向人工干扰。图2是一个单纯形噪声的例子，结构差异在视觉上是直接的，而这种噪声相对于标准高斯扰动的潜在好处是直观的：腐败更具结构化，去噪过程将能够“修复”这些结构化的异常。

 3.2.AnoDDPM

我们的异常检测分割方法探索了使用具有高斯噪声或单纯形噪声的ddpm。最初，查询图像x0为t时间步xt损坏，然后去噪回xˆ0。由于异常的大小可能不同，我们将xt参数化到xλ，其中较大的λ值可以消除较大的异常。

我们不使用默认的单纯形噪声函数，而可以应用一些八度噪声，也称为分形噪声）。这涉及到将N个噪声频率组合在一起，其中下一个频率的振幅降低了一些衰减率γ。图2b显示，低频噪声不能很好地近似为高斯分布；然而，通过增加八度数的噪声，该分布变得更接近高斯分布。这对于我们的DDPM模型来说是最重要的，因为我们假设我们的噪声函数是从高斯分布中采样的。因此，除非另有说明，我们使用ν=2−6的起始频率，N = 6的八度值和γ = 0.8的衰减。此外，当产生单纯形噪声时，我们在每次噪声计算前打乱种子，并从三维噪声函数中取一个切片t，因为我们发现在从二维噪声函数中采样时引入了伪影。

3.3Traning

我们使用以下训练程序只在健康样本上训练我们的模型：

 3.4inference

在推理时，我们从我们的异常数据集a中获取一个查询，然后将其噪声到某个时间步长x0→xλ，然后将其去噪回xλ→x0.这可以看作是输入查询上的一个条件DDPM模型（见图1）。除非另有说明，我们使用λ = 250进行实验。因此，推理时间效率为O(λ)。经过这个重建，我们发现平方误差为重建和初始图像(x0 − xˆ0) 2，这是本文的热图。然后，为了分割肿瘤，我们取一个直率的阈值，这样任何大于0.5的误差都将被突出显示。为了进行评估，我们可以将预测与地面真相进行比较。

 3.5. 实现和可用性

对于我们所有的DDPM，我们使用与Dhariwal和Nichol相同的UNet 架构作为我们的ϵθ近似。这是基于PixelCNN [19]和Wide ResNet [28]，使用变压器正弦位置嵌入[26]来编码时间步长。模型超参数包括：

该模型用PyTorch实现，并在一个具有12GB GDDR5的NVIDIA泰坦Xp GPU上进行训练。该代码在麻省理工学院许可下发布，并可在：（Github URL https://github.com/JulianWyatt/AnoDDPM）获得。

3.6. Datasets

对于我们的健康数据集，我们使用了神经反馈颅骨剥离（NFBS）存储库，其中包含125张t1加权MRI扫描，尺寸为256×256×192，包括完整的头骨，被剥离的头骨和大脑面具。我们使用完整的颅骨图像作为异常可以出现在任何地方，尽管这增加了问题的复杂性。我们使用2D256×192的大脑轴向切片，因为异常通常更容易从这个角度中被发现。然后，我们通过随机选择一个整数i∈[40,100]来选择切片。对于预处理，我们应用了±3◦的随机旋转和0.02×宽度和0.09×高度的随机平移。 然后中心裁剪235，其大小调整为256*256。 这分为100个培训卷和25个测试卷。

为了进行评估，我们使用了一个脑肿瘤的异常数据集，除非另有说明.该数据集包含了由爱丁堡大学临床脑科学中心提供的22张t1加权MRI扫描图。该数据集包括256×256×156的非颅骨剥离扫描。该数据集包含图像强度的不均匀性，这是磁场变化的结果，而不是解剖差异。因此，我们对图像应用了脑套件偏置场校正。对于我们的分析，我们将轴向扫描集中裁剪到175×240，然后调整大小到256×256，以保持训练集的长宽比。

4. Experiments and Results

为了进行我们的评估，我们试图分割数据集中所有22张图像的异常，其中我们使用了4个包含肿瘤的等距切片。我们可以用高斯噪声或单纯形噪声进行条件重构，因此，我们评估了噪声函数对异常检测的影响。此外，我们在MVTec AD数据集的皮革子集上对具有单纯形和高斯噪声的AnoDDPM进行采样，其结果是良好的重建，如图所示。因此，它可以很好地在替代领域工作。我们通过将图像转换为灰度来对数据集进行预处理，并从原始的1024×1024图像中生成一个256×256的随机裁剪。

4.1. Gaussian vs. simplex noise

如图3（底部）所示，很明显，高斯噪声产生了更高质量的样本，然而，在将图像腐蚀为更大的t后，图像的细节被丢失和改变，在λ = 750产生了一个完全不同的样本。相反，图3（顶部和中间）中的单纯形噪声捕获了噪声频率对异常检测的影响。结果表明，随着多尺度噪声的最大频率的增加，更多的肿瘤被破坏，然后重建为一个健康的近似。

我们还评估了产生最佳分割的释放时间t，如图

 

 这两个大的肿瘤导致了一个非常不同的最佳释放时间t，这表明最佳t不仅仅取决于异常区域的大小。因此，执行网格搜索，我们根据经验发现，λ = 250对于这个特定的数据集是最优的。

最后，我们计算了接收机工作特征曲线（ROC曲线），图6，它比较了上下文编码器重构方法、f-AnoGAN 、具有高斯噪声的AnoDDPM和具有单纯形噪声的AnoDDPM。我们使用平方误差概率（x−xˆ）2来寻找真阳性率和假阳性率。如图6所示，高斯噪声的AnoDDPM在我们的异常数据集[16]上的表现略优于随机，而单纯噪声的AnoDDPM表现很好，一般优于f-AnoGAN[20]（在64x64切片上训练）。

 4.2. Discussion

我们观察到单纯形模型的样本质量略有下降，特别是当噪声增加到进一步的t值时。这可能是由于单纯形噪声函数的不对称性；在未来的工作中，可以通过探索更广泛的噪声函数或设计自定义的多频噪声函数来探索这方面的替代选择。此外，由于该算法表现为随机的，未来的工作可以探索多次采样xλ，并对相应的重构xˆ0进行平均。

 此外，该模型难以分割位于其他高频信息附近的肿瘤，如脑回和脑沟周围。 这里可以进行进一步的工作，通过使用修复方法以不同的量对图像的不同部分进行噪声处理来改善这一点。我们还经历了一些样本，它们将大脑的特征，如侧脑室，引入到不应该包含这些特征的切片中。因此，通过更大的训练和测试语料库，可以评估和探索一个以切片为条件的引导扩散模型.

在未来，我们想看看带有单纯形噪声的AnoDDPM方法是否可以利用三维图像或彩色图像中的额外信息，并扩展到其他异常检测图像数据集和应用程序，像X射线行李安全、生物图像和假冒产品。

5. Conclusion

总之，我们发现具有单纯形噪声的AnoDDPM通过不需要大数据集的稳定训练成功捕获了大的异常区域，避免了基于GAN的方法中常见的局限性。在医疗和非医疗应用中，使用多标量（单纯形）噪声代替高斯噪声在捕获更大的异常形状方面提供了显著的改进。在未来，这将有利于进一步研究不同的噪声类型如何对应于使用AnoDDPM方法的其他异常检测应用程序，如在自动威胁检测和假冒产品检测中。特别是，在T1加权脑MRI异常检测应用中，发现具有单纯形噪声的AnoDDPM在分割（DICE、IoU）和分类度量（AUC）方面优于其高斯噪声对应物以及f-AnoGAN。所提出的部分扩散策略确保了该方法在高分辨率图像中保持性能（整个纸张的图像最好被放大）。我们希望这种方法也能在其他不需要全长马尔可夫链的应用中取得成功，如在图像增强、语义分割和过滤方面。

6.合规性

本研究中使用的培训数据是由内森·克莱恩研究所收集并匿名提供的，该研究所支持大规模开放获取的健康数据 。这些数据是根据健康保险可携性和责任法案（HIPAA）获得的。评估数据是匿名的，并由爱丁堡大学临床脑科学中心开放获取。患者被给予一个可识别的随机代码，数据收集者保存了一个记录。