Games101-课程15笔记

目录

总结上节课的公式

Irradiance(辐照度)

定义

Radiance(辐射度)

定义

公式解析

irradiance / intensity 和 radiance的区别

Incident Radiance(入射辐射度)

定义

Exiting Radiance(出射辐射度)

定义

辐射度vs辐照度

双向反射率分布函数(BRDF)

概述

如何知道收集到的Radiance, 反射到哪个方向?

BRDF的定义

反射方程

困难：递归方程

通用渲染方程

① 重写反射方程

② 得到更通用渲染方程

分析渲染方程如何得出

① 假设只有一个点光源

② 假设有好多点光源

③ 假设有一个面光源和多个点光源

④ 假设除了以上的入射光, 还有其它的物体反射来的入射光

将渲染方程作为积分方程

 线性算子方程

 光线追踪和扩展

 该公式的相关参数解析

光照的实际应用

总结: 亮度会收敛到某种程度, 因为能量守恒

概率论

 性质: 概率必须大于0, 所有概率相加为1

 随机变量的期望值

期望值

均值 

连续函数案例：概率分布函数

随机变量的函数

---

第十五节课 :光线追踪(Ray Tracing 3)

总结上节课的公式:

Irradiance(辐照度): 落在表面上的光

-对应面积上所有的能量

定义: 单位时间内投射到单位面积上的辐射能量

光若不垂直投影曲面, 有夹角(斜着), 接收到的能量会减小.

物体表面上的辐照度与(光方向和表面法线)之间的夹角一致成正比.

就好比下图的Lambert’s Cosine Law, 所接受的能量与cos(光方向和表面法线)相关.

我们为什么有季节(春夏秋冬)?

就是因为太阳光线不是一直垂直照射地球某个地方.

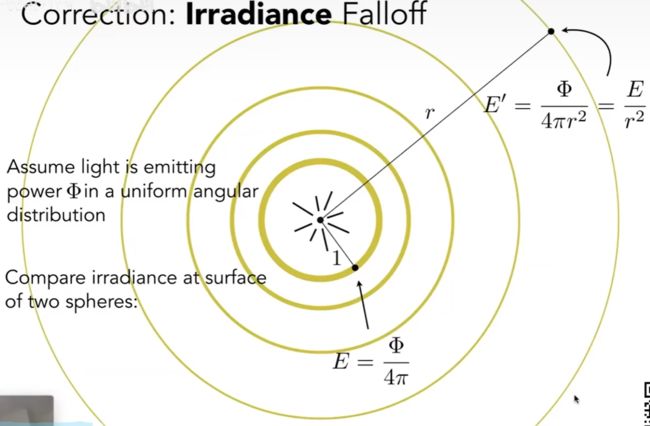
假设光以均匀的角分布发射功率

比较两个球体表面的辐照度, 发现辐照度会因为半径的增加而衰弱;

再比较两个球体表面的辐射强度

根据公式发现, 它不会因为半径(距离)的增加而衰弱, 而是不变, 影响它的只有单位能量和单位立体角, 近距离和远距离立体角都不变.

Radiance(辐射度)

定义 :

① 描述光在环境中传播的基本属性

② 与光线相关联的量

③ 渲染是与计算radiance(辐射度)有关

--(光沿着光线传播)

对于Radiance(辐射度)的理解:     从一个面积往立体角方向辐射出能量

公式解析:

① 下图中的面可能会往各个方向都辐射能量, 这里只研究它其中一个微分(单位)方向.

② 下图中的面需要确认面积, 这与它受到的能量大小有关, 这里只研究它一个微分(单位)面积

所以公式为: 两个微分的相乘

这两个微分解释分别为: (① 每单位立体角、② 每投影单位面积的表面发射、反射、传输或接收的辐射功率)

①②相乘, 得出 ( d辐射功率/d投影面积/d立体角 ), ps:请记住下面有用

定义如下:

① 辐照度(irradiance)：每单位投影面积的辐射功率( d辐射功率/d投影面积 )

② 辐射强度(Intensity)：每单位立体角的辐射功率( d辐射功率/d立体角 )

根据intensity,irradiance和 radiance(①*②)的定义得出:

① 辐射度(Radiance)：每单位立体角的辐照度( 辐照度/d立体角 )

② 辐射度(Radiance)：每单位投影面积的辐射强度( 辐射强度/d投影面积 )

所以得出, irradiance/intensity和 radiance的区别是:

前者不考虑方向(投影面积的能量), 后者考虑方向(只考虑一个方向进入投影面积的能量), 方向性的区别.

Incident Radiance(入射辐射度)

定义: 入射辐射度是到达表面的每单位立体角的辐照度。

-即它是沿着给定光线到达表面的光（表面上的点和入射方向）

Exiting Radiance(出射辐射度)

定义: 出射表面的辐射度是离开表面的每单位投影面积的强度

例如，对于区域光，它是沿给定光线发射的光（表面上的点和出射方向）

辐射度vs辐照度

辐射度(Radiance)：面积 dA 从“方向”dw 接收的功率

辐照度(Irradiance)：面积 dA 接收的总功率

是半球的体积: (2/3)πr3

双向反射率分布函数(BRDF)

概述: 来自方向 wi 的入射辐射度变成了点面积 dA 接收到的功率 E , 那么功率 E 将变成到其他方向 wr 的出射辐射度

如何知道收集到的Radiance, 反射到哪个方向?

答: 使用BRDF

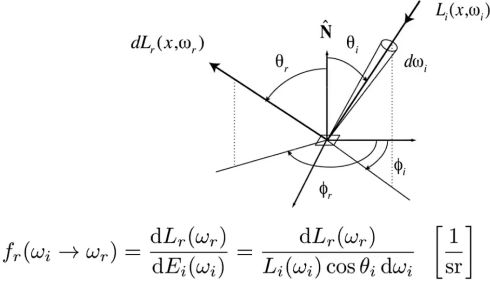
BRDF的定义:

① 表示有多少光从每个入射方向反射到每个出射方向 wr

② 类似于接受到的能量所反射的能量分布

③ 比如用于定义材质(漫反射材质, 抛光/毛面金属材质, 完全镜面反射+折射材质等等)

④ 公式意思: Radiance(辐射度)/irradiance(辐照度)

反射方程:

相关变量:

wr : 观测方向                wi : 入射方向                dwi : 每一个入射方向

:  Irradiance的表达式                : 上面求出的BRDF

: 单元半球,   表示单元半球内全部对出射方向的Lr(x,wr)作贡献的都相加

Irradiance( 着色面积所受能量 )* BRDF = 观测方向的出射辐射度.

困难：递归方程

反射辐照度取决于入射辐射度

但是入射辐射度不止有来自点光源的, 还有经过别的物体（在场景中的另一点）反射而来的反射辐射度

通用渲染方程

① 重写反射方程：

如果本身会发光, 通过添加自身辐射度使其通用:

注意：现在，我们假设所有方向都指向外面(比如wi是入射,但是还是写作方向从球心向外)

等于, 都是表示只考虑半球内的光线, 如果从底下入射, 无意义所以不考虑.

 等于

② 得到更通用渲染方程, 如下:

分析渲染方程如何得出:

① 假设只有一个点光源, 得出的反射方程:

反射光(输出图片)= 自身光+入射光(点光源)*BRDF*入射角的余弦

② 假设有好多点光源, 得出的反射方程:

反射光(输出图片)= 自身光+对所有光源求和[入射光(点光源)*BRDF*入射角的余弦]

 

③ 假设有一个面光源和多个点光源, 得出的反射方程:

用积分替换总和, 其余和处理多个点光源一样.

 

④ 假设除了以上的入射光, 还有其它的物体反射来的入射光, 得出的反射公式:

反射光(观测方向)未知, 其它物体反射来的入射光未知. 其它都已知, 只需要把(其它物体反射来的入射光)当作(点光源)处理.

 

将渲染方程作为积分方程

变量详解:

u表示观测方向, 等于wr                v表示入射方向, 等于wi                x表示功率

 等于  , 表示观测方向(摄像头)接受到的光.

等于  , 表示着色点自身的发光

等于  , 表示入射光

(核心) ==  ,表示把全部的入射光转换到观测方向的光

是第二类 [广泛研究数值] 的 fredholm 积分方程，其典型来自

 

 线性算子方程(算是一种简化, 中间过程复杂)

表示光传输算子方程的核

可以离散为一个简单的矩阵方程[或联立线性方程组]

L,E 是向量，L是最后看到的能量, E是自身具有的能量

K 是光传输矩阵(反射操作符)

 

光线追踪和扩展(解出L)

1.一般类数值蒙特卡罗方法

2.场景中所有光路的近似集合

I表示单位矩阵, 通过一系列的数学运算得出L

为什么要用算子?

因为要得到这个形式的公式 

该公式的相关参数解析

K是反射运算符

E : 直接从光源发射 (在着色点发光)

KE : 表面直接光照 (直接射向着色点,反射到达观测点)

 : 间接光照（一次间接反弹）[镜子，折射]

... : 表示还有间接更多次的反射

 光栅化一般只有E (自发光) 和 KE (直接光照) , 也有可能有K2E,K3E(少数)

 光照的实际应用

 直接光照

(光照只反射了一次到摄像机, 点光源打到哪里, 哪里就有颜色, 不然就是黑色)

ps: 第一次反射就看到上方的灯, 因为光没有进去灯里.

 全局光照

(考虑光照反射一次和两次)

 全局光照

(考虑光照反射一次,两次和三次)

全局光照(考虑光照反射一次,两次,三次,四次和五次)

可以发现下图中上方的灯与上图中对比, 明显亮了.

这是因为这个灯是双层的玻璃, 光线进入需要两次反射, 出来也需要两次反射. 所以在上图的最多反射三次的情况下, 看不见玻璃灯.

 全局光照(考虑光照反射一次,两次,三次,直到八次)

现象: 发现在全局光照(最多四次~八次甚至到十六次)时, 变亮的效果越来越低, 直到亮度不再变化(肉眼上)

总结: 亮度会收敛到某种程度. 因为能量守恒.

概率论(probability review)

随机变量: 表示潜在值的分布 

概率密度函数 (PDF): 描述随机过程选择值 x 的相对概率

示例：连续PDF函数：域上的所有值均等可能

例如 六个面的骰子,  X 取值 1,2,3,4,5,6, 摇得任意一个面的概率一致为: 1/6

 性质: 概率必须大于0, 所有概率相加为1.

随机变量的期望值

定义 :从随机分布中重复抽取样本所获得的平均值

X 的期望值:  

均值 ：

连续函数案例：概率分布函数

一个随机变量 X，可以取任意一组连续值，其中特定值的相对概率由连续概率密度函数 p(x) 给出, 一段连续的x值形成的面积就是概率.

p(x) 的条件: , 和(概率>0且全部概率相加=1) 一个意思

期待值: 

随机变量的函数

① 随机变量X的函数Y,也是随机变量

② 随机变量函数的期望值