Python解决经典八皇后问题（附可视化代码，直接运行即可！）

Python解决经典八皇后问题

问题描述：

在8*8的棋盘上，放置八个皇后。
要求8个皇后都不在同一行，同一列，同一斜线上

如图是其中一种解：

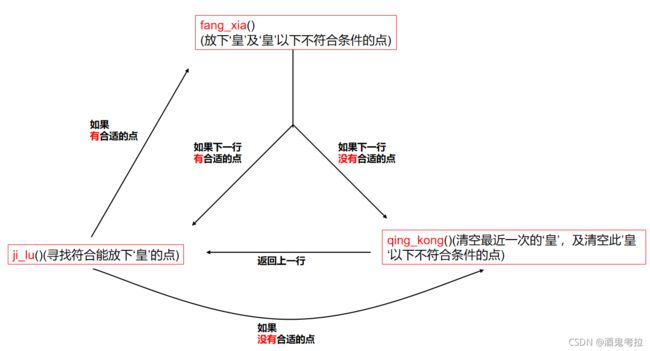
解决此问题大致思路如下图：(从ji_lu()函数开始)

用递归可以找出所有解，并记录，可视化代码如下，直接运行即可：(附上各个步骤详解的ppt)

1.输出所有解：

l1=[[[] for i in range(8)]for i in range(8)]#l1设为8*8的二维列表，每一个元素为'[]'表示空
l2=[[0 for i in range(8)]for i in range(8)]#l2设为8*8的二维列表，每一个元素为0,此列表用于输出优化
number=0#number为记录满足条件解的数量

#ji_lu函数用于记录l1列表中每行元素为'[]'的位置(二维列表的下标)
#设置shu_zi参数目的为了不与其他行的条件产生冲突(数字0-7分别代表0-7行)
#m代表行(初始0行)
def ji_lu(m,shu_zi):
    for n in range(8):#n代表列每次调用ji_lu函数都会遍历本行的所有列
        if l1[m][n]==[]:
            fang_xia(m,n)
            qing_kong(m,n,shu_zi)

#qing_kong函数用于遍历l1列表中所有的元素并清空不满足fang_xia函数中的元素(相当于返回上一步)
def qing_kong(p,q,shu_zi1):
    l1[p][q]=[]
    for a in range(8):
        for b in range(8):
            if l1[a][b]==shu_zi1:
                l1[a][b]=[]
                
#fang_xia函数用于放下符合条件的皇后('皇'),
#然后判断本行以下的所有行中满足条件为'[]'的元素
#并跳转到下一行用于ji_lu函数判断
def fang_xia(i,j):
    global number
    shu_zi2=i#将i(行位置)赋予shu_zi2 目的不跟别的行判断的条件冲突
    l1[i][j]='皇'#将传入此函数的列表的位置,改为'皇'
    for ix in range(i+1,8):#此位置的列固定,将此列以下所有行中的元素改为shu_zi2
        if l1[ix][j]==[]:
            l1[ix][j]=shu_zi2
    a1=i
    b1=j
    for p in range(7-j if 7-j<7-i else 7-i):#此位置固定,将此位置右下斜线中的所有元素改为shu_zi2
        a1=a1+1
        b1=b1+1
        if l1[a1][b1]==[]:
            l1[a1][b1]=shu_zi2
    a2=i
    b2=j
    for u in range(j if 7-i>j else 7-i):#此位置固定,将此位置左下斜线中的所有元素改为shu_zi2
        a2=a2+1
        b2=b2-1
        if l1[a2][b2]==[]:
            l1[a2][b2]=shu_zi2
    if i+1!=8:
        shu_zi2=shu_zi2+1
        ji_lu(i+1,shu_zi2)
    if i==7:#如果每行都遍历完成，则输出解
        for i in range(8):
            for j in range(8):
                if l1[i][j]=='皇':
                    l2[i][j]=l1[i][j]
        number=number+1
        print('第'+str(number)+'种解为:')
        for i in range(8):
            for j in range(8):
                print(l2[i][j],end='\t')
                l2[i][j]=0
            print('\n')
        print('\n')
ji_lu(0,0)
print('8皇后问题共有'+ str(number)+'种解')

2.输单个解：

l1=[[[] for i in range(8)]for i in range(8)]#l1设为8*8的二维列表，每一个元素为'[]'表示空
l2=[[0 for i in range(8)]for i in range(8)]#l2设为8*8的二维列表，每一个元素为0,此列表用于记录每一种解
l3=[]#l3设为输出优化，用于传递用户想查看的1到92种解
count=0#number为记录满足条件解的数量
def ji_lu(hang,number):
    ''' ji_lu函数用于记录l1列表中每行元素为'[]'的位置(二维列表的下标)
    设置number参数目的为了不与其他行的条件产生冲突(数字0-7分别代表0-7行)
    m代表行(初始0行)
    '''
    global nums
    for lie in range(8):#n代表列每次调用ji_lu函数都会遍历本行的所有列
        if l1[hang][lie]==[]:
            fang_xia(hang,lie)
            qing_kong(hang,lie,number)

def qing_kong(hang,lie,number):
    ''' qing_kong函数用于遍历l1列表中所有的元素
    并清空不满足fang_xia函数中的元素(相当于返回
    上一步)
    '''
    l1[hang][lie]=[]
    for a in range(8):
        for b in range(8):
            if l1[a][b]==number:
                l1[a][b]=[]
                
def fang_xia(hang,lie):
    ''' fang_xia函数用于放下符合条件的皇后('皇'),
    然后判断本行以下的所有行中满足条件为'[]'的元素
    并跳转到下一行用于ji_lu函数判断
    '''
    global count#全局变量，用于记录解的数量
    
    number=hang#将i(行位置)赋予number 目的不跟别的行判断的条件冲突
    l1[hang][lie]='皇'#将传入此函数的列表的位置,改为'皇'
    for i in range(hang+1,8):#此位置的列固定,将此列以下所有行中的元素改number
        if l1[i][lie]==[]:
            l1[i][lie]=number
    a1,b1=hang,lie#a1,a2,b1,b2用于传递行(hang)以及列(hang)并执行自加操作
    for p in range(7-lie if 7-lie<7-hang else 7-hang):#此位置固定,将此位置右下斜线中的所有元素改为number
        a1=a1+1
        b1=b1+1
        if l1[a1][b1]==[]:
            l1[a1][b1]=number
    a2,b2=hang,lie
    for u in range(lie if 7-hang>lie else 7-hang):#此位置固定,将此位置左下斜线中的所有元素改为number
        a2=a2+1
        b2=b2-1
        if l1[a2][b2]==[]:
            l1[a2][b2]=number
    if hang!=7:
        ji_lu(hang+1,number+1)#若行数没有遍历完成，并且还有情况能放下'皇'，
                              #则传递下一行(hang+1)和当前数字到ji_lu()函数中进行再判断
        
    if hang==7:#如果每行都遍历完成，则输出解
        for i in range(8):
            for j in range(8):
                if l1[i][j]=='皇':
                    l2[i][j]=l1[i][j]
        count=count+1
        for i in range(8):
            for j in range(8):
                l3.append(l2[i][j])
                l2[i][j]=0
ji_lu(0,0)

print('8皇后问题共有'+ str(count)+'种解')
n=int(input('''请输入要查看的第n(1-92)种解:\nn='''))
print('您选择的是查看第'+str(n)+'种解:')
for i in range(64):
    print(l3[i+(n-1)*64],end='\t')
    if (i+1)%8==0:
        print('\n\n')

步骤详解ppt
运行成功的记得回来点个赞哦！