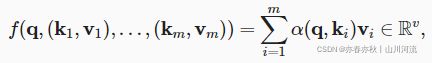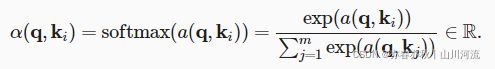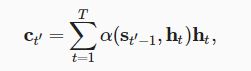注意力机制（Attention Mechanism）

注意力机制

• 卷积、全连接、池化层都只考虑不随意线索

• 注意力机制则显示的考虑随意线索

  • 随意线索被称之为查询（query）
  • 每个输入是一个值（value）和不随意线索（key）的对
  • 通过注意力池化层来有偏向性的选择某些输入

非参注意力池化层

• 给定数据（，），

• 平均池化是最简单的方案：

• 更好的方案是60年代提出来的Nadaraya-Watson核回归

Nadaraya-Watson核回归

使用高斯核

那么

总结

• 心理学任务人通过随意线索和不随意线索选择注意点
• 注意力机制中，通过query（随意线索）和key（不随意线索）来有偏向性的选择输入
  • 可以一般的写作 ,这里的是注意力权重
  • 早在60年代就有非参数的注意力机制
• 接下来会有多个不同的权重设计

  import torch
  from d2l import torch as d2l
  """为了可视化权重，定义show_heatmaps函数，输入matrices的形状是（要显示行数，要显示的列数，查询的数目，键的数目）"""
  def show_heatmaps(matrices, xlabel, ylabel, titles=None, figsize=(2.5,2.5), cmap='red')
      """显示矩阵热图"""
      d2l.use_svg_display()
      num_rows, num_cols = matrices.shape[0], matrices.shape[1]
      fig, axes = d2l.plt.subplots(num_rows, num_cols, figsize = figsize,             
                                   sharex=True,sharey=True, squeeze=False)
      for i , (row_axes, row_matrices) in enumerate(zip(axes,matrices)):
          for j, (ax, matrix)in enumerate(zip(row_axes, row_matrices)):
              pcm = ax.imshow(matrix.detach().numpy(), cmap = cmap)
              if i == num_rows - 1:
                  ax.set_xlabel(xlabel)
              if j == 0:
                  ax.set_ylabel(ylabel)
              if titles:
                  ax.set_title(titles[j])
      fig.colorbar(pcm, ax=axes, shrink=0.6);

注意力机制与全连接层或者池化层的区别在于增加了自主提示

注意力机制通过注意力池化使选择偏向于值（感官输入），其中包含查询（自主性提示）和键（非自主性提示）。键和值是成对的。 

注意力汇聚：Nadaraya-Watson核回归

查询（自主提示）和键（非自主提示）之间的交互形成了注意力池化，注意力池化有选择地聚合了值（感官输入）以生成最终的输出。

 回归问题：给定的成对的“输入——输出”数据集，如何学习f来预测任意新输入的x的输出?

n_train = 50  # 训练样本数
x_train, _ = torch.sort(torch.rand(n_train) * 5)   # 排序后的训练样本

def f(x):
    return 2 * torch.sin(x) + x**0.8

y_train = f(x_train) + torch.normal(0.0, 0.5, (n_train,))  # 训练样本的输出
x_test = torch.arange(0, 5, 0.1)  # 测试样本
y_truth = f(x_test)  # 测试样本的真实输出
n_test = len(x_test)  # 测试样本数
n_test

def plot_kernel_reg(y_hat):
    d2l.plot(x_test, [y_truth, y_hat], 'x', 'y', legend=['Truth', 'Pred'],
             xlim=[0, 5], ylim=[-1, 5])
    d2l.plt.plot(x_train, y_train, 'o', alpha=0.5);

基于平均池化来计算所有训练样本输出值的平均值

y_hat = torch.repeat_interleave(y_train.mean(), n_test)
plot_kernel_reg(y_hat)

非参数注意力池化

平均池化忽略了输入

根据输入的位置对输出进行加权

 K是核（kernel）

注意力池化公式

 是查询，是键值对，注意力池化是的加权平均。x和xi之间的关系建模为注意力权重（attention weigh），此权重被分配给每一个对应值yi。

对于任何查询，模型在所有键值对注意力权重都是一个有效的概率分布；是非负的，并且总和为1.

考虑高斯核（Gaussian kernel）

   代入得到

 即如果一个xi越是接近给定的查询x，那么分配给这个键对应值yi的注意力权重就会越大，也就获得了更多的注意力

非参数的注意力池化（Nonparametric attention pooling）模型

带参数的注意力池化

查询x和键xi之间的距离乘以可学习参数 

---

注意力评分函数

高斯核指数部分视为注意力评分函数（attention scoring function），将此函数的输出结果输入到softmax函数中进行运输。得到与键对应的值的概率分布（注意力权重）。注意力池化的输出就是基于这些注意力权重的值的加权和。

计算注意力池化的输出为值的加权和 

假设有一个查询和m个“键-值”对，其中，

注意力池化函数f就被表示成值的加权和：

查询q和键的注意力权重（标量）是通过注意力评分函数α将两个向量映射成标量，再经过softmax运算得到的：

选择不同的注意力评分函数α会导致不同的注意力池化操作。

掩蔽softmax操作(masked softmax operation)：任何超出有效长度的位置都被掩蔽并置为0

加性注意力（additive attention）

当查询和键是不同长度的矢量时，可使用。

 可学习的参数、、

将查询和键连结起来后输入到一个多层感知机（MLP）中，感知机包含一个隐藏层，其隐藏单元数是一个超参数h。使用tanh作为激活函数，并且禁用偏置项。

等价于将key和query合并起来后放入到一个大小为h，输出大小为1的单隐藏层MLP

如果query和key都是同样长度，那么可以

缩放点积注意力

使用点积可以得到计算效率较高的评分函数，但点积操作要求查询和键具有相同的长度d。

假设查询和键的所有元素都是独立的随机变量，并且都满足零均值和单位方差，那么两个向量的点积的均值为0，方差为d。为确保无论向量长度如何，点积的方差在不考虑向量长度的情况下仍然是1，我们将点积除以。

 

小结

将注意力池化的输出计算可以作为值的加权平均，选择不同的注意力评分函数会带来不同的注意力汇聚操作。

当查询和键是不同长度的矢量时，可以使用可加性注意力评分函数。当它们的长度相同时，使用缩放的“点——积”注意力评分函数的计算效率更高。

向量化版本

• 注意力分数是query和key的相似度，注意力权重是分数的softmax结果
• 两种常见的分数计算：
  • 将query和key合并起来进入一个单输出的单隐藏层的MLP
  • 直接将query和key做value

例如：k作为员工，v是员工薪水，q是自己，通过注意力得出自己的薪水

 

———————————————————————————————————————————

Bahdanau注意力（seq2seq）

模型

         没有严格单项对齐限制的可微注意力模型。在预测词元时，如果不是所有输入词元都相关，模型将仅对齐（或参）输入序列中与当前预测相关的部分。这是通过将上下文变量视为注意力集中的输出来实现的。

        假设输入序列中有T个词元，解码时间步t’的上下文变量是注意力集中的输出：

时间步t’-1时的解码器隐状态是查询，编辑器隐状态既是键，也是值，注意力权重α使用加性注意力评分函数。

定义注意力解码器

初始化解码器状态：

1. 编码器在所有时间步的最终层隐状态，将作为注意力的键和值；

2. 上一时间步的编码器全层隐状态，将作为初始化解码器的隐状态；

3. 编码器的有效长度（排除在注意力池中填充词元）

在每个解码时间步骤中，解码器上一个时间步的最终层隐状态将用作查询。因此注意力输出和输入嵌入都连结为循环神经网络解码器的输入。

class Seq2SeqAttentionDecoder(AttentionDecoder):
    def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
                 dropout=0, **kwargs):
        super(Seq2SeqAttentionDecoder, self).__init__(**kwargs)
        self.attention = d2l.AdditiveAttention(
            num_hiddens, num_hiddens, num_hiddens, dropout)
        self.embedding = nn.Embedding(vocab_size, embed_size)
        self.rnn = nn.GRU(
            embed_size + num_hiddens, num_hiddens, num_layers,
            dropout=dropout)
        self.dense = nn.Linear(num_hiddens, vocab_size)

    def init_state(self, enc_outputs, enc_valid_lens, *args):
        # outputs的形状为(batch_size，num_steps，num_hiddens).
        # hidden_state的形状为(num_layers，batch_size，num_hiddens)
        outputs, hidden_state = enc_outputs
        return (outputs.permute(1, 0, 2), hidden_state, enc_valid_lens)

    def forward(self, X, state):
        # enc_outputs的形状为(batch_size,num_steps,num_hiddens).
        # hidden_state的形状为(num_layers,batch_size,
        # num_hiddens)
        enc_outputs, hidden_state, enc_valid_lens = state
        # 输出X的形状为(num_steps,batch_size,embed_size)
        X = self.embedding(X).permute(1, 0, 2)
        outputs, self._attention_weights = [], []
        for x in X:
            # query的形状为(batch_size,1,num_hiddens)
            query = torch.unsqueeze(hidden_state[-1], dim=1)
            # context的形状为(batch_size,1,num_hiddens)
            context = self.attention(
                query, enc_outputs, enc_outputs, enc_valid_lens)
            # 在特征维度上连结
            x = torch.cat((context, torch.unsqueeze(x, dim=1)), dim=-1)
            # 将x变形为(1,batch_size,embed_size+num_hiddens)
            out, hidden_state = self.rnn(x.permute(1, 0, 2), hidden_state)
            outputs.append(out)
            self._attention_weights.append(self.attention.attention_weights)
        # 全连接层变换后，outputs的形状为
        # (num_steps,batch_size,vocab_size)
        outputs = self.dense(torch.cat(outputs, dim=0))
        return outputs.permute(1, 0, 2), [enc_outputs, hidden_state,
                                          enc_valid_lens]

    @property
    def attention_weights(self):
        return self._attention_weights

小结

在预测词元时，如果不是所有输入词元都是相关的，那么具有BAhdanau注意力的循环神经网络编码器-解码器会有选择地统计输入序列的不同部分。这是通过上下文变量视为加性注意力池化的输出来实现的

在循环神经网络编码器——解码器中，Bahdanau注意力将上一时间步的解码器隐状态视为查询，在所有时间步的编码器隐状态同时视为键和值。

---