Group conv vs. Depthwise separable conv
本王有话说:这俩属于是做轻量化绕不开的经典工作,盘踞武林好多年,我们的目标学会并企图超越它。
分组卷积(Group conv)
paper
原理
分组卷积,即ResNeXt的亮点,受Inception和AlexNet的启发产生。Inception中提到,对于卷积来说,卷积核可以看做一个三维滤波器:通道维+空间维(特指特征图的W和H),常规的卷积操作其实就是实现通道相关性和空间相关性的联合映射。Inception提出假设: 卷积层通道间的相关性和空间相关性是可以退耦合的,将它们分开映射,能达到更好的效果。具体来说,不同卷积操作得到的特征图之间的耦合性较低,关注的主要特征不同,得到的特征图互为补充能够表示更完整的图像。
如下图(b)所示,分组卷积将得到g个互补的特征,然后将得到的特征进行concat组合,作为最终的输出特征图。

具体操作:如上图(b)所示,将(a)中常规卷积的输入分成g组,每个卷积核也相应地分成g组,在对应的组内分别做卷积,每组卷积都生成一个feature map,共生成g个feature map。
假设 input.shape = [c1, H, W] 、 output.shape = [c2, H, W]、 kernel_size=h1*w1
(a)常规卷积参数量=h1 * w1 * c1 * c2
(b)分组卷积参数量=h1 * w1 * (c1/g) * (c2/g) * g = h1 * w1 * c1 * c2 / g,其中g为分组数量。
效果
官方观点:group conv能够增加 filter之间的对角相关性,而且能够减少训练参数,避免过拟合,类似于正则化效果。
本王认为:换个角度,用少量的参数量和运算量就能生成大量的feature map,大量的feature map意味着能够编码更多的信息,所以分组卷积可以用同等运算量生成g倍的特征图,应该有更好的精度。
实现
import torch
import torch.nn as nn
...
model = nn.Conv2d(in_channels = in_channel, out_channels = out_channel, kernel_size = kernel_size, stride = stride, padding = 1, dilation = dilation, group = group_num)
ps: 分组数量(group_num)须能被输入通道数(in_channels)和输出通道数(out_channels)整除。
从分组卷积的角度来看,分组数就像一个控制旋钮,最小值是1,此时的分组卷积就是普通卷积;分组数最大值是输入feature map的通道数,此时的卷积就是深度分离卷积,又叫逐通道卷积。但后者有两次卷积操作,因为深度可分离卷积进行一次卷积无法达到输出指定维度的tensor,所以又用了1*1卷积改变最终输出的通道数。
深度可分离卷积(Depthwise separable conv)
paper
原理
深度可分离卷积,即MobileNet的精髓,由deep_wise卷积和point_wise卷积两部分组成,将卷积层通道相关性和空间相关性分开映射,达到更好的效果。
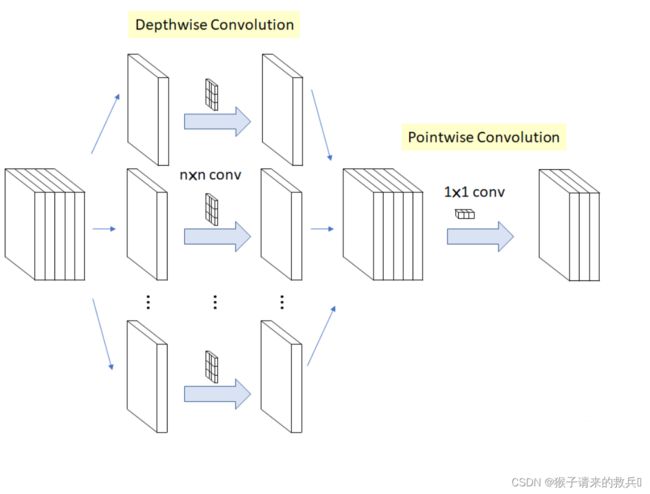
具体操作:进行了两次卷积操作。假设input.shape = [c1, H, W] 、output.shape = [c2, H, W]
- 第一次先进行deep_wise卷积(b)(即收集每一层的特征),kernel_size = n * n,第一次卷积的参数量为n * n * Cin ;
- 第二次是用point_wise卷积得到Cout维度的输出(b),kernel_size = 1 * 1,第二次卷积的参数量为1 * 1* Cin * Cout。
(a)常规卷积参数量=n * n * c1 * c2
(b)深度可分离卷积参数量=n * n * c1 + 1 * 1 * c1 * c2
效果
深度可分离卷积同时考虑了图像的空间和通道(首先考虑空间depth_wise,然后再考虑通道point_wise),实现了图像的空间和通道的完全分离。
本王有话说:深度可分离卷积是最高效的卷积形式,相比普通卷积,用同等的参数量和运算量就能够生成个feature map,而普通卷积只能生成一个feature map。所以深度分离卷积几乎是构造轻量高效模型的必用结构,如Xception, MobileNet, MobileNet V2, ShuffleNet, ShuffleNet V2, CondenseNet等轻量型网络结构中的必用结构。
实现
import torch
import torch.nn as nn
...
model = nn.Sequential(
nn.Conv2d(in_channels = in_channel, out_channels = in_channel, kernel_size = kernel_size, stride = stride, padding = 1, dilation = dilation, group = in_channel),
nn.Conv2d(in_channels = in_channel, out_channels = out_channel kernel_size = 1, padding = 0)
)
ps: 第一个conv处,group=in_channel=out_channel,所以参数量=(n * n * c1 * c1 ) /c1+ 1 * 1 * c1 * c2=n * n * c1 + c1 * c2
