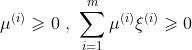- 机器学习与深度学习间关系与区别
ℒℴѵℯ心·动ꦿ໊ོ꫞
人工智能学习深度学习python
一、机器学习概述定义机器学习(MachineLearning,ML)是一种通过数据驱动的方法,利用统计学和计算算法来训练模型,使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本,识别其中的模式和规律,从而对新的数据进行判断。其核心在于通过训练过程,让模型不断优化和提升其预测准确性。主要类型1.监督学习(SupervisedLearning)监督学习是指在训练数据集中包含输入
- Goolge earth studio 进阶4——路径修改与平滑
陟彼高冈yu
Googleearthstudio进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径,所以当我们通过这个关键帧时,不是一个生硬的角度,而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄,允许我们调整路径的形状。右键单击,我们可以选择“平滑路径”,这是默认的自动平滑算法,或者我们可
- 基于社交网络算法优化的二维最大熵图像分割
智能算法研学社(Jack旭)
智能优化算法应用图像分割算法php开发语言
智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果:5.参考文献:6.Matlab代码摘要:本文介绍基于最大熵的图像分割,并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前,请阅读《图像分割:直方图区域划分及信息统计介绍》htt
- 121. 买卖股票的最佳时机
薄荷糖的味道_fb40
给定一个数组,它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天(股票价格=1)的时候买入,在第5天(股票价格=6)的时候卖出,最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
- 每日算法&面试题,大厂特训二十八天——第二十天(树)
肥学
⚡算法题⚡面试题每日精进java算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题,最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧!!特别介绍小白练手专栏,适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
- 回溯算法-重新安排行程
chirou_
算法数据结构图论c++图搜索
leetcode332.重新安排行程这题我还没自己ac过,只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多,用什么数据结构去存数据,去读取数据,都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
- Faiss:高效相似性搜索与聚类的利器
网络·魚
大数据faiss
Faiss是一个针对大规模向量集合的相似性搜索库,由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构,用于加速向量之间的相似性搜索,特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理:近似最近邻搜索:Faiss的核心功能之一是近似最近邻搜索,它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的,
- insert into select 主键自增_mybatis拦截器实现主键自动生成
weixin_39521651
insertintoselect主键自增mybatisdelete返回值mybatisinsert返回主键mybatisinsert返回对象mybatisplusinsert返回主键mybatisplus插入生成id
前言前阵子和朋友聊天,他说他们项目有个需求,要实现主键自动生成,不想每次新增的时候,都手动设置主键。于是我就问他,那你们数据库表设置主键自动递增不就得了。他的回答是他们项目目前的id都是采用雪花算法来生成,因此为了项目稳定性,不会切换id的生成方式。朋友问我有没有什么实现思路,他们公司的orm框架是mybatis,我就建议他说,不然让你老大把mybatis切换成mybatis-plus。mybat
- k均值聚类算法考试例题_k均值算法(k均值聚类算法计算题)
寻找你83497
k均值聚类算法考试例题
?算法:第一步:选K个初始聚类中心,z1(1),z2(1),…,zK(1),其中括号内的序号为寻找聚类中心的迭代运算的次序号。聚类中心的向量值可任意设定,例如可选开始的K个.k均值聚类:---------一种硬聚类算法,隶属度只有两个取值0或1,提出的基本根据是“类内误差平方和最小化”准则;模糊的c均值聚类算法:--------一种模糊聚类算法,是.K均值聚类算法是先随机选取K个对象作为初始的聚类
- Python实现简单的机器学习算法
master_chenchengg
pythonpython办公效率python开发IT
Python实现简单的机器学习算法开篇:初探机器学习的奇妙之旅搭建环境:一切从安装开始必备工具箱第一步:安装Anaconda和JupyterNotebook小贴士:如何配置Python环境变量算法初体验:从零开始的Python机器学习线性回归:让数据说话数据准备:从哪里找数据编码实战:Python实现线性回归模型评估:如何判断模型好坏逻辑回归:从分类开始理论入门:什么是逻辑回归代码实现:使用skl
- 推荐算法_隐语义-梯度下降
_feivirus_
算法机器学习和数学推荐算法机器学习隐语义
importnumpyasnp1.模型实现"""inputrate_matrix:M行N列的评分矩阵,值为P*Q.P:初始化用户特征矩阵M*K.Q:初始化物品特征矩阵K*N.latent_feature_cnt:隐特征的向量个数max_iteration:最大迭代次数alpha:步长lamda:正则化系数output分解之后的P和Q"""defLFM_grad_desc(rate_matrix,l
- K近邻算法_分类鸢尾花数据集
_feivirus_
算法机器学习和数学分类机器学习K近邻
importnumpyasnpimportpandasaspdfromsklearn.datasetsimportload_irisfromsklearn.model_selectionimporttrain_test_splitfromsklearn.metricsimportaccuracy_score1.数据预处理iris=load_iris()df=pd.DataFrame(data=ir
- 数据结构 | 栈和队列
TT-Kun
数据结构与算法数据结构栈队列C语言
文章目录栈和队列1.栈:后进先出(LIFO)的数据结构1.1概念与结构1.2栈的实现2.队列:先进先出(FIFO)的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中,栈和队列是两种基本且重要的数据结构,它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
- [Python] 数据结构 详解及代码
AIAdvocate
算法python数据结构链表
今日内容大纲介绍数据结构介绍列表链表1.数据结构和算法简介程序大白话翻译,程序=数据结构+算法数据结构指的是存储,组织数据的方式.算法指的是为了解决实际业务问题而思考思路和方法,就叫:算法.2.算法的5大特性介绍算法具有独立性算法是解决问题的思路和方式,最重要的是思维,而不是语言,其(算法)可以通过多种语言进行演绎.5大特性有输入,需要传入1或者多个参数有输出,需要返回1个或者多个结果有穷性,执行
- Python算法L5:贪心算法
小熊同学哦
Python算法算法python贪心算法
Python贪心算法简介目录Python贪心算法简介贪心算法的基本步骤贪心算法的适用场景经典贪心算法问题1.**零钱兑换问题**2.**区间调度问题**3.**背包问题**贪心算法的优缺点优点:缺点:结语贪心算法(GreedyAlgorithm)是一种在每一步选择中都采取当前最优或最优解的算法。它的核心思想是,在保证每一步局部最优的情况下,希望通过贪心选择达到全局最优解。虽然贪心算法并不总能得到全
- 【RabbitMQ 项目】服务端:数据管理模块之绑定管理
月夜星辉雪
rabbitmq分布式
文章目录一.编写思路二.代码实践一.编写思路定义绑定信息类交换机名称队列名称绑定关键字:交换机的路由交换算法中会用到没有是否持久化的标志,因为绑定是否持久化取决于交换机和队列是否持久化,只有它们都持久化时绑定才需要持久化。绑定就好像一根绳子,两端连接着交换机和队列,当一方不存在,它就没有存在的必要了定义绑定持久化类构造函数:如果数据库文件不存在则创建,打开数据库,创建binding_table插入
- 非对称加密算法原理与应用2——RSA私钥加密文件
私语茶馆
云部署与开发架构及产品灵感记录RSA2048私钥加密
作者:私语茶馆1.相关章节(1)非对称加密算法原理与应用1——秘钥的生成-CSDN博客第一章节讲述的是创建秘钥对,并将公钥和私钥导出为文件格式存储。本章节继续讲如何利用私钥加密内容,包括从密钥库或文件中读取私钥,并用RSA算法加密文件和String。2.私钥加密的概述本文主要基于第一章节的RSA2048bit的非对称加密算法讲述如何利用私钥加密文件。这种加密后的文件,只能由该私钥对应的公钥来解密。
- 粒子群优化 (PSO) 在三维正弦波函数中的应用
subject625Ruben
机器学习人工智能matlab算法
在这篇博客中,我们将展示如何使用粒子群优化(PSO)算法求解三维正弦波函数,并通过增加正弦波扰动,使优化过程更加复杂和有趣。本文将介绍目标函数的定义、PSO参数设置以及算法执行的详细过程,并展示搜索空间中的动态过程和收敛曲线。1.目标函数定义我们使用的目标函数是一个三维正弦波函数,定义如下:objectiveFunc=@(x)sin(sqrt(x(1).^2+x(2).^2))+0.5*sin(5
- 非对称加密算法————RSA理论及详情
hu19930613
转自:https://www.kancloud.cn/kancloud/rsa_algorithm/48484一、一点历史1976年以前,所有的加密方法都是同一种模式:(1)甲方选择某一种加密规则,对信息进行加密;(2)乙方使用同一种规则,对信息进行解密。由于加密和解密使用同样规则(简称"密钥"),这被称为"对称加密算法"(Symmetric-keyalgorithm)。这种加密模式有一个最大弱点
- ai绘画工具midjourney怎么下载?附作品管理教程
设计师早上好
Midjourney是一款功能强大的AI绘画工具,它使用机器学习技术和深度神经网络等算法,可以生成各种艺术风格的绘画作品。在创意设计、广告宣传等方面有着广泛的应用前景。那么,ai绘画工具midjourney怎么下载?本文将为您介绍Midjourney的下载以及作品的相关管理。一、Midjourney下载Midjourney的下载非常简单,只需打开Midjourney官网(点击“GetMidjour
- 【加密算法基础——对称加密和非对称加密】
XWWW668899
网络安全服务器笔记
对称加密与非对称加密对称加密和非对称加密是两种基本的加密方法,各自有不同的特点和用途。以下是详细比较:1.对称加密特点密钥:使用相同的密钥进行加密和解密。发送方和接收方必须共享这个密钥。速度:通常速度较快,适合处理大量数据。实现:算法相对简单,计算效率高。常见算法AES(高级加密标准)DES(数据加密标准)3DES(三重数据加密标准)RC4(流密码)应用场景文件加密磁盘加密传输大量数据时的加密2.
- 【算法练习】IDEA集成leetcode插件实现快速刷
2401_84102892
2024年程序员学习算法intellij-idealeetcode
============点击右侧边leetcode->设置->配置地址、用户名、密码、存放目录、文件模板用户名要登录后在账号信息里看模板代码1.codefilename!velocityTool.camelC
- 【加密算法基础——RSA 加密】
XWWW668899
网络服务器笔记python
RSA加密RSA(Rivest-Shamir-Adleman)加密是非对称加密,一种广泛使用的公钥加密算法,主要用于安全数据传输。公钥用于加密,私钥用于解密。RSA加密算法的名称来源于其三位发明者的姓氏:R:RonRivestS:AdiShamirA:LeonardAdleman这三位计算机科学家在1977年共同提出了这一算法,并发表了相关论文。他们的工作为公钥加密的基础奠定了重要基础,使得安全通
- 机器学习-聚类算法
不良人龍木木
机器学习机器学习算法聚类
机器学习-聚类算法1.AHC2.K-means3.SC4.MCL仅个人笔记,感谢点赞关注!1.AHC2.K-means3.SC传统谱聚类:个人对谱聚类算法的理解以及改进4.MCL目前仅专注于NLP的技术学习和分享感谢大家的关注与支持!
- 生成式地图制图
Bwywb_3
深度学习机器学习深度学习生成对抗网络
生成式地图制图(GenerativeCartography)是一种利用生成式算法和人工智能技术自动创建地图的技术。它结合了传统的地理信息系统(GIS)技术与现代生成模型(如深度学习、GANs等),能够根据输入的数据自动生成符合需求的地图。这种方法在城市规划、虚拟环境设计、游戏开发等多个领域具有应用前景。主要特点:自动化生成:通过算法和模型,系统能够根据输入的地理或空间数据自动生成地图,而无需人工逐
- 高性能javascript--算法和流程控制
海淀萌狗
-for,while和do-while性能相当-避免使用for-in循环,==除非遍历一个属性量未知的对象==es5:for-in遍历的对象便不局限于数组,还可以遍历对象。原因:for-in每次迭代操作会同时搜索实例或者原型属性,for-in循环的每次迭代都会产生更多开销,因此要比其他循环类型慢,一般速度为其他类型循环的1/7。因此,除非明确需要迭代一个属性数量未知的对象,否则应避免使用for-i
- 深度 Qlearning:在直播推荐系统中的应用
AGI通用人工智能之禅
程序员提升自我硅基计算碳基计算认知计算生物计算深度学习神经网络大数据AIGCAGILLMJavaPython架构设计Agent程序员实现财富自由
深度Q-learning:在直播推荐系统中的应用关键词:深度Q-learning,强化学习,直播推荐系统,个性化推荐1.背景介绍1.1问题的由来随着互联网技术的飞速发展,直播平台如雨后春笋般涌现。面对海量的直播内容,用户很难快速找到自己感兴趣的内容。因此,个性化推荐系统在直播平台中扮演着越来越重要的角色。1.2研究现状目前,主流的个性化推荐算法包括协同过滤、基于内容的推荐等。这些方法在一定程度上缓
- JVM源码分析之堆外内存完全解读
HeapDump性能社区
概述广义的堆外内存说到堆外内存,那大家肯定想到堆内内存,这也是我们大家接触最多的,我们在jvm参数里通常设置-Xmx来指定我们的堆的最大值,不过这还不是我们理解的Java堆,-Xmx的值是新生代和老生代的和的最大值,我们在jvm参数里通常还会加一个参数-XX:MaxPermSize来指定持久代的最大值,那么我们认识的Java堆的最大值其实是-Xmx和-XX:MaxPermSize的总和,在分代算法
- 《算法》四学习——1.1节
进阶的Farmer
算法算法笔记
前言买了一本算法4,每天看一点,对每个小结来个学习总结,输出驱动输入。本篇笔记针对第一章基础1.1基础编程模型1.1节总结了相关的语法、语言特性和书中将会用到的库。笔记自己在编码中容易遗漏的点&&优先级比||高在开发中习惯了加括号,所以没注意到这点,教材上也有但是忘记了二分查找中计算mid=left+(right-left)/2这样计算可以有效避免(left+right)/2溢出答疑java无穷大
- 排序
路小白同学
1.冒泡排序冒泡算法是一种基础的排序算法,这种算法会重复的比较数组中相邻的两个元素。如果一个元素比另一个元素大(小),那么就交换这两个元素的位置。重复这一比较直至最后一个元素。这一比较会重复n-1趟,每一趟比较n-j次,j是已经排序好的元素个数。每一趟比较都能找出未排序元素中最大或者最小的那个数字。这就如同水泡从水底逐个飘到水面一样。冒泡排序是一种时间复杂度较高,效率较低的排序方法。其空间复杂度是
- ztree异步加载
3213213333332132
JavaScriptAjaxjsonWebztree
相信新手用ztree的时候,对异步加载会有些困惑,我开始的时候也是看了API花了些时间才搞定了异步加载,在这里分享给大家。
我后台代码生成的是json格式的数据,数据大家按各自的需求生成,这里只给出前端的代码。
设置setting,这里只关注async属性的配置
var setting = {
//异步加载配置
- thirft rpc 具体调用流程
BlueSkator
中间件rpcthrift
Thrift调用过程中,Thrift客户端和服务器之间主要用到传输层类、协议层类和处理类三个主要的核心类,这三个类的相互协作共同完成rpc的整个调用过程。在调用过程中将按照以下顺序进行协同工作:
(1) 将客户端程序调用的函数名和参数传递给协议层(TProtocol),协议
- 异或运算推导, 交换数据
dcj3sjt126com
PHP异或^
/*
* 5 0101
* 9 1010
*
* 5 ^ 5
* 0101
* 0101
* -----
* 0000
* 得出第一个规律: 相同的数进行异或, 结果是0
*
* 9 ^ 5 ^ 6
* 1010
* 0101
* ----
* 1111
*
* 1111
* 0110
* ----
* 1001
- 事件源对象
周华华
JavaScript
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml&q
- MySql配置及相关命令
g21121
mysql
MySQL安装完毕后我们需要对它进行一些设置及性能优化,主要包括字符集设置,启动设置,连接优化,表优化,分区优化等等。
一 修改MySQL密码及用户
- [简单]poi删除excel 2007超链接
53873039oycg
Excel
采用解析sheet.xml方式删除超链接,缺点是要打开文件2次,代码如下:
public void removeExcel2007AllHyperLink(String filePath) throws Exception {
OPCPackage ocPkg = OPCPac
- Struts2添加 open flash chart
云端月影
准备以下开源项目:
1. Struts 2.1.6
2. Open Flash Chart 2 Version 2 Lug Wyrm Charmer (28th, July 2009)
3. jofc2,这东西不知道是没做好还是什么意思,好像和ofc2不怎么匹配,最好下源码,有什么问题直接改。
4. log4j
用eclipse新建动态网站,取名OFC2Demo,将Struts2 l
- spring包详解
aijuans
spring
下载的spring包中文件及各种包众多,在项目中往往只有部分是我们必须的,如果不清楚什么时候需要什么包的话,看看下面就知道了。 aspectj目录下是在Spring框架下使用aspectj的源代码和测试程序文件。Aspectj是java最早的提供AOP的应用框架。 dist 目录下是Spring 的发布包,关于发布包下面会详细进行说明。 docs&nb
- 网站推广之seo概念
antonyup_2006
算法Web应用服务器搜索引擎Google
持续开发一年多的b2c网站终于在08年10月23日上线了。作为开发人员的我在修改bug的同时,准备了解下网站的推广分析策略。
所谓网站推广,目的在于让尽可能多的潜在用户了解并访问网站,通过网站获得有关产品和服务等信息,为最终形成购买决策提供支持。
网站推广策略有很多,seo,email,adv
- 单例模式,sql注入,序列
百合不是茶
单例模式序列sql注入预编译
序列在前面写过有关的博客,也有过总结,但是今天在做一个JDBC操作数据库的相关内容时 需要使用序列创建一个自增长的字段 居然不会了,所以将序列写在本篇的前面
1,序列是一个保存数据连续的增长的一种方式;
序列的创建;
CREATE SEQUENCE seq_pro
2 INCREMENT BY 1 -- 每次加几个
3
- Mockito单元测试实例
bijian1013
单元测试mockito
Mockito单元测试实例:
public class SettingServiceTest {
private List<PersonDTO> personList = new ArrayList<PersonDTO>();
@InjectMocks
private SettingPojoService settin
- 精通Oracle10编程SQL(9)使用游标
bijian1013
oracle数据库plsql
/*
*使用游标
*/
--显示游标
--在显式游标中使用FETCH...INTO语句
DECLARE
CURSOR emp_cursor is
select ename,sal from emp where deptno=1;
v_ename emp.ename%TYPE;
v_sal emp.sal%TYPE;
begin
ope
- 【Java语言】动态代理
bit1129
java语言
JDK接口动态代理
JDK自带的动态代理通过动态的根据接口生成字节码(实现接口的一个具体类)的方式,为接口的实现类提供代理。被代理的对象和代理对象通过InvocationHandler建立关联
package com.tom;
import com.tom.model.User;
import com.tom.service.IUserService;
- Java通信之URL通信基础
白糖_
javajdkwebservice网络协议ITeye
java对网络通信以及提供了比较全面的jdk支持,java.net包能让程序员直接在程序中实现网络通信。
在技术日新月异的现在,我们能通过很多方式实现数据通信,比如webservice、url通信、socket通信等等,今天简单介绍下URL通信。
学习准备:建议首先学习java的IO基础知识
URL是统一资源定位器的简写,URL可以访问Internet和www,可以通过url
- 博弈Java讲义 - Java线程同步 (1)
boyitech
java多线程同步锁
在并发编程中经常会碰到多个执行线程共享资源的问题。例如多个线程同时读写文件,共用数据库连接,全局的计数器等。如果不处理好多线程之间的同步问题很容易引起状态不一致或者其他的错误。
同步不仅可以阻止一个线程看到对象处于不一致的状态,它还可以保证进入同步方法或者块的每个线程,都看到由同一锁保护的之前所有的修改结果。处理同步的关键就是要正确的识别临界条件(cri
- java-给定字符串,删除开始和结尾处的空格,并将中间的多个连续的空格合并成一个。
bylijinnan
java
public class DeleteExtraSpace {
/**
* 题目:给定字符串,删除开始和结尾处的空格,并将中间的多个连续的空格合并成一个。
* 方法1.用已有的String类的trim和replaceAll方法
* 方法2.全部用正则表达式,这个我不熟
* 方法3.“重新发明轮子”,从头遍历一次
*/
public static v
- An error has occurred.See the log file错误解决!
Kai_Ge
MyEclipse
今天早上打开MyEclipse时,自动关闭!弹出An error has occurred.See the log file错误提示!
很郁闷昨天启动和关闭还好着!!!打开几次依然报此错误,确定不是眼花了!
打开日志文件!找到当日错误文件内容:
--------------------------------------------------------------------------
- [矿业与工业]修建一个空间矿床开采站要多少钱?
comsci
地球上的钛金属矿藏已经接近枯竭...........
我们在冥王星的一颗卫星上面发现一些具有开采价值的矿床.....
那么,现在要编制一个预算,提交给财政部门..
- 解析Google Map Routes
dai_lm
google api
为了获得从A点到B点的路劲,经常会使用Google提供的API,例如
[url]
http://maps.googleapis.com/maps/api/directions/json?origin=40.7144,-74.0060&destination=47.6063,-122.3204&sensor=false
[/url]
从返回的结果上,大致可以了解应该怎么走,但
- SQL还有多少“理所应当”?
datamachine
sql
转贴存档,原帖地址:http://blog.chinaunix.net/uid-29242841-id-3968998.html、http://blog.chinaunix.net/uid-29242841-id-3971046.html!
------------------------------------华丽的分割线--------------------------------
- Yii使用Ajax验证时,如何设置某些字段不需要验证
dcj3sjt126com
Ajaxyii
经常像你注册页面,你可能非常希望只需要Ajax去验证用户名和Email,而不需要使用Ajax再去验证密码,默认如果你使用Yii 内置的ajax验证Form,例如:
$form=$this->beginWidget('CActiveForm', array( 'id'=>'usuario-form',&
- 使用git同步网站代码
dcj3sjt126com
crontabgit
转自:http://ued.ctrip.com/blog/?p=3646?tn=gongxinjun.com
管理一网站,最开始使用的虚拟空间,采用提供商支持的ftp上传网站文件,后换用vps,vps可以自己搭建ftp的,但是懒得搞,直接使用scp传输文件到服务器,现在需要更新文件到服务器,使用scp真的很烦。发现本人就职的公司,采用的git+rsync的方式来管理、同步代码,遂
- sql基本操作
蕃薯耀
sqlsql基本操作sql常用操作
sql基本操作
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
蕃薯耀 2015年6月1日 17:30:33 星期一
&
- Spring4+Hibernate4+Atomikos3.3多数据源事务管理
hanqunfeng
Hibernate4
Spring3+后不再对JTOM提供支持,所以可以改用Atomikos管理多数据源事务。Spring2.5+Hibernate3+JTOM参考:http://hanqunfeng.iteye.com/blog/1554251Atomikos官网网站:http://www.atomikos.com/ 一.pom.xml
<dependency>
<
- jquery中两个值得注意的方法one()和trigger()方法
jackyrong
trigger
在jquery中,有两个值得注意但容易忽视的方法,分别是one()方法和trigger()方法,这是从国内作者<<jquery权威指南》一书中看到不错的介绍
1) one方法
one方法的功能是让所选定的元素绑定一个仅触发一次的处理函数,格式为
one(type,${data},fn)
&nb
- 拿工资不仅仅是让你写代码的
lampcy
工作面试咨询
这是我对团队每个新进员工说的第一件事情。这句话的意思是,我并不关心你是如何快速完成任务的,哪怕代码很差,只要它像救生艇通气门一样管用就行。这句话也是我最喜欢的座右铭之一。
这个说法其实很合理:我们的工作是思考客户提出的问题,然后制定解决方案。思考第一,代码第二,公司请我们的最终目的不是写代码,而是想出解决方案。
话粗理不粗。
付你薪水不是让你来思考的,也不是让你来写代码的,你的目的是交付产品
- 架构师之对象操作----------对象的效率复制和判断是否全为空
nannan408
架构师
1.前言。
如题。
2.代码。
(1)对象的复制,比spring的beanCopier在大并发下效率要高,利用net.sf.cglib.beans.BeanCopier
Src src=new Src();
BeanCopier beanCopier = BeanCopier.create(Src.class, Des.class, false);
- ajax 被缓存的解决方案
Rainbow702
JavaScriptjqueryAjaxcache缓存
使用jquery的ajax来发送请求进行局部刷新画面,各位可能都做过。
今天碰到一个奇怪的现象,就是,同一个ajax请求,在chrome中,不论发送多少次,都可以发送至服务器端,而不会被缓存。但是,换成在IE下的时候,发现,同一个ajax请求,会发生被缓存的情况,只有第一次才会被发送至服务器端,之后的不会再被发送。郁闷。
解决方法如下:
① 直接使用 JQuery提供的 “cache”参数,
- 修改date.toLocaleString()的警告
tntxia
String
我们在写程序的时候,经常要查看时间,所以我们经常会用到date.toLocaleString(),但是date.toLocaleString()是一个过时 的API,代替的方法如下:
package com.tntxia.htmlmaker.util;
import java.text.SimpleDateFormat;
import java.util.
- 项目完成后的小总结
xiaomiya
js总结项目
项目完成了,突然想做个总结但是有点无从下手了。
做之前对于客户端给的接口很模式。然而定义好了格式要求就如此的愉快了。
先说说项目主要实现的功能吧
1,按键精灵
2,获取行情数据
3,各种input输入条件判断
4,发送数据(有json格式和string格式)
5,获取预警条件列表和预警结果列表,
6,排序,
7,预警结果分页获取
8,导出文件(excel,text等)
9,修
![]() 个观测样本
个观测样本![]() ,每个样本都包含
,每个样本都包含![]() 个特征
个特征![]() 二元分类不同,将负类设为
二元分类不同,将负类设为![]() ,正类不变,为
,正类不变,为![]() 。当用线性的决策边界去划分两类时,
。当用线性的决策边界去划分两类时,![]() 时,
时,![]()
![]() 时,
时,![]()
![]()
![]() ,即夹在两条决策边界中间的直线。为了达到最佳的分类效果,要使两条决策边界之间的距离最大,而两类之间的距离由最靠近边界的点决定,即
,即夹在两条决策边界中间的直线。为了达到最佳的分类效果,要使两条决策边界之间的距离最大,而两类之间的距离由最靠近边界的点决定,即![]() 与
与![]() 来决定,即最大距离
来决定,即最大距离![]() 为
为![]()
![]() 为松驰项,表示允许有一些样本在边界外,但是不能过多,因此需要使
为松驰项,表示允许有一些样本在边界外,但是不能过多,因此需要使![]() 和
和![]() 需要取得最大值,即
需要取得最大值,即![]() 。
。 ![]() 求偏导数为
求偏导数为![]() 都取得最大值,利用SMO算法(Sequential minimal optimization),每次变动两个参数,与此同时固定其余所有的参数。之所以选择变动两个参数,是因为有限制条件
都取得最大值,利用SMO算法(Sequential minimal optimization),每次变动两个参数,与此同时固定其余所有的参数。之所以选择变动两个参数,是因为有限制条件![]() 分成两个部分,一部分包含了变动参数
分成两个部分,一部分包含了变动参数![]() ,另一部分与变动参数无关,将其他参数
,另一部分与变动参数无关,将其他参数![]() 看做是一个常数。
看做是一个常数。![]() 为
为![]() 为
为![]() 式可以用
式可以用![]() 来表示
来表示![]()
![]() ,所以
,所以![]() 也可以表示为
也可以表示为![]()
![]() 代入
代入![]() 式,记
式,记![]() ,可得
,可得因为
![]() ,所以它们的平方项都为
,所以它们的平方项都为![]() ,故
,故![]() 化简可得
化简可得化简为标准型为
![]() 可知
可知![]() 为开口向下的抛物线,在不考虑
为开口向下的抛物线,在不考虑![]() 的情况下,
的情况下,![]() 取得极大值所对应的
取得极大值所对应的![]() 为
为![]() 式带入可得
式带入可得![]() 可以化简为
可以化简为![]() ,式子的左边为新的
,式子的左边为新的![]() ,因此这个式子可以用来更新
,因此这个式子可以用来更新![]() 。现在加入之前没有考虑的约束条件:
。现在加入之前没有考虑的约束条件:![]()
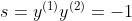 时
时![]() 可以得出
可以得出![]()
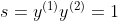 时
时![]() 可以得出
可以得出![]()
![]() 落在上述区间内,那么就取
落在上述区间内,那么就取![]() ;如果
;如果![]() 小于所允许的最小值,那么
小于所允许的最小值,那么 ![]() ; 如果
; 如果![]() 大于所允许的最大值,那么
大于所允许的最大值,那么![]() 。
。 ![]() ,我们就可以算出新的
,我们就可以算出新的![]() 。 如果
。 如果![]() 按之前的规则取值,那么我们就可以保证
按之前的规则取值,那么我们就可以保证![]() 一定会落在有效区间之内。
一定会落在有效区间之内。 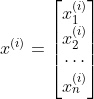




![\lambda ^{(i)}\geqslant 0 \ , \ \sum_{i=1}^{m}\lambda ^{(i)}\left [1-\xi ^{(i)}-y^{(i)}\left (w ^{T}x^{(i)}+b \right )\right ]\leqslant 0](http://img.e-com-net.com/image/info8/0fe4848576c946fdb10b021562297263.gif)