【路径规划】基于灰狼算法求解旅行商TSP问题matlab源码
一、旅行商问题
TSP问题即旅行商问题，经典的TSP可以描述为：一个商品推销员要去若干个城市推销商品，该推销员从一个城市出发，需要经过所有城市后，回到出发地。应如何选择行进路线，以使总的行程最短。从图论的角度来看，该问题实质是在一个带权完全无向图中，找一个权值最小的哈密尔顿回路。
旅行商问题有很多种不同的问法，最近做了几个关于TSP的题，下面总结一下。由于大部分TSP问题都是NP-Hard的，因此很难得到什么高效的多项式级别的算法，一般采用的算法都偏向于暴力搜索以及状压DP，这里都采取用状压DP解决。大部分TSP问题所给的地点数目都非常小。
考虑经典的TSP问题，如果采用状压DP，将每个地点访问与否作为二进制1/0压缩，不难得到状态转移方程：
dp[S][i] = min(dp[S][i], dp[S ^ (1 << (i - 1))][k] + dist[k][i])
S代表当前状态，i(从1开始)表示到达当前状态时最后访问的是第i个地点
k为S中所有访问的与i不同的地点。
dist表示两点间最短路。
以及初始化：
DP[S][i] = dist[start][i](S == 1<<(i - 1))
如果初次遇到状压dp，感到陌生的话，就请仔细思考上面式子的含义，这是大部分TSP问题的关键。
二、灰狼算法
1、灰狼优化算法
灰狼隶属于群居生活的犬科动物，且处于食物链的顶层。灰狼严格遵守着一个社会支配等级关系。如图：
社会等级第一层：狼群中的头狼记为 
， 狼主要负责对捕食、栖息、作息时间等活动作出决策。由于其它的狼需要服从 狼的命令，所以 狼也被称为支配狼。另外， 狼不一定是狼群中最强的狼，但就管理能力方面来说， 狼一定是最好的。
社会等级第二层：
狼，它服从于 狼，并协助 狼作出决策。在 狼去世或衰老后， 狼将成为 狼的最候选者。虽然 狼服从 狼，但 狼可支配其它社会层级上的狼。
社会等级第三层：
狼，它服从 、 狼，同时支配剩余层级的狼。 狼一般由幼狼、哨兵狼、狩猎狼、老年狼及护理狼组成。
社会等级第四层：
狼，它通常需要服从其它社会层次上的狼。虽然看上去 狼在狼群中的作用不大，但是如果没有 狼的存在，狼群会出现内部问题如自相残杀。
GWO 优化过程包含了灰狼的社会等级分层、跟踪、包围和攻击猎物等步骤，其步骤具体情况如下所示。
１）社会等级分层（Social Hierarchy）当设计 GWO 时，首先需构建灰狼社会等级层次模型。计算种群每个个体的适应度，将狼群中适应度最好的三匹灰狼依次标记为 、 、 ，而剩下的灰狼标记为 。也就是说，灰狼群体中的社会等级从高往低排列依次为； 、 、 及 。GWO 的优化过程主要由每代种群中的最好三个解（即 、 、 ）来指导完成。
２）包围猎物（ Encircling Prey ）灰狼捜索猎物时会逐渐地接近猎物并包围它，该行为的数学模型如下：
式中：t 为当前迭代次数：。表示 hadamard 乘积操作；A 和 C 是协同系数向量；Xp 表示猎物的位置向量； X(t) 表示当前灰狼的位置向量；在整个迭代过程中 a 由2 线性降到 0； r1 和 r2 是 [0，1] 中的随机向量。
３）狩猎（ Hunring）
灰狼具有识别潜在猎物（最优解）位置的能力，搜索过程主要靠 、 、 灰狼的指引来完成。但是很多问题的解空间特征是未知的，灰狼是无法确定猎物（最优解）的精确位置。为了模拟灰狼（候选解）的搜索行为，假设 、 、 具有较强识别潜在猎物位置的能力。因此，在每次迭代过程中，保留当前种群中的最好三只灰狼（ 、 、 ），然后根据它们的位置信息来更新其它搜索代理（包括 ）的位置。该行为的数学模型可表示如下：
式中：
、
、
分别表示当前种群中 、 、 的位置向量；Ｘ表示灰狼的位置向量；
、
、
分别表示当前候选灰狼与最优三条狼之间的距离；当｜A｜＞１时，灰狼之间尽量分散在各区域并搜寻猎物。当｜A｜＜１时，灰狼将集中捜索某个或某些区域的猎物。
从图中可看出，候选解的位置最终落在被 、 、 定义的随机圆位置内。总的来说， 、 、 需首先预测出猎物（潜 在最优解）的大致位置，然后其它候选狼在当前最优兰只狼的指引下在猎物附近随机地更新它们的位置。
４）攻击猎物（Attacking Prey）构建攻击猎物模型的过程中，根据2)中的公式，ａ值的减少会引起 A 的值也随之波动。换句话说，A 是一个在区间［-a，a］（备注：原作者的第一篇论文里这里是[-2a,2a]，后面论文里纠正为[-a,a]）上的随机向量，其中ａ在迭代过程中呈线性下降。当 A 在［-1，１］区间上时，则捜索代理（Search Agent）的下一时刻位置可以在当前灰狼与猎物之间的任何位置上。
５）寻找猎物（Search for Prey）灰狼主要依赖 、 、 的信息来寻找猎物。它们开始分散地去搜索猎物位置信息，然后集中起来攻击猎物。对于分散模型的建立，通过｜A｜＞１使其捜索代理远离猎物，这种搜索方式使 GWO 能进行全局搜索。GWO 算法中的另一个搜索系数是Ｃ。从2)中的公式可知，Ｃ向量是在区间范围［０，２］上的随机值构成的向量，此系数为猎物提供了随机权重，以便増加（｜Ｃ｜＞１）或减少（｜Ｃ｜＜１）。这有助于 GWO 在优化过程中展示出随机搜索行为，以避免算法陷入局部最优。值得注意的是，Ｃ并不是线性下降的，Ｃ在迭代过程中是随机值，该系数有利于算法跳出局部，特别是算法在迭代的后期显得尤为重要。
2.算法流程图
流程图
三、部分代码
clc;
clear;
%% TSP问题设置
% 产生问题模型
model = CreateModel('Oliver30.txt');
% 城市分布图
figure(1);
plot(model.x, model.y, 'ms', 'LineWidth', 2, 'MarkerEdgeColor', 'k', 'MarkerFaceColor', 'g')
legend('城市位置')
title('城市分布图', 'fontsize', 12)
xlabel('km', 'fontsize', 12)
ylabel('km', 'fontsize', 12)
grid on
% 适应度函数句柄
Fun = @(tour) TourLength(tour, model);
% TSP参数
M = model.n; % 城市个数
% GWO参数
N = 50; % 灰狼个数
Max_iter = 1000; % 最大迭代次数
lb = -10; % Lower Bound
ub = 10; % Upper Bound
dim = M; % 维数
% 初始化alpha, beta, and delta_pos
Alpha_pos = zeros(1,dim);
Alpha_score = inf;
Beta_pos = zeros(1,dim);
Beta_score = inf;
Delta_pos = zeros(1,dim);
Delta_score = inf;
% 初始化种群位置
Positions = rand(N, dim).*(ub-lb)+lb;
Length_best = zeros(1, Max_iter);
Length_ave = zeros(1, Max_iter);
l = 1; % 迭代计数器
%% 迭代寻优
while l < Max_iter+1
Positions(i, j) = (X1+X2+X3)/3; % Equation (3.7)
end
end
Length_best(l) = Alpha_score; % 最短距离
Length_ave(l) = Length_ave(l)/dim; % 平均距离
disp(['Iteration ' num2str(l) ': Best Fitness = ' num2str(Alpha_score)]);
l = l + 1;
[~, BestSol] = sort(Alpha_pos);
figure(2);
PlotSolution(BestSol, model, Alpha_score);
pause(0.01);
end
%% 进化曲线
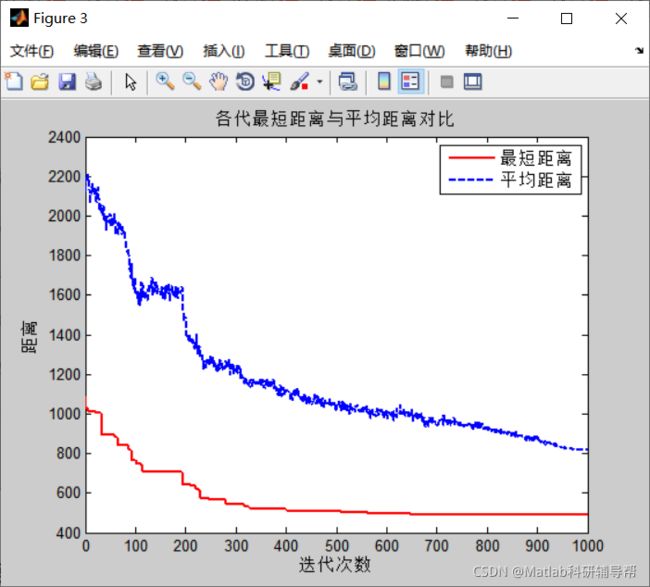
figure(3);
t = 1:Max_iter;
plot(t, Length_best, 'r', t, Length_ave, 'b--', 'LineWidth', 2);
xlabel('Iteration');
ylabel('Best Cost');
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')四、仿真结果
五、参考文献
[1]高珊,孟亮.贪婪随机自适应灰狼优化算法求解TSP问题[J].现代电子技术,2019,42(14):46-50+54.
