为什么正则化能够解决过拟合问题?
为什么正则化能够解决过拟合问题
- 一. 正则化的解释
- 二. 拉格朗日乘数法
- 三. 正则化是怎么解决过拟合问题的
-
- 1. 引出范数
-
- 1.1 L_0范数
- 1.2 L_1范数
- 1.3 L_2范数
- 2. L_2范式正则项如何解决过拟合问题
-
- 2.1 公式推导
- 2.2 图像推导[^2]
-
- 2.2.1 L1正则化
- 2.2.2 L2正则化
- 四. 结论
如果觉得不想看前两大点,可以直接看第三点公式推导或图像观察,个人觉得特别好理解。
一. 正则化的解释
为防止模型过拟合,提高模型的泛化能力,通常会在损失函数的后面添加一个正则化项。
L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓惩罚是指对损失函数中的某些参数做一些约束, 使得参数的自由度变小。
正则化在深度学习中含义是指什么?正则化其实是一种策略
以增大训练误差为代价来减少测试误差的所有策略我们都可以称作为正则化。换句话说就是正则化是为了防止模型过拟合。L2范数就是最常用的正则化方法之一。1
二. 拉格朗日乘数法
为什么引出拉格朗日乘数法呢?因为就是这么巧,原理真的是特别像!
拉格朗日乘数法1
拉格朗日乘数法2
因为有很多人已经写过一遍了,找了两篇比较易懂的链接
这两个链接任看一个即可,大概想起来他的含义就可直接看第三点。
三. 正则化是怎么解决过拟合问题的
1. 引出范数
1.1 L_0范数
求出向量中非零元素的个数.
如果用L0规则化一个参数矩阵W,就是希望W中大部分元素是零,实现稀疏。
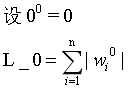
L0范数的应用:
1)特征选择
实现特征的自动选择,去除无用特征。稀疏化可以去掉这些无用特征,将特征对应的权重置为零。
2)可解释性(interpretability)
例如判断某种病的患病率时,最初有1000个特征,建模后参数经过稀疏化,最终只有5个特征的参数是非零的,那么就可以说影响患病率的主要就是这5个特征。
1.2 L_1范数
是指向量中各个元素的绝对值之和,也叫"系数规则算子(Lasso regularization)"。
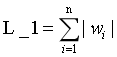
L1范数也可以实现稀疏,通过将无用特征对应的参数W置为零实现。
L0和L1都可以实现稀疏化,不过一般选用L1而不用L0,原因包括:
- L0范数很难优化求解(NP难);
- L1是L0的最优凸近似,比L0更容易优化求解。
1.3 L_2范数
L2范数的定义其实是一个数学概念,其定义如下:

这个公式看着相当熟悉吧,用的最多的欧式距离就是一种L2范数,表示向量元素的平方和再开方。
2. L_2范式正则项如何解决过拟合问题
有两种方式:
- 一种公式推导,
- 一种是图像观察
2.1 公式推导
那就让我们直接推导公式证明一下吧!
个人觉得能推导,就别描述,说不清楚,哈哈哈哈!
设模型函数为 :
![]()
W1、W2分别表示两个自变量的权重, 引入L2正则项之前,我们的损失函数为:
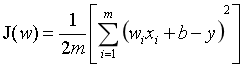
引入L2正则项之后:
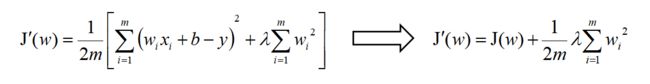
为什么它会使得我们的权重减小呢!
求偏导试试看,但是我们这里只有两个参数W1、W2,求偏导结果过如下:

可以发现,添加正则项之后,w相比原来在减小,即靠近0
2.2 图像推导2
2.2.1 L1正则化
设有如下带L1正则项的损失函数:

其中J0是原始的损失函数,加号后面的一项是L1正则化项,α是正则化系数。注意到L1正则化是权值的绝对值之和,J是带有绝对值符号的函数,因此J是不完全可微的。机器学习的任务就是要通过一些方法(比如梯度下降)求出损失函数的最小值。
当我们在原始损失函数J0后添加L1正则化项时,相当于对J0做了一个约束。令 L = α ∑ ∣ w ∣ L=α∑∣w∣ L=α∑∣w∣ ,则 J = J 0 + L J = J0+L J=J0+L此时我们的任务变成在 L L L约束下求出 J 0 J0 J0取最小值的解。(来啦来啦,有条件求极值——拉格朗日乘数法,是不是原理一模一样)3
考虑二维的情况,即只有两个权值 w 1 w 2 w^1w^2 w1w2,此时 L = ∣ w 1 ∣ + ∣ w 2 ∣ L = |w^1|+|w^2| L=∣w1∣+∣w2∣对于梯度下降法,求解 J 0 J0 J0 的过程可以画出等值线,同时 L 1 L1 L1正则化的函数 L L L也可以在 w 1 w 2 w^1w^2 w1w2 的二维平面上画出来。
如下图:

图中等值线是 J 0 J0 J0的等值线,黑色方形是 L L L函数的图形。在图中,当 J 0 J0 J0等值线与 L L L图形首次相交的地方就是最优解。上图中 J 0 J0 J0 与 L L L在 L L L的一个顶点处相交,这个顶点就是最优解。
注意到这个顶点的值是 ( w 1 , w 2 ) = ( 0 , w ) (w^1, w^2) = (0, w) (w1,w2)=(0,w)。可以直观想象,因为 L L L函数有很多棱角(二维情况下四个,多维情况下更多), J 0 J0 J0 与这些角接触的机率会远大于与 L L L其它部位接触的机率,而在这些角上,会有很多权值等于0
这就是为什么L1正则化可以产生稀疏模型,进而可以用于特征选择。
而正则化前面的系数 α α α,可以控制 L L L图形的大小。 α α α越小, L L L的图形越大(上图中的黑色方框); α α α越大, L L L的图形就越小,可以小到黑色方框只超出原点范围一点点,这是最优点的值 ( w 1 , w 2 ) = ( 0 , w ) (w^1, w^2) = (0, w) (w1,w2)=(0,w)中的 w w w可以取到很小的值。
2.2.2 L2正则化
设有如下带L2正则化的损失函数:

同样可以画出在二维平面上的图形,如下:

二维平面下 L 2 L2 L2正则化的函数图形是个圆,与方形相比,被磨去了棱角。因此 J 0 J0 J0与 L L L相交时使得 w 1 w1 w1或 w 2 w2 w2等于零的机率小了许多,这就是为什么L2正则化不具有稀疏性的原因。
四. 结论
相比添加正则项之前来说,添加了正则项之后,更新w参数将会使得w更小。
李宏毅4老师在他的课程有提到:函数的平滑性
w很小,意味着该function是一个比较平滑的函数
平滑性:对输入有较大变化,但是输出的变化很小,这该函数是一个平滑的function
而我们的model当然是更加平滑,那么稳定性就越好,那么当输入变化过大,预测的结果那么仍然保持保持高效,这和模型的泛化能力是不是就联系上了呢?
当然,以上仅为个人和前人的一点总结,可能个人说的会存在不好的地方。
大家可以在留言中call我,我会积极探讨,相互进步。
一文搞懂深度学习正则化的L2范数 ↩︎
机器学习中正则化项L1和L2的直观理解 ↩︎
拉格朗日乘数法 ↩︎
李宏毅老师课程b站链接提到平滑性 ↩︎