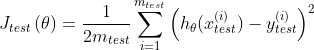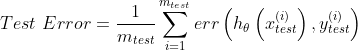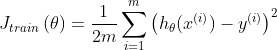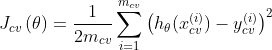机器学习诊断法
依然是以预测房价为例,假设我已经完成了正则化线性回归,也就是最小化代价函数![]()
并得到了使代价函数![]() 最小的参数
最小的参数![]() ,但将参数
,但将参数![]() 代入假设函数
代入假设函数![]() 并放到一组新的房屋样本上进行测试时,发现产生了巨大的误差,如果我想改进这个算法,我该怎做?假设有以下几种方法:
并放到一组新的房屋样本上进行测试时,发现产生了巨大的误差,如果我想改进这个算法,我该怎做?假设有以下几种方法:
- 使用更多的训练样本
- 减少特征向量
 的维度,既尝试使用更少的特征
的维度,既尝试使用更少的特征 - 增加特征向量
 的维度,既尝试使用更多的特征
的维度,既尝试使用更多的特征 - 增加多项式特征,既选用更复杂假设函数
 来拟合训练集(
来拟合训练集(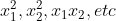 )
) - 增大正则化参数
 的值
的值 - 减小正则化参数
 的值
的值
我们该如何选择方法使模型能更好的拟合训练集和泛化?机器学习诊断法能够使我们了解该模型的问题出在哪,是高偏差还是高方差,采用什么方法去尝试才是有意义的。
1、评估假设
在判断假设函数![]() 是否过拟合时,如果特征较少,可以画出假设函数的图像,使用可视化的方式来判断,但对于一般情况来说,假设函数在特征较多时很难可视化。
是否过拟合时,如果特征较少,可以画出假设函数的图像,使用可视化的方式来判断,但对于一般情况来说,假设函数在特征较多时很难可视化。
可以把训练集划分为两部分,一部分为我们的训练集(Training Set),而另一部分为我们的测试集(Test Set)
![]()
一般按照![]() 来划分,如果训练集是有规律的话,最好是随机选择。
来划分,如果训练集是有规律的话,最好是随机选择。
这时就可以使用假设函数去拟合70%的数据,并最小化代价函数![]() ,并得到了使代价函数最小的参数
,并得到了使代价函数最小的参数![]() ,接下来要计算测试误差(Test Error),用
,接下来要计算测试误差(Test Error),用![]() 表示计算误差。
表示计算误差。
在回归问题中,不带正则项的![]() 为
为
而在分类问题中,不带正则项的![]() 为
为
比较![]() 和
和![]() 的值,如果两个值差距过大,则说明模型的泛化性较差。
的值,如果两个值差距过大,则说明模型的泛化性较差。
而对于分类问题,还有另一种计算测试误差的测量方法,叫做错误分类或者0/1错误分类
2、模型选择
2.1、训练集、交叉验证集、测试集
需要选择一个对数据集最合适的多项式次数,我应该选择一次函数,二次函数……十次函数中的哪一个
……
用参数![]() 来表示要选择的多项式的次数,可以依次选择模型来最小化训练代价函数
来表示要选择的多项式的次数,可以依次选择模型来最小化训练代价函数![]() ,得到参数向量
,得到参数向量![]() ,上标表示几次多项式的系数向量,然后将测试集代入依次计算
,上标表示几次多项式的系数向量,然后将测试集代入依次计算
![]()
选出其中使得测试误差![]() 最小的
最小的![]() ,既最好的拟合数据集的模型。假设此时选择
,既最好的拟合数据集的模型。假设此时选择![]() ,那么说明假设函数
,那么说明假设函数
![]()
对训练集的拟合程度最好。但是已经用了测试集去选择最合适多项式次数![]() ,再利用测试集去检测该模型的泛化程度显然过于乐观了,既选择的是最优的
,再利用测试集去检测该模型的泛化程度显然过于乐观了,既选择的是最优的![]() ,但该模型仍然有可能是过拟合的,对该测试集拟合效果好但对新样本来说并不一定,所以不能用训练集继续检验模型的泛化程度。
,但该模型仍然有可能是过拟合的,对该测试集拟合效果好但对新样本来说并不一定,所以不能用训练集继续检验模型的泛化程度。
所以把数据集分成训练集和测试集是不够的,需要分成三个部分,训练集,交叉验证集(Cross Validation Set)和测试集
![]()
一般按照![]() 来划分,如果训练集是有规律的话,最好是随机选择。
来划分,如果训练集是有规律的话,最好是随机选择。
这时就可以定义训练误差(Training Error)
验证误差(Cross Validation Error)
测试误差
训练误差就是最小化代价函数![]() 后,得到参数向量
后,得到参数向量![]() 后,再把训练集带入代价函数得到的(其实就是最小化的代价函数
后,再把训练集带入代价函数得到的(其实就是最小化的代价函数![]() ),而验证误差和测试误差是代入交叉训练集和测试集后得到的。
),而验证误差和测试误差是代入交叉训练集和测试集后得到的。
重复之前的步骤,次选择模型来最小化训练代价函数![]() ,得到参数向量
,得到参数向量![]() ,
,
然后将交叉训练集代入依次计算
![]()
选出其中使得交叉验证误差![]() 最小的
最小的![]() ,既最好的拟合数据集的模型,再将测试集的样本代入计算
,既最好的拟合数据集的模型,再将测试集的样本代入计算![]() ,衡量该模型的泛化误差。
,衡量该模型的泛化误差。
2.2、高偏差,高方差
当运行一个学习算法时,如果这个算法的表现并没有达到预期的效果,那么可能是两种情况,高偏差或者高误差,使用之前定义的训练误差和验证误差
绘制误差![]() ,既
,既![]() 和
和![]() 关于多项式次数
关于多项式次数![]() 的图像
的图像
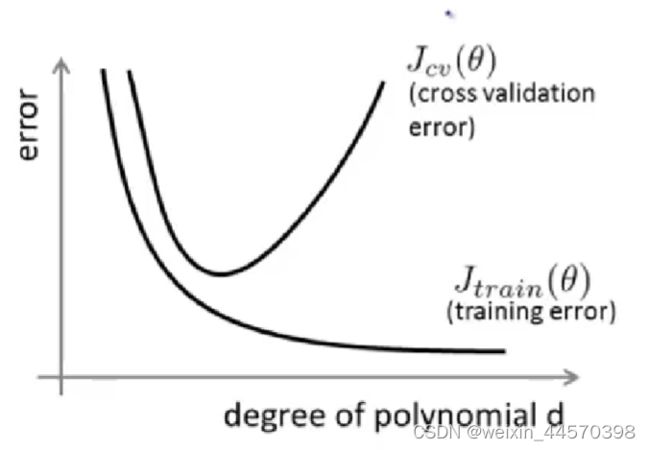
可以看到随着次数![]() 的增大,
的增大,![]() 减小,说明模型对训练集的拟合程度越好,但是随着次数
减小,说明模型对训练集的拟合程度越好,但是随着次数![]() 的增大,
的增大, ![]() 先减小后增大,说明随着次数
先减小后增大,说明随着次数![]() 的增大,模型越拟合数据,到了一定程度后,出现过拟合导致模型的误差增大,所以选择
的增大,模型越拟合数据,到了一定程度后,出现过拟合导致模型的误差增大,所以选择![]() 的最小值所对应的多项式次数
的最小值所对应的多项式次数![]() 。
。
而在![]() 的最小值的左边,对应的就是高偏差问题(欠拟合),此时
的最小值的左边,对应的就是高偏差问题(欠拟合),此时 ![]() 和
和![]() 都很大,而在右边出现的就是高方差问题(过拟合),此时
都很大,而在右边出现的就是高方差问题(过拟合),此时 ![]() 很小,但是
很小,但是![]() 很大,既
很大,既
- Bias(underfit)
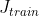 很大
很大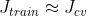
- Variance(overfit)
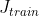 很小
很小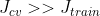
而正则化可以有效地防止过拟合,给代价函数加入正则项
正则化参数![]() 不能过大也不能过小,自动化的选择
不能过大也不能过小,自动化的选择![]() 的值
的值
……
同样最小化代价函数![]() ,得到参数向量
,得到参数向量![]() ,上标是选取正则化参数
,上标是选取正则化参数![]() 的个数,然后将交叉训练集代入依次计算
的个数,然后将交叉训练集代入依次计算
![]()
选出其中使得交叉验证误差![]() 最小的
最小的![]() ,既最好的拟合数据集的模型,再将测试集的样本代入计算
,既最好的拟合数据集的模型,再将测试集的样本代入计算![]() ,衡量该模型的泛化误差。
,衡量该模型的泛化误差。
绘制误差![]() ,既
,既![]() 和
和![]() 关于正则化参数
关于正则化参数![]() 的图像
的图像
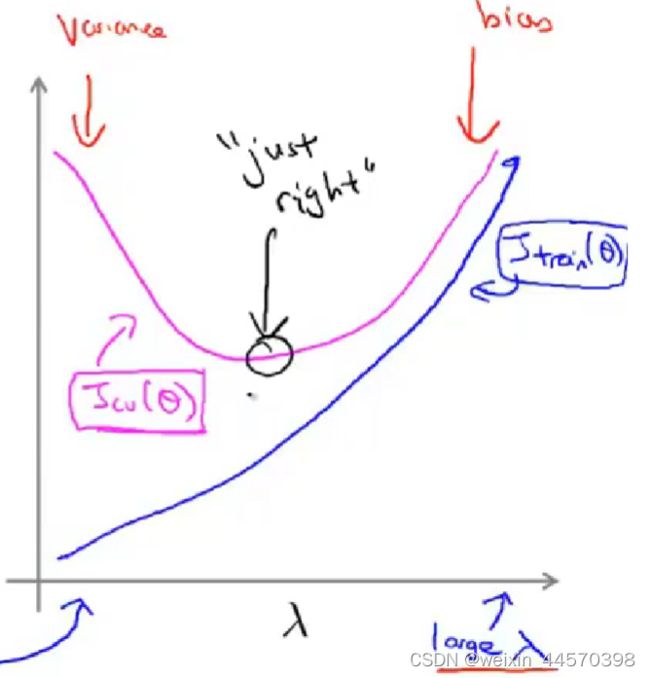
可以看到随着正则化参数![]() 的增大,
的增大,![]() 增大,说明模型一开始对训练集拟合程度很好,但随着
增大,说明模型一开始对训练集拟合程度很好,但随着![]() 的增大,使得
的增大,使得![]() ,逐渐变成一条直线,拟合程度变低。但是随着正则化参数
,逐渐变成一条直线,拟合程度变低。但是随着正则化参数![]() 的增大,
的增大, ![]() 先减小后增大,说明随着正则化参数
先减小后增大,说明随着正则化参数![]() 的增大,过拟合程度降低,到了一定程度后,出现欠拟合导致模型的误差增大,所以选择
的增大,过拟合程度降低,到了一定程度后,出现欠拟合导致模型的误差增大,所以选择![]() 的最小值所对应的正则化参数
的最小值所对应的正则化参数![]() 。
。
3、学习曲线
在高偏差时,绘制误差![]() ,既
,既![]() 和
和![]() 关于训练集中训练样本个数
关于训练集中训练样本个数![]() 的图像
的图像
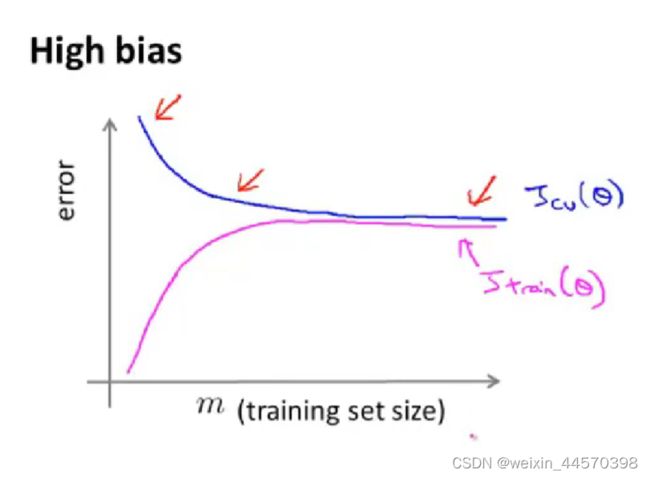
随着训练样本的增多,在欠拟合情况下,训练误差![]() 逐渐增大直至趋于平稳,因为当训练样本比较少的时候,或许还可以勉强拟合训练集,但随着训练样本的增加,训练误差会越大直至平稳。而验证误差
逐渐增大直至趋于平稳,因为当训练样本比较少的时候,或许还可以勉强拟合训练集,但随着训练样本的增加,训练误差会越大直至平稳。而验证误差![]() 会逐渐减小直至趋于平稳,并且最后
会逐渐减小直至趋于平稳,并且最后![]() 。
。
而在高方差时候, 绘制误差![]() ,既
,既![]() 和
和![]() 关于训练集中训练样本个数
关于训练集中训练样本个数![]() 的图像
的图像
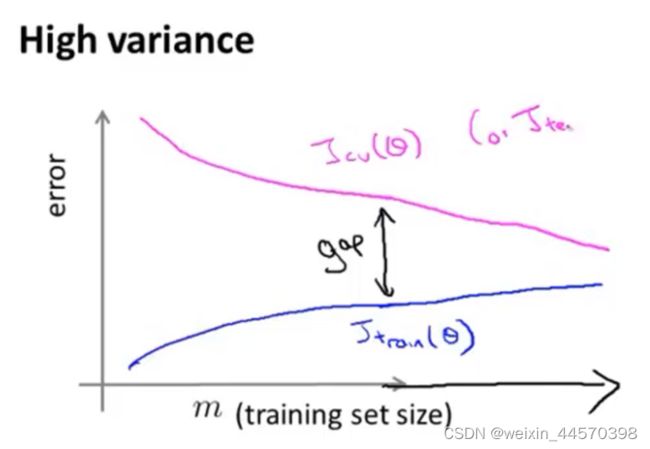
随着训练样本的增加,在过拟合情况下,训练误差![]() 逐渐增大直至趋于平稳。因为当训练样本比较少的时候,模型可以很好的拟合数据集,但随着训练样本的增加,就越难把训练集完全拟合,训练误差会增加直至平稳,但一直都处于较小的状态。而验证误差
逐渐增大直至趋于平稳。因为当训练样本比较少的时候,模型可以很好的拟合数据集,但随着训练样本的增加,就越难把训练集完全拟合,训练误差会增加直至平稳,但一直都处于较小的状态。而验证误差![]() 会逐渐减小直至趋于平稳,因为一开始过拟合,模型的泛化性很差,而随着训练样本的增加,过拟合的模型依旧很难泛化,所以
会逐渐减小直至趋于平稳,因为一开始过拟合,模型的泛化性很差,而随着训练样本的增加,过拟合的模型依旧很难泛化,所以![]() 和
和![]() 会有空隙,需要大量的数据集去解决这个问题。直至最后
会有空隙,需要大量的数据集去解决这个问题。直至最后![]() 。
。
因此对于最开始提出的改进算法的方法
- 使用更多的训练样本 ———— 在高方差的时候使用
- 减少特征向量
 的维度,既尝试使用更少的特征 ———— 在高方差的时候使用
的维度,既尝试使用更少的特征 ———— 在高方差的时候使用 - 增加特征向量
 的维度,既尝试使用更多的特征 ———— 在高偏差的时候使用
的维度,既尝试使用更多的特征 ———— 在高偏差的时候使用 - 增加多项式特征,既选用更复杂假设函数
 来拟合训练集(
来拟合训练集(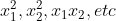 )————在高偏差的时候使用
)————在高偏差的时候使用 - 增大正则化参数
 的值 ———— 在高方差的时候使用
的值 ———— 在高方差的时候使用 - 减小正则化参数
 的值 ———— 在高偏差的时候使用
的值 ———— 在高偏差的时候使用
![J\left ( \theta \right ) = \frac{1}{2m}\left [\sum_{i = 1}^{m}\left ( h_{\theta }(x^{(i)}) -y^{(i)}\right )^{2} +\lambda \sum _{j=1}^{n}\theta _{j}^{2} \right ]](http://img.e-com-net.com/image/info8/0cf4eaa9b4bb41e886169d53aa618f42.gif)