sklearn_岭回归与多重共线性_菜菜视频学习笔记
岭回归与多重共线性
- 1.线性回归
-
- 1.1 导入需要的模块和库
- 1.2 导入数据，探索数据
- 1.3 分训练集和测试集
- 1.4 建模
- 1.5 探索建好的模型
- 2.回归类模型的评估指标
-
- 2.1 损失函数
- 2.2 成功拟合信息量占比
- 3. 多重共线性
- 4. 岭回归
-
- 4.1 岭回归解决多重共线性问题及参数Ridge
- 4.2 选取最佳的正则化参数取值
1.线性回归
1.1 导入需要的模块和库
from sklearn.linear_model import LinearRegression as LR
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.datasets import fetch_california_housing as fch #加利福尼亚房屋价值数据集,2w行，8个特征
import pandas as pd
1.2 导入数据，探索数据
housevalue = fch() #会需要下载，大家可以提前运行试试看
housevalue.data
array([[ 8.3252 , 41. , 6.98412698, ..., 2.55555556,
37.88 , -122.23 ],
[ 8.3014 , 21. , 6.23813708, ..., 2.10984183,
37.86 , -122.22 ],
[ 7.2574 , 52. , 8.28813559, ..., 2.80225989,
37.85 , -122.24 ],
...,
[ 1.7 , 17. , 5.20554273, ..., 2.3256351 ,
39.43 , -121.22 ],
[ 1.8672 , 18. , 5.32951289, ..., 2.12320917,
39.43 , -121.32 ],
[ 2.3886 , 16. , 5.25471698, ..., 2.61698113,
39.37 , -121.24 ]])
X = pd.DataFrame(housevalue.data) #放入DataFrame中便于查看
X
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 8.3252 | 41.0 | 6.984127 | 1.023810 | 322.0 | 2.555556 | 37.88 | -122.23 |
| 1 | 8.3014 | 21.0 | 6.238137 | 0.971880 | 2401.0 | 2.109842 | 37.86 | -122.22 |
| 2 | 7.2574 | 52.0 | 8.288136 | 1.073446 | 496.0 | 2.802260 | 37.85 | -122.24 |
| 3 | 5.6431 | 52.0 | 5.817352 | 1.073059 | 558.0 | 2.547945 | 37.85 | -122.25 |
| 4 | 3.8462 | 52.0 | 6.281853 | 1.081081 | 565.0 | 2.181467 | 37.85 | -122.25 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 20635 | 1.5603 | 25.0 | 5.045455 | 1.133333 | 845.0 | 2.560606 | 39.48 | -121.09 |
| 20636 | 2.5568 | 18.0 | 6.114035 | 1.315789 | 356.0 | 3.122807 | 39.49 | -121.21 |
| 20637 | 1.7000 | 17.0 | 5.205543 | 1.120092 | 1007.0 | 2.325635 | 39.43 | -121.22 |
| 20638 | 1.8672 | 18.0 | 5.329513 | 1.171920 | 741.0 | 2.123209 | 39.43 | -121.32 |
| 20639 | 2.3886 | 16.0 | 5.254717 | 1.162264 | 1387.0 | 2.616981 | 39.37 | -121.24 |
20640 rows × 8 columns
X.shape
(20640, 8)
y = housevalue.target
y
array([4.526, 3.585, 3.521, ..., 0.923, 0.847, 0.894])
y.min()
0.14999
y.max()#房价的评估，并非房价本身
5.00001
y.shape
(20640,)
X.head()
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 8.3252 | 41.0 | 6.984127 | 1.023810 | 322.0 | 2.555556 | 37.88 | -122.23 |
| 1 | 8.3014 | 21.0 | 6.238137 | 0.971880 | 2401.0 | 2.109842 | 37.86 | -122.22 |
| 2 | 7.2574 | 52.0 | 8.288136 | 1.073446 | 496.0 | 2.802260 | 37.85 | -122.24 |
| 3 | 5.6431 | 52.0 | 5.817352 | 1.073059 | 558.0 | 2.547945 | 37.85 | -122.25 |
| 4 | 3.8462 | 52.0 | 6.281853 | 1.081081 | 565.0 | 2.181467 | 37.85 | -122.25 |
housevalue.feature_names #特征名字
['MedInc',
'HouseAge',
'AveRooms',
'AveBedrms',
'Population',
'AveOccup',
'Latitude',
'Longitude']
X.columns = housevalue.feature_names
"""
MedInc：该街区住户的收入中位数
HouseAge：该街区房屋使用年代的中位数
AveRooms：该街区平均的房间数目
AveBedrms：该街区平均的卧室数目
Population：街区人口
AveOccup：平均入住率
Latitude：街区的纬度
Longitude：街区的经度
"""
'\nMedInc：该街区住户的收入中位数\nHouseAge：该街区房屋使用年代的中位数\nAveRooms：该街区平均的房间数目\nAveBedrms：该街区平均的卧室数目\nPopulation：街区人口\nAveOccup：平均入住率\nLatitude：街区的纬度\nLongitude：街区的经度\n'
1.3 分训练集和测试集
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
Xtest.head()
| MedInc | HouseAge | AveRooms | AveBedrms | Population | AveOccup | Latitude | Longitude | |
|---|---|---|---|---|---|---|---|---|
| 5156 | 1.7656 | 42.0 | 4.144703 | 1.031008 | 1581.0 | 4.085271 | 33.96 | -118.28 |
| 19714 | 1.5281 | 29.0 | 5.095890 | 1.095890 | 1137.0 | 3.115068 | 39.29 | -121.68 |
| 18471 | 4.1750 | 14.0 | 5.604699 | 1.045965 | 2823.0 | 2.883555 | 37.14 | -121.64 |
| 16156 | 3.0278 | 52.0 | 5.172932 | 1.085714 | 1663.0 | 2.500752 | 37.78 | -122.49 |
| 7028 | 4.5000 | 36.0 | 4.940447 | 0.982630 | 1306.0 | 3.240695 | 33.95 | -118.09 |
Xtrain.head()
| MedInc | HouseAge | AveRooms | AveBedrms | Population | AveOccup | Latitude | Longitude | |
|---|---|---|---|---|---|---|---|---|
| 17073 | 4.1776 | 35.0 | 4.425172 | 1.030683 | 5380.0 | 3.368817 | 37.48 | -122.19 |
| 16956 | 5.3261 | 38.0 | 6.267516 | 1.089172 | 429.0 | 2.732484 | 37.53 | -122.30 |
| 20012 | 1.9439 | 26.0 | 5.768977 | 1.141914 | 891.0 | 2.940594 | 36.02 | -119.08 |
| 13072 | 2.5000 | 22.0 | 4.916000 | 1.012000 | 733.0 | 2.932000 | 38.57 | -121.31 |
| 8457 | 3.8250 | 34.0 | 5.036765 | 1.098039 | 1134.0 | 2.779412 | 33.91 | -118.35 |
#恢复索引
for i in [Xtrain, Xtest]:
i.index = range(i.shape[0])#每行的索引等于第几行
Xtrain.shape
(14448, 8)
#如果希望进行数据标准化，还记得应该怎么做吗？
#先用训练集训练(fit)标准化的类，然后用训练好的类分别转化(transform)训练集和测试集
1.4 建模
# 建模
reg = LR().fit(Xtrain, Ytrain)
yhat = reg.predict(Xtest) #预测我们的yhat
yhat
array([1.51384887, 0.46566247, 2.2567733 , ..., 2.11885803, 1.76968187,
0.73219077])
yhat.min()
-0.6528439725035611
yhat.max()
7.1461982142709175
1.5 探索建好的模型
reg.coef_ #w,系数向量 coef:系数
array([ 4.37358931e-01, 1.02112683e-02, -1.07807216e-01, 6.26433828e-01,
5.21612535e-07, -3.34850965e-03, -4.13095938e-01, -4.26210954e-01])
Xtrain.columns
Index(['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup',
'Latitude', 'Longitude'],
dtype='object')
[*zip(Xtrain.columns,reg.coef_)] #可以解释特征重要性
[('MedInc', 0.4373589305968407),
('HouseAge', 0.010211268294494147),
('AveRooms', -0.10780721617317636),
('AveBedrms', 0.6264338275363747),
('Population', 5.21612535296645e-07),
('AveOccup', -0.0033485096463334923),
('Latitude', -0.4130959378947715),
('Longitude', -0.4262109536208473)]
"""
MedInc：该街区住户的收入中位数
HouseAge：该街区房屋使用年代的中位数
AveRooms：该街区平均的房间数目
AveBedrms：该街区平均的卧室数目
Population：街区人口
AveOccup：平均入住率
Latitude：街区的纬度
Longitude：街区的经度
"""
'\nMedInc：该街区住户的收入中位数\nHouseAge：该街区房屋使用年代的中位数\nAveRooms：该街区平均的房间数目\nAveBedrms：该街区平均的卧室数目\nPopulation：街区人口\nAveOccup：平均入住率\nLatitude：街区的纬度\nLongitude：街区的经度\n'
reg.intercept_ #intercept截距
-36.25689322920389
2.回归类模型的评估指标
2.1 损失函数
# 回归类模型的评估指标
# RSS预测值与真实值差异的和，可作为损失函数
#样本均方误差MSE(mean squared error)预测值与真实值的平均差异
from sklearn.metrics import mean_squared_error as MSE
MSE(yhat,Ytest)
0.5309012639324565
Ytest.mean()
2.0819292877906976
y.max()
5.00001
y.min()
0.14999
cross_val_score(reg,X,y,cv=10,scoring="mean_squared_error") # 交叉验证
---------------------------------------------------------------------------
KeyError Traceback (most recent call last)
File D:\py1.1\lib\site-packages\sklearn\metrics\_scorer.py:415, in get_scorer(scoring)
414 try:
--> 415 scorer = copy.deepcopy(_SCORERS[scoring])
416 except KeyError:
KeyError: 'mean_squared_error'
During handling of the above exception, another exception occurred:
ValueError Traceback (most recent call last)
Input In [36], in ()
----> 1 cross_val_score(reg,X,y,cv=10,scoring="mean_squared_error")
File D:\py1.1\lib\site-packages\sklearn\model_selection\_validation.py:513, in cross_val_score(estimator, X, y, groups, scoring, cv, n_jobs, verbose, fit_params, pre_dispatch, error_score)
395 """Evaluate a score by cross-validation.
396
397 Read more in the :ref:`User Guide `.
(...)
510 [0.3315057 0.08022103 0.03531816]
511 """
512 # To ensure multimetric format is not supported
--> 513 scorer = check_scoring(estimator, scoring=scoring)
515 cv_results = cross_validate(
516 estimator=estimator,
517 X=X,
(...)
526 error_score=error_score,
527 )
528 return cv_results["test_score"]
File D:\py1.1\lib\site-packages\sklearn\metrics\_scorer.py:464, in check_scoring(estimator, scoring, allow_none)
459 raise TypeError(
460 "estimator should be an estimator implementing 'fit' method, %r was passed"
461 % estimator
462 )
463 if isinstance(scoring, str):
--> 464 return get_scorer(scoring)
465 elif callable(scoring):
466 # Heuristic to ensure user has not passed a metric
467 module = getattr(scoring, "__module__", None)
File D:\py1.1\lib\site-packages\sklearn\metrics\_scorer.py:417, in get_scorer(scoring)
415 scorer = copy.deepcopy(_SCORERS[scoring])
416 except KeyError:
--> 417 raise ValueError(
418 "%r is not a valid scoring value. "
419 "Use sklearn.metrics.get_scorer_names() "
420 "to get valid options." % scoring
421 )
422 else:
423 scorer = scoring
ValueError: 'mean_squared_error' is not a valid scoring value. Use sklearn.metrics.get_scorer_names() to get valid options.
| # options 选项
#为什么报错了？来试试看！
import sklearn
sorted(sklearn.metrics.SCORERS.keys())
['accuracy',
'adjusted_mutual_info_score',
'adjusted_rand_score',
'average_precision',
'balanced_accuracy',
'completeness_score',
'explained_variance',
'f1',
'f1_macro',
'f1_micro',
'f1_samples',
'f1_weighted',
'fowlkes_mallows_score',
'homogeneity_score',
'jaccard',
'jaccard_macro',
'jaccard_micro',
'jaccard_samples',
'jaccard_weighted',
'matthews_corrcoef',
'max_error',
'mutual_info_score',
'neg_brier_score',
'neg_log_loss',
'neg_mean_absolute_error',
'neg_mean_absolute_percentage_error',
'neg_mean_gamma_deviance',
'neg_mean_poisson_deviance',
'neg_mean_squared_error',
'neg_mean_squared_log_error',
'neg_median_absolute_error',
'neg_root_mean_squared_error',
'normalized_mutual_info_score',
'precision',
'precision_macro',
'precision_micro',
'precision_samples',
'precision_weighted',
'r2',
'rand_score',
'recall',
'recall_macro',
'recall_micro',
'recall_samples',
'recall_weighted',
'roc_auc',
'roc_auc_ovo',
'roc_auc_ovo_weighted',
'roc_auc_ovr',
'roc_auc_ovr_weighted',
'top_k_accuracy',
'v_measure_score']
cross_val_score(reg,X,y,cv=10,scoring="neg_mean_squared_error") #负的均方误差
# 为什么使用负的均方误差？
# 因为在sklearn中损失都用负数表示，均方误差是一种误差，被认定为损失，所以使用负的均方误差。
# 在交叉验证必须使用负的均方误差
# 出来MSE我们还有MAE，绝对均值误差
array([-0.48922052, -0.43335865, -0.8864377 , -0.39091641, -0.7479731 ,
-0.52980278, -0.28798456, -0.77326441, -0.64305557, -0.3275106 ])
cross_val_score(reg,X,y,cv=10,scoring="neg_mean_squared_error").mean()
-0.5509524296956585
2.2 成功拟合信息量占比
#调用R2
#R^2=1-（真实值与预测值的差值方差和）/（真实值与均值的方差和）
# R^2所衡量的就是 1-模型没有捕捉到的信息量 占 真实标签所占的信息量 的比值
# 所以R^2越接近1 越好
from sklearn.metrics import r2_score
r2_score(yhat,Ytest) # shit tab 查看参数，线性回归模型的函数中是真实值在前还是预测值在前
0.3380653761556045
r2 = reg.score(Xtest,Ytest) #给Xtest(特征测试集)，自动生成yhat(y的标签预测值)与ytest(测试集标签)做比较
r2
0.6043668160178821
r2_score(Ytest,yhat)
0.6043668160178821
#或者你也可以指定参数，就不必在意顺序了
r2_score(y_true = Ytest,y_pred = yhat)
0.6043668160178821
cross_val_score(reg,X,y,cv=10,scoring="r2")
array([0.48254494, 0.61416063, 0.42274892, 0.48178521, 0.55705986,
0.5412919 , 0.47496038, 0.45844938, 0.48177943, 0.59528796])
cross_val_score(reg,X,y,cv=10,scoring="r2").mean()
0.5110068610524557
# 没有拟合出多少信息，40%信息遗漏
import matplotlib.pyplot as plt
sorted(Ytest)
[0.14999,
0.14999,
0.225,
0.325,
0.35,
0.375,
0.388,
0.392,
0.394,
0.396,
0.4,
0.404,
0.409,
0.41,
0.43,
0.435,
0.437,
0.439,
0.44,
0.44,
0.444,
0.446,
0.45,
0.45,
0.45,
0.45,
0.455,
0.455,
0.455,
0.456,
0.462,
0.463,
0.471,
0.475,
0.478,
0.478,
0.481,
0.481,
0.483,
0.483,
0.485,
0.485,
0.488,
0.489,
0.49,
0.492,
0.494,
0.494,
0.494,
0.495,
0.496,
0.5,
0.5,
0.504,
0.505,
0.506,
0.506,
0.508,
0.508,
0.51,
0.516,
0.519,
0.52,
0.521,
0.523,
0.523,
0.525,
0.525,
0.525,
0.525,
0.525,
0.527,
0.527,
0.528,
0.529,
0.53,
0.531,
0.532,
0.534,
0.535,
0.535,
0.535,
0.538,
0.538,
0.539,
0.539,
0.539,
0.541,
0.541,
0.542,
0.542,
0.542,
0.543,
0.543,
0.544,
0.544,
0.546,
0.547,
0.55,
0.55,
0.55,
0.55,
0.55,
0.55,
0.55,
0.55,
0.551,
0.553,
0.553,
0.553,
0.554,
0.554,
0.554,
0.555,
0.556,
0.556,
0.557,
0.558,
0.558,
0.559,
0.559,
0.559,
0.559,
0.56,
0.56,
0.562,
0.566,
0.567,
0.567,
0.567,
0.567,
0.567,
0.568,
0.57,
0.571,
0.572,
0.574,
0.574,
0.575,
0.575,
0.575,
0.575,
0.576,
0.577,
0.577,
0.577,
0.578,
0.579,
0.579,
0.579,
0.58,
0.58,
0.58,
0.58,
0.58,
0.58,
0.581,
0.581,
0.581,
0.581,
0.582,
0.583,
0.583,
0.583,
0.583,
0.584,
0.586,
0.586,
0.587,
0.588,
0.588,
0.59,
0.59,
0.59,
0.59,
0.591,
0.591,
0.593,
0.593,
0.594,
0.594,
0.594,
0.594,
0.595,
0.596,
0.596,
0.597,
0.598,
0.598,
0.6,
0.6,
0.6,
0.602,
0.602,
0.603,
0.604,
0.604,
0.604,
0.605,
0.606,
0.606,
0.608,
0.608,
0.608,
0.609,
0.609,
0.611,
0.612,
0.612,
0.613,
0.613,
0.613,
0.614,
0.615,
0.616,
0.616,
0.616,
0.616,
0.618,
0.618,
0.618,
0.619,
0.619,
0.62,
0.62,
0.62,
0.62,
0.62,
0.62,
0.62,
0.62,
0.621,
0.621,
0.621,
0.622,
0.623,
0.625,
0.625,
0.625,
0.627,
0.627,
0.628,
0.628,
0.629,
0.63,
0.63,
0.63,
0.63,
0.631,
0.631,
0.632,
0.632,
0.633,
0.633,
0.633,
0.634,
0.634,
0.635,
0.635,
0.635,
0.635,
0.635,
0.637,
0.637,
0.637,
0.637,
0.638,
0.639,
0.643,
0.644,
0.644,
0.646,
0.646,
0.646,
0.646,
0.647,
0.647,
0.647,
0.648,
0.65,
0.65,
0.65,
0.652,
0.652,
0.654,
0.654,
0.654,
0.655,
0.656,
0.656,
0.656,
0.656,
0.657,
0.658,
0.658,
0.659,
0.659,
0.659,
0.659,
0.659,
0.66,
0.661,
0.661,
0.662,
0.662,
0.663,
0.664,
0.664,
0.664,
0.668,
0.669,
0.669,
0.67,
0.67,
0.67,
0.67,
0.67,
0.67,
0.672,
0.672,
0.672,
0.673,
0.673,
0.674,
0.675,
0.675,
0.675,
0.675,
0.675,
0.675,
0.675,
0.675,
0.675,
0.675,
0.675,
0.675,
0.675,
0.676,
0.676,
0.677,
0.678,
0.68,
0.68,
0.681,
0.682,
0.682,
0.682,
0.682,
0.683,
0.683,
0.683,
0.684,
0.684,
0.685,
0.685,
0.685,
0.685,
0.686,
0.686,
0.687,
0.688,
0.689,
0.689,
0.689,
0.69,
0.69,
0.691,
0.691,
0.692,
0.693,
0.694,
0.694,
0.694,
0.694,
0.694,
0.695,
0.695,
0.695,
0.696,
0.696,
0.697,
0.698,
0.699,
0.699,
0.7,
0.7,
0.7,
0.7,
0.7,
0.7,
0.701,
0.701,
0.701,
0.702,
0.702,
0.703,
0.704,
0.704,
0.705,
0.705,
0.706,
0.707,
0.707,
0.707,
0.708,
0.709,
0.71,
0.71,
0.71,
0.711,
0.712,
0.712,
0.713,
0.713,
0.713,
0.714,
0.715,
0.716,
0.718,
0.719,
0.72,
0.72,
0.72,
0.721,
0.722,
0.723,
0.723,
0.723,
0.723,
0.723,
0.725,
0.725,
0.727,
0.727,
0.728,
0.729,
0.729,
0.73,
0.73,
0.73,
0.73,
0.73,
0.731,
0.731,
0.731,
0.731,
0.732,
0.733,
0.733,
0.734,
0.735,
0.735,
0.737,
0.738,
0.738,
0.738,
0.74,
0.74,
0.74,
0.741,
0.741,
0.741,
0.743,
0.746,
0.746,
0.747,
0.748,
0.749,
0.75,
0.75,
0.75,
0.75,
0.75,
0.75,
0.75,
0.752,
0.752,
0.754,
0.756,
0.756,
0.757,
0.759,
0.759,
0.759,
0.76,
0.76,
0.761,
0.762,
0.762,
0.762,
0.762,
0.763,
0.764,
0.764,
0.765,
0.766,
0.768,
0.769,
0.77,
0.771,
0.771,
0.771,
0.772,
0.772,
0.773,
0.774,
0.774,
0.775,
0.777,
0.777,
0.779,
0.78,
0.78,
0.78,
0.781,
0.783,
0.783,
0.785,
0.786,
0.786,
0.786,
0.786,
0.788,
0.788,
0.788,
0.788,
0.788,
0.79,
0.79,
0.79,
0.792,
0.792,
0.792,
0.795,
0.795,
0.795,
0.797,
0.797,
0.798,
0.799,
0.8,
0.801,
0.802,
0.803,
0.804,
0.804,
0.804,
0.806,
0.806,
0.808,
0.808,
0.808,
0.809,
0.81,
0.81,
0.811,
0.813,
0.813,
0.813,
0.813,
0.813,
0.813,
0.813,
0.813,
0.813,
0.813,
0.813,
0.813,
0.813,
0.813,
0.814,
0.814,
0.816,
0.817,
0.817,
0.817,
0.821,
0.821,
0.821,
0.823,
0.823,
0.824,
0.825,
0.825,
0.825,
0.826,
0.827,
0.827,
0.828,
0.828,
0.828,
0.83,
0.83,
0.83,
0.831,
0.831,
0.831,
0.832,
0.832,
0.832,
0.833,
0.833,
0.834,
0.835,
0.835,
0.836,
0.836,
0.837,
0.838,
0.839,
0.839,
0.839,
0.839,
0.84,
0.841,
0.842,
0.842,
0.842,
0.843,
0.843,
0.844,
0.844,
0.844,
0.845,
0.845,
0.845,
0.845,
0.846,
0.846,
0.846,
0.846,
0.847,
0.847,
0.847,
0.847,
0.847,
0.847,
0.848,
0.849,
0.849,
0.85,
0.85,
0.85,
0.851,
0.851,
0.851,
0.851,
0.852,
0.853,
0.853,
0.854,
0.854,
0.854,
0.855,
0.855,
0.855,
0.855,
0.856,
0.857,
0.857,
0.857,
0.857,
0.857,
0.858,
0.859,
0.859,
0.859,
0.859,
0.859,
0.861,
0.862,
0.863,
0.863,
0.863,
0.864,
0.864,
0.864,
0.864,
0.865,
0.865,
0.865,
0.866,
0.867,
0.867,
0.868,
0.869,
0.869,
0.869,
0.869,
0.87,
0.87,
0.871,
0.871,
0.872,
0.872,
0.872,
0.873,
0.874,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.875,
0.876,
0.876,
0.877,
0.877,
0.878,
0.878,
0.878,
0.879,
0.879,
0.879,
0.88,
0.88,
0.881,
0.881,
0.882,
0.882,
0.882,
0.882,
0.883,
0.883,
0.883,
0.883,
0.883,
0.883,
0.884,
0.885,
0.885,
0.886,
0.887,
0.887,
0.887,
0.888,
0.888,
0.888,
0.889,
0.889,
0.889,
0.889,
0.889,
0.89,
0.891,
0.892,
0.892,
0.892,
0.893,
0.893,
0.894,
0.895,
0.896,
0.896,
0.897,
0.897,
0.898,
0.898,
0.899,
0.9,
0.9,
0.9,
0.901,
0.901,
0.901,
0.902,
0.903,
0.903,
0.904,
0.904,
0.904,
0.905,
0.905,
0.905,
0.905,
0.906,
0.906,
0.906,
0.906,
0.907,
0.907,
0.908,
0.911,
0.911,
0.912,
0.914,
0.915,
0.915,
0.916,
0.916,
0.917,
0.917,
0.917,
0.917,
0.918,
0.918,
0.918,
0.919,
0.919,
0.919,
0.92,
0.92,
0.922,
0.922,
0.922,
0.922,
0.922,
0.924,
0.925,
0.925,
0.925,
0.925,
0.926,
0.926,
0.926,
0.926,
0.926,
0.926,
0.926,
0.926,
0.926,
0.926,
0.927,
0.927,
0.927,
0.927,
0.928,
0.928,
0.928,
0.928,
0.928,
0.929,
0.93,
0.93,
0.931,
0.931,
0.931,
0.931,
0.931,
0.931,
0.932,
0.932,
0.932,
0.932,
0.933,
0.933,
0.933,
0.934,
0.934,
0.934,
0.934,
0.934,
0.935,
0.935,
0.935,
0.936,
0.936,
0.936,
0.936,
0.938,
0.938,
0.938,
0.938,
0.938,
0.938,
0.938,
0.938,
0.938,
0.938,
0.938,
0.939,
0.939,
0.94,
0.94,
0.942,
0.942,
0.943,
0.943,
0.944,
0.944,
0.944,
0.945,
0.945,
0.946,
0.946,
0.946,
0.946,
0.946,
0.946,
0.946,
0.947,
0.947,
0.948,
0.948,
0.948,
0.949,
0.949,
0.95,
0.95,
0.95,
0.95,
0.95,
0.951,
0.952,
0.952,
0.953,
0.953,
0.953,
0.953,
0.954,
0.955,
0.955,
0.955,
0.955,
0.955,
0.956,
0.957,
0.957,
0.957,
0.958,
0.958,
0.958,
0.958,
0.958,
0.958,
0.96,
0.96,
0.96,
0.96,
0.96,
0.96,
0.961,
0.961,
0.962,
0.962,
0.962,
0.962,
0.962,
0.962,
0.962,
0.963,
0.964,
0.964,
0.964,
0.964,
0.965,
0.965,
0.965,
0.966,
0.966,
0.966,
0.967,
0.967,
0.967,
0.968,
0.968,
0.969,
0.969,
0.969,
0.969,
0.97,
0.971,
0.972,
0.972,
0.973,
0.973,
0.973,
0.974,
0.974,
0.974,
0.974,
0.976,
0.976,
0.976,
0.976,
0.977,
0.977,
0.978,
0.978,
0.978,
0.979,
0.979,
...]
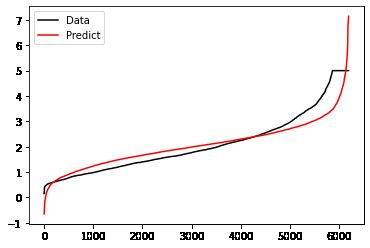
plt.plot(range(len(Ytest)),sorted(Ytest),c="black",label= "Data")
plt.plot(range(len(yhat)),sorted(yhat),c="red",label = "Predict")
plt.legend()
plt.show()
# 虽然MSE不大，但是R^2并不高，说明模型只拟合了一部份数据但是，却没有正确拟合数据的分布
# 曲线交叠的部分越多说明，模型的拟合效果越好
# 负的R^2的合理性，
# 当R^2为负数的说明我们对数据的拟合效果非常糟糕
# 这个时候就去检查建模与数据处理过程
#如果是集成回归，检查你的弱评估器数量，随机森林，提升树在只有两三棵树的时候很容易出现负的R^2
import numpy as np
rng = np.random.RandomState(42)
X = rng.randn(100, 80)
y = rng.randn(100)
X.shape
(100, 80)
y.shape
(100,)
cross_val_score(LR(), X, y, cv=5, scoring='r2')
array([-178.71468148, -5.64707178, -15.13900541, -77.74877079,
-60.3727755 ])
3. 多重共线性
# 矩阵满秩是矩阵行列式不为0的充分必要条件
# 矩阵行列式为0->矩阵的逆不存在->最小二乘法无法使用->线性回归无法求得结果
# 当矩阵中具有完全线性相关的两行，则称这两行为"精确相关关系"
#当矩阵中有两行的关系接近于"精确相关关系"，但又不是完全相关，不能使得另一行为0，这种关系被称为"高度相关关系"。、
#精确关系相关和高度相关关系并称为"多重共线性"，多重共线性下模型无法建立，或模型不可用
#总结:
# 要求线性回归的参数，矩阵的逆必须存在，矩阵的逆存在->行列式不为0->满秩->矩阵的特征之间不存在多重共线性
# 多重共线性(Multicollinearity)(精确相关关系，高度相关关系)
# 多重共线性Multicollinearity与相关性Correlation
# 相关性在机器学习中通常无伤大雅，消除相关性会减少特征，使得可用信息变得更加少，可能在排除相关性后模型的整体效果下降
# 多重共线性的存在会导致模型极大的偏移，无法模拟数据的全貌
# 改进线性回归算法来处理多重共线性
# 岭回归 Lasso 弹性网
# 岭回归 Lasso为修复多重共线性漏洞而设计的算法，在数据没有多重共线性的情况下:使用他们模型效果往往下降
# 岭回归:加正则化项(在原损失函数基础上加上一个α||w||^2)
# 正则化系数α越大，矩阵行列式变大，逆矩阵变小，以避免过大的参数向量w,so当α越大时，模型越不容易受到共线性的影响
# 当α过大时，信息占比上升会影响原数据，使得模型无法拟合数据原貌
# 所以要找到一个最佳的α来平衡共线性与模型非拟合问题
4. 岭回归
4.1 岭回归解决多重共线性问题及参数Ridge
# 如果一个数据在岭回归的各种正则化参数取值下，表现出明显的上升趋势，说明数据具有多重共线性，反之没有；
import numpy as np
import pandas as pd
from sklearn.linear_model import Ridge, LinearRegression, Lasso
from sklearn.model_selection import train_test_split as TTS
from sklearn.datasets import fetch_california_housing as fch
import matplotlib.pyplot as plt
housevalue = fch()
X = pd.DataFrame(housevalue.data)
y = housevalue.target
X.columns = ["住户收入中位数","房屋使用年代中位数","平均房间数目"
,"平均卧室数目","街区人口","平均入住率","街区的纬度","街区的经度"]
X.head()
| 住户收入中位数 | 房屋使用年代中位数 | 平均房间数目 | 平均卧室数目 | 街区人口 | 平均入住率 | 街区的纬度 | 街区的经度 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 8.3252 | 41.0 | 6.984127 | 1.023810 | 322.0 | 2.555556 | 37.88 | -122.23 |
| 1 | 8.3014 | 21.0 | 6.238137 | 0.971880 | 2401.0 | 2.109842 | 37.86 | -122.22 |
| 2 | 7.2574 | 52.0 | 8.288136 | 1.073446 | 496.0 | 2.802260 | 37.85 | -122.24 |
| 3 | 5.6431 | 52.0 | 5.817352 | 1.073059 | 558.0 | 2.547945 | 37.85 | -122.25 |
| 4 | 3.8462 | 52.0 | 6.281853 | 1.081081 | 565.0 | 2.181467 | 37.85 | -122.25 |
Xtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420)
for i in [Xtrain,Xtest]:
i.index = range(i.shape[0])
Xtrain.head()
| 住户收入中位数 | 房屋使用年代中位数 | 平均房间数目 | 平均卧室数目 | 街区人口 | 平均入住率 | 街区的纬度 | 街区的经度 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 4.1776 | 35.0 | 4.425172 | 1.030683 | 5380.0 | 3.368817 | 37.48 | -122.19 |
| 1 | 5.3261 | 38.0 | 6.267516 | 1.089172 | 429.0 | 2.732484 | 37.53 | -122.30 |
| 2 | 1.9439 | 26.0 | 5.768977 | 1.141914 | 891.0 | 2.940594 | 36.02 | -119.08 |
| 3 | 2.5000 | 22.0 | 4.916000 | 1.012000 | 733.0 | 2.932000 | 38.57 | -121.31 |
| 4 | 3.8250 | 34.0 | 5.036765 | 1.098039 | 1134.0 | 2.779412 | 33.91 | -118.35 |
#使用岭回归来进行建模
reg = Ridge(alpha=1).fit(Xtrain,Ytrain)
reg.score(Xtest,Ytest) #加利佛尼亚房屋价值数据集中应该不是共线性问题
0.6043610352312286
#交叉验证下，与线性回归相比，岭回归的结果如何变化？
alpharange = np.arange(1,1001,100)
ridge, lr = [], []
for alpha in alpharange:
reg = Ridge(alpha=alpha)
linear = LinearRegression()
regs = cross_val_score(reg,X,y,cv=5,scoring = "r2").mean()
linears = cross_val_score(linear,X,y,cv=5,scoring = "r2").mean()
ridge.append(regs)
lr.append(linears)
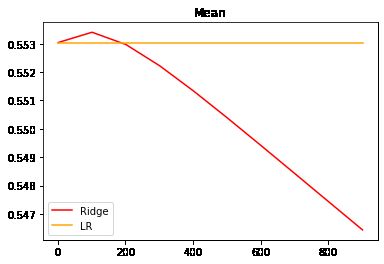
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Mean")
plt.legend()
plt.show()
#使用岭回归来进行建模
reg = Ridge(alpha=101).fit(Xtrain,Ytrain)
reg.score(Xtest,Ytest) #加利佛尼亚房屋价值数据集中的共线性应该不是什么问题
0.6035230850669475
#细化一下学习曲线
alpharange = np.arange(1,201,10)
ridge, lr = [], []
for alpha in alpharange:
reg = Ridge(alpha=alpha)
linear = LinearRegression()
regs = cross_val_score(reg,X,y,cv=5,scoring = "r2").mean()
linears = cross_val_score(linear,X,y,cv=5,scoring = "r2").mean()
ridge.append(regs)
lr.append(linears)
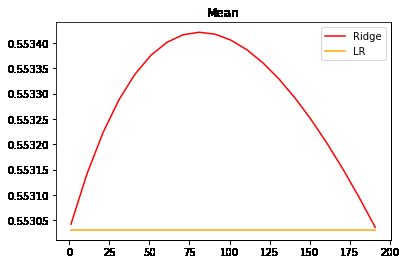
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Mean")
plt.legend()
plt.show()
#模型方差如何变化？
alpharange = np.arange(1,1001,100)
ridge, lr = [], []
for alpha in alpharange:
reg = Ridge(alpha=alpha)
linear = LinearRegression()
varR = cross_val_score(reg,X,y,cv=5,scoring="r2").var()
varLR = cross_val_score(linear,X,y,cv=5,scoring="r2").var()
ridge.append(varR)
lr.append(varLR)
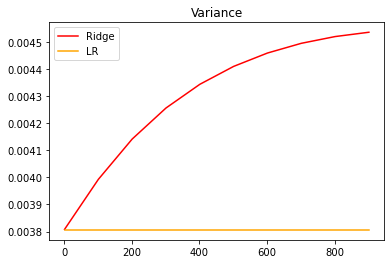
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Variance")
plt.legend()
plt.show()
# 模型的方差逐渐增大
# 泛化误差等于偏差+方差+噪声
# r^2上升接近1==模型捕捉到的信息越多==偏差下降(R^2也并不能完美表达偏差)，模型的泛化能力可能下降
#虽然R^2均值增加了，方差有些许的上升（相比R^2来说没有多少提升），因此认定泛化误差是下降的
# 还有两种影响结果的情况，
# 1.测试集并不能代表数据的全局 2.噪声的影响
# 综上所述，大多数情况下，只要r^2有比较好的增加，方差增加不多或有所减少，那么模型的泛化能力是有所增加的
from sklearn.datasets import load_boston
from sklearn.model_selection import cross_val_score
X = load_boston().data
y = load_boston().target
Xtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420)
X.shape
(506, 13)
#先查看方差的变化
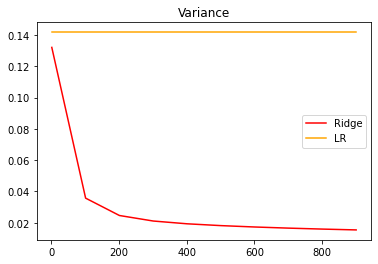
alpharange = np.arange(1,1001,100)
ridge, lr = [], []
for alpha in alpharange:
reg = Ridge(alpha=alpha)
linear = LinearRegression()
varR = cross_val_score(reg,X,y,cv=5,scoring="r2").var()
varLR = cross_val_score(linear,X,y,cv=5,scoring="r2").var()
ridge.append(varR)
lr.append(varLR)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Variance")
plt.legend()
plt.show()
# 期待目标是方差降低
#查看R2的变化
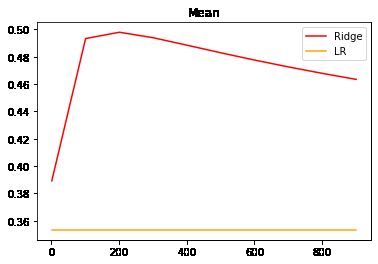
alpharange = np.arange(1,1001,100)
ridge, lr = [], []
for alpha in alpharange:
reg = Ridge(alpha=alpha)
linear = LinearRegression()
regs = cross_val_score(reg,X,y,cv=5,scoring = "r2").mean()
linears = cross_val_score(linear,X,y,cv=5,scoring = "r2").mean()
ridge.append(regs)
lr.append(linears)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Mean")
plt.legend()
plt.show()
# R^2上升，偏差降低
# 不能让R^2急速提升
#细化学习曲线
alpharange = np.arange(100,300,10)
ridge, lr = [], []
for alpha in alpharange:
reg = Ridge(alpha=alpha)
#linear = LinearRegression()
regs = cross_val_score(reg,X,y,cv=5,scoring = "r2").mean()
#linears = cross_val_score(linear,X,y,cv=5,scoring = "r2").mean()
ridge.append(regs)
lr.append(linears)
plt.plot(alpharange,ridge,color="red",label="Ridge")
#plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Mean") #得分均值
plt.legend()
plt.show()
4.2 选取最佳的正则化参数取值
# 岭迹图，alpha为横坐标，各个w的值为纵坐标
# w线条的交点越多说明，特征之间的多重共线性越高
# 所以尽量选择系数较为平稳的w曲线处对应的alpha值
# RidgeCV
# alphas 需要测试的正则化参数取值的元组
# cv默认使用留一交叉验证，只有使用留一交叉验证，才能保留交叉验证的结果
# store_cv_values 是否保存交叉验证的结果
# scoring 用来交叉验证的模型评估指标,默认R^2
# alpha_ 查看alpha
# cv_values_ 查看所有交叉验证的结果，(在每一个样本，alpha所对应的结果)
# 可使用score查看非交叉验证的得分进行对比
import numpy as np
import pandas as pd
from sklearn.linear_model import RidgeCV, LinearRegression
from sklearn.model_selection import train_test_split as TTS
from sklearn.datasets import fetch_california_housing as fch
import matplotlib.pyplot as plt
housevalue = fch()
X = pd.DataFrame(housevalue.data)
y = housevalue.target
X.columns = ["住户收入中位数","房屋使用年代中位数","平均房间数目"
,"平均卧室数目","街区人口","平均入住率","街区的纬度","街区的经度"]
Ridge_ = RidgeCV(alphas=np.arange(1,1001,100)
#,scoring="neg_mean_squared_error"
,store_cv_values=True
#,cv=5
).fit(X, y)
# 交叉验证导入全数据集不需要在分训练集和测试集
# 当设置cv=某个定值时，store_cv_values的取值必取false,
# RidgeCV不再保存交叉验证的详细结果，但任会依据评估指标最低值选择目标参数
#无关交叉验证的岭回归结果
Ridge_.score(X,y)
0.6060251767338389
#调用所有交叉验证的结果
Ridge_.cv_values_
array([[0.1557472 , 0.16301246, 0.16892723, ..., 0.18881663, 0.19182353,
0.19466385],
[0.15334566, 0.13922075, 0.12849014, ..., 0.09744906, 0.09344092,
0.08981868],
[0.02429857, 0.03043271, 0.03543001, ..., 0.04971514, 0.05126165,
0.05253834],
...,
[0.56545783, 0.5454654 , 0.52655917, ..., 0.44532597, 0.43130136,
0.41790336],
[0.27883123, 0.2692305 , 0.25944481, ..., 0.21328675, 0.20497018,
0.19698274],
[0.14313527, 0.13967826, 0.13511341, ..., 0.1078647 , 0.10251737,
0.0973334 ]])
Ridge_.cv_values_.shape
#10列对应十个不同alpha取值下的结果
#使用的是留一交叉验证所以有20640个结果
(20640, 10)
#进行平均后可以查看每个正则化系数取值下的交叉验证结果
Ridge_.cv_values_.mean(axis=0)
array([0.52823795, 0.52787439, 0.52807763, 0.52855759, 0.52917958,
0.52987689, 0.53061486, 0.53137481, 0.53214638, 0.53292369])
#查看被选择出来的最佳正则化系数
Ridge_.alpha_
101