机器学习——决策树补充
决策树补充
-
- 连续与缺失值
-
- 连续值处理
- 缺失值处理
- 代码实现
-
- 分析
- 代码获取
上一篇博客中提到了如何创建决策树，并且让决策树可视化展示，这里，我将补充连续与缺失的概念讲解，以及剪枝的代码实现。
连续与缺失值
连续值处理
什么是连续？
定义：在一定区间内可以任意取值的变量叫连续变量，其数值是连续不断的，相邻两个数值可作无限分割，即可取无限个数值。——百度百科
由定义可知，连续值得取值是无限的，不在是离散数值的有限，故不能直接根据连续属性的可取值来对结点进行划分，因此有了连续属性离散化技术。最简单的策略是采用C4.5决策树采用的机制，通过二分法对连续值进行处理
给定样本集D和连续属性a，假定a再D上出现了n个不同取值，将这些值从小到大排列，记为
。基于划分点t，可将D分为子集
和
，其中
T a = a i + a i + 1 2 ∣ 1 ≤ i ≤ n − 1 T_{a} =\frac{a^i + a^{i+1}}{2} | 1\le{i}\le{n-1} Ta=2ai+ai+1∣1≤i≤n−1
采用离散属性值方法，计算这些划分点的信息增益，选取最优的划分点进行样本集合的划分：G a i n ( D , a ) = max t ∈ T a G a i n ( D , a , t ) = max t ∈ T a E n t ( D ) − ∑ λ ∈ ( − , + ) ∣ D t λ ∣ ∣ D ∣ E n t ( D t λ ) Gain(D,a) = \max_{t\in T_a}Gain(D,a,t) = \max_{t\in T_a}Ent(D) - \sum_{\lambda \in{(-,+)}}\frac{|D_{t}^{\lambda } |}{|D|}Ent(D_{t}^{\lambda }) Gain(D,a)=t∈TamaxGain(D,a,t)=t∈TamaxEnt(D)−λ∈(−,+)∑∣D∣∣Dtλ∣Ent(Dtλ)
缺失值处理
现实中，我们的数据集样本常会遇到不完整的样本（某个特征的值为空），称为样本的某些属性值缺失。在这种情况无论是手动再次检测进行标注、还是放弃这些数据集都不太好，手动补全将会导致大量的时间浪费，而放弃将造成数据信息的巨大浪费。
西瓜书重提出了 处理缺失值需要解决两个问题：
- 如何在属性值缺失的情况下进行划分属性选择？
- 给定划分属性，若样本在该属性上的值缺失，如何对样本进行划分？
解决：
针对问题1：
给定训练集D和属性a,令
表示D中在属性a上没有缺失值的样本子集。可根据
}，令
表示
的样本子集，
表示中属于第k类（k=1,2,…,|y|)的样本子集。则有
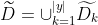
假定我们为每个样本x赋予一个权重，并定义
其中，
表示无缺失值样本所占的比例，
表示无缺失值样本中第k类所占的比例,
表示无缺失值样本中在属性a上取值
的样本所占的比例。
基于上述定义，将信息增益的计算式推广为：
其中，
针对问题二：
若样本x在划分属性a上的取值已知，则将x划入其取值对应的子节点，且样本权值在子节点中保持为
。若样本x在划分属性a上的取值未知，则将x同时划入所有子节点，且样本权值在属性值
；直观地看，这就是让同一样本以不同的概率划入到不同的子节点中去。
代码实现
关于剪枝的定义与概念，在我的上一篇文章中已有说明，这里便不在赘述点击跳转。
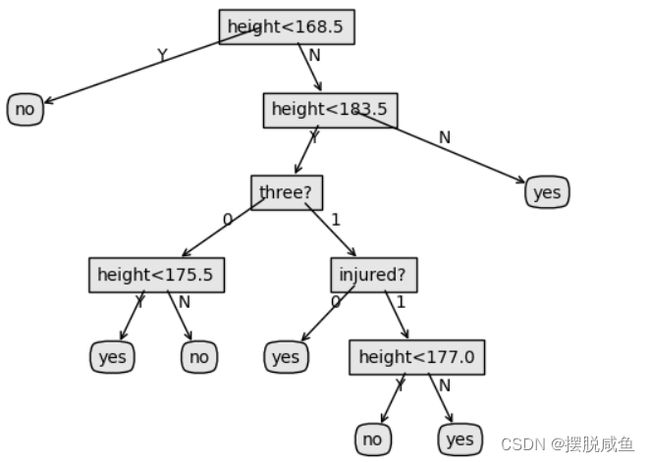
这里我通过判断集美大学国旗护卫队身高、队龄、是否受伤三个特征来判断是否能够参加10月1日的升旗队（数据是虚拟的）。
数据展示：
主要代码（以“后剪枝”为例）展示：
# 剪枝策略
def postPruningTree(inputTree, dataSet, data_test, labels, labelProperties):
firstStr = list(inputTree.keys())[0]
secondDict = inputTree[firstStr]
classList = [example[-1] for example in dataSet]
featkey = copy.deepcopy(firstStr)
if '<' in firstStr: # 对连续的特征值，使用正则表达式获得特征标签和value
featkey = re.compile("(.+<)").search(firstStr).group()[:-1]
featvalue = float(re.compile("(<.+)").search(firstStr).group()[1:])
labelIndex = labels.index(featkey)
temp_labels = copy.deepcopy(labels)
temp_labelProperties = copy.deepcopy(labelProperties)
if labelProperties[labelIndex] == 0: # 离散特征
del (labels[labelIndex])
del (labelProperties[labelIndex])
for key in secondDict.keys(): # 对每个分支
if type(secondDict[key]).__name__ == 'dict': # 如果不是叶子节点
if temp_labelProperties[labelIndex] == 0: # 离散的
subDataSet = splitDataSet_c(dataSet, labelIndex, key)
subDataTest = splitDataSet_c(data_test, labelIndex, key)
else:
if key == 'Y':
subDataSet = splitDataSet_c(dataSet, labelIndex, featvalue,
'L')
subDataTest = splitDataSet_c(data_test, labelIndex,
featvalue, 'L')
else:
subDataSet = splitDataSet_c(dataSet, labelIndex, featvalue,
'R')
subDataTest = splitDataSet_c(data_test, labelIndex,
featvalue, 'R')
if len(subDataTest) > 0:
inputTree[firstStr][key] = postPruningTree(secondDict[key],
subDataSet, subDataTest,
copy.deepcopy(labels),
copy.deepcopy(
labelProperties))
print(testing(inputTree, data_test, temp_labels,
temp_labelProperties))
print(testingMajor(majorityCnt(classList), data_test))
if testing(inputTree, data_test, temp_labels,
temp_labelProperties) <= testingMajor(majorityCnt(classList),
data_test):
return inputTree
return majorityCnt(classList)
# 测试决策树正确率
def testing(myTree, data_test, labels, labelProperties):
error = 0.0
for i in range(len(data_test)):
classLabelSet = classify(myTree, labels, labelProperties, data_test[i])
maxWeight = 0.0
classLabel = ''
for item in classLabelSet.items():
if item[1] > maxWeight:
classLabel = item[0]
if classLabel != data_test[i][-1]:
error += 1
return float(error)
# 测试投票节点正确率
def testingMajor(major, data_test):
error = 0.0
for i in range(len(data_test)):
if major[0] != data_test[i][-1]:
error += 1
return float(error)
# 测试算法
def classify(inputTree,featLabels, featLabelProperties, testVec):
firstStr = list(inputTree.keys())[0] # 根节点
firstLabel = firstStr
lessIndex = str(firstStr).find('<')
if lessIndex > -1: # 如果是连续型的特征
firstLabel = str(firstStr)[:lessIndex]
secondDict = inputTree[firstStr]
featIndex = featLabels.index(firstLabel) # 跟节点对应的特征
classLabel = {}
for key in secondDict.keys(): # 对每个分支循环
if featLabelProperties[featIndex] == 0: # 离散的特征
if testVec[featIndex] == key: # 测试样本进入某个分支
if type(secondDict[key]).__name__ == 'dict': # 该分支不是叶子节点，递归
classLabelSub = classify(secondDict[key], featLabels,
featLabelProperties, testVec)
for classKey in classLabel.keys():
classLabel[classKey] += classLabelSub[classKey]
else: # 如果是叶子， 返回结果
for classKey in classLabel.keys():
if classKey == secondDict[key][0]:
classLabel[classKey] += secondDict[key][1]
else:
classLabel[classKey] += secondDict[key][2]
elif testVec[featIndex] == 'N': # 如果测试样本的属性值缺失，则进入每个分支
if type(secondDict[key]).__name__ == 'dict': # 该分支不是叶子节点，递归
classLabelSub = classify(secondDict[key], featLabels,
featLabelProperties, testVec)
for classKey in classLabel.keys():
classLabel[classKey] += classLabelSub[key]
else: # 如果是叶子， 返回结果
for classKey in classLabel.keys():
if classKey == secondDict[key][0]:
classLabel[classKey] += secondDict[key][1]
else:
classLabel[classKey] += secondDict[key][2]
else:
partValue = float(str(firstStr)[lessIndex + 1:])
if testVec[featIndex] == 'N': # 如果测试样本的属性值缺失，则对每个分支的结果加和
# 进入左子树
if type(secondDict[key]).__name__ == 'dict': # 该分支不是叶子节点，递归
classLabelSub = classify(secondDict[key], featLabels,
featLabelProperties, testVec)
for classKey in classLabel.keys():
classLabel[classKey] += classLabelSub[classKey]
else: # 如果是叶子， 返回结果
for classKey in classLabel.keys():
if classKey == secondDict[key][0]:
classLabel[classKey] += secondDict[key][1]
else:
classLabel[classKey] += secondDict[key][2]
elif float(testVec[featIndex]) <= partValue and key == 'Y': # 进入左子树
if type(secondDict['Y']).__name__ == 'dict': # 该分支不是叶子节点，递归
classLabelSub = classify(secondDict['Y'], featLabels,
featLabelProperties, testVec)
for classKey in classLabel.keys():
classLabel[classKey] += classLabelSub[classKey]
else: # 如果是叶子， 返回结果
for classKey in classLabel.keys():
if classKey == secondDict[key][0]:
classLabel[classKey] += secondDict['Y'][1]
else:
classLabel[classKey] += secondDict['Y'][2]
elif float(testVec[featIndex]) > partValue and key == 'N':
if type(secondDict['N']).__name__ == 'dict': # 该分支不是叶子节点，递归
classLabelSub = classify(secondDict['N'], featLabels,
featLabelProperties, testVec)
for classKey in classLabel.keys():
classLabel[classKey] += classLabelSub[classKey]
else: # 如果是叶子， 返回结果
for classKey in classLabel.keys():
if classKey == secondDict[key][0]:
classLabel[classKey] += secondDict['N'][1]
else:
classLabel[classKey] += secondDict['N'][2]
return classLabel
运行结果：
通过剪枝后：
分析
相信大家看到了上述的剪枝效果后可能会发现以下问题：
- 骗人的吧，剪枝后直接通过一个特征就判断了，和自己的划分不一样啊？
- 为什么会导致这样的结果？别人的或者说教材中的都好几层。
针对上述问题：
- 数据集是我自己设计的，数据的大小和特征数量都比较少，所以说跑出来的结果效果都会比较好，大家可以去找一些数量级比较大的数据集进行测试，我相信剪纸后的结果肯定不会像我这样。
- 后剪枝的效果泛化性往往比较好，但是训练时间比较长，还和数据量的大小、特征数量有关。
剪枝的目的就是减少那些判断不明确的决策路径，使得决策路径少一点，判断的精度尽可能大一点。就像我们自己一下，当做出一次决策后，之后我们的思考可能就会变化，将一些没用的（效果不好）的判断依据去除（后剪枝）。
代码获取
链接：https://pan.baidu.com/s/1BynAi2uPx1eyZLhR6cHnww
提取码：1234