理解各种 Normalization

引言

Batch Normalization（BN）似乎已经成为构建网络不可缺少的一部分，它是如此“熟悉”以至于我天天使用却不明白原理。对此，本文梳理了 BN 的意义，实现以及一系列变体：Layer Norm，Instance Norm 和 Group Norm，这些变体和 BN 的唯一区别是均值和方差的统计范围不同。

---

Batch Normalization：2015

为了解决什么问题？

在 BN 出现之前，为了稳定地训练深度网络，需要小心地初始化网络参数，使用较低的学习率，来避免由于 saturating nonlinearities 引起的梯度消失等问题 ，这大大降低了网络的训练效率。作者认为，训练不稳定的原因是网络每一层输入的分布随着网络更新不断发生改变，网络需要不断去学习新的分布，存在 internal covariate shift。通过 BN，使每一层的输入大致满足均值为0，方差为1，从而加速训练，可以使用更大的学习率，不需要过分关注网络初始化，并且可以在一定程度上舍弃 dropout。

实现原理

一种直观的解决方法是对网络每一层的输入进行标准化，假设 $x$ 是某一层的输入，$\mathcal{X}$ 是训练集在这一层输入的集合，那么 norm 操作可以表示为：
$$\hat{x}=Norm(x,\mathcal{X})$$
这种 norm 方式十分昂贵，因为它需要在整个训练集上统计协方差矩阵 $Cov[x]=E_{x\in \mathcal{X}}[x{x}^T]-E[x]E[x{]}^T$，因此，希望找到一种简化方法，不需要在整个训练集上统计，并且可导。对此，作者增加了两种优化：

1. 独立 norm 输入的每一维而不是联合 norm 整个输入，且统计范围改为 mini-batch

假如某一层的输入有 d 维 $x=(x^1,x^2,...,x^d)$，将独立 norm 每一维，且此时均值和方差的统计范围是本次的 batch，用 batch 上的统计结果近似整个训练集的统计结果，因此使用 BN 时，一般把 batch size 设置的大一些，当 batch size = 1 时，相当于没有使用 BN。
$${\hat{x}}^k=\frac{x^k-E[x^k]}{\sqrt{Var[x^k]}}$$

2. 引入参数 ${\gamma }^k,{\beta }^k$

仅仅 norm 输入可能会改变网络层的表达，例如，对 sigmoid 的输入进行 norm 会将非线性限制在线性区域，为了解决这个问题，作者认为 norm 层应该也能表达 identity function，因此，针对每个 ${\hat{x}}^k$，还引入一对参数 ${\gamma }^k,{\beta }^k$：
$$y^k={\gamma }^k{\hat{x}}^k+{\beta }^k$$
BN算法流程如下，经计算 BN 是可导的[1]：
$$\begin{array}{rl}& \mathbf{Input}:\text{Values of }x\text{ over a mini-batch }\mathcal{B}=\{x_{\mathrm{1...}m}\};\\ & \text{Parameters to be learned }\gamma ,\beta \\ & \mathbf{Output}:\{y_i=B{N}_{\gamma ,\beta }(x_i)\}\\ & {\mu }_{\mathcal{B}}=\frac{1}{m}\sum _{i=1}^m{x}_i\\ & {\sigma }_{\mathcal{B}}^2=\frac{1}{m}\sum _{i=1}^m(x_i-{\mu }_{\mathcal{B}}{)}^2\\ & {\hat{x}}_i=\frac{x_i-{\mu }_{\mathcal{B}}}{\sqrt{{\sigma }_{\mathcal{B}}^2+ϵ}}\\ & y_i=\gamma {\hat{x}}_i+\beta \equiv B{N}_{\gamma ,\beta }(x_i)\end{array}$$
其中 $ϵ$ 是为了稳定计算引入的常数。

推理过程

推理过程中，每一层学习到的 ${\gamma }^k,{\beta }^k$ 固定，且每一层的 $E[x],Var[x]$ 不再是 batch 上的统计结果，而是训练集上的统计结果，因此推理过程中的 BN 是一个线性映射。训练中会记录每一个 batch 的 ${\mu }_{\mathcal{B}},{\sigma }_{\mathcal{B}}^2$，推理时利用它们的移动平均近似训练集上的 $E[x],Var[x]$：
$$\begin{array}{rl}E[x]& \leftarrow E_{\mathcal{B}}[{\mu }_{\mathcal{B}}]\\ Var[x]& \leftarrow \frac{m}{m-1}{E}_{\mathcal{B}}[{\sigma }_{\mathcal{B}}^2]\\ y& =\frac{\gamma }{\sqrt{Var[x]+ϵ}}\cdot x+(\beta -\frac{\gamma E[x]}{\sqrt{Var[x]+ϵ}})\end{array}$$

Layer Normalization：2016

Layer Normalization（LN）认为 BN 不好应用到 RNN 上，且当 batch size = 1 时 BN 也无法使用（在 RNN 中，当序列很长时，由于存储容量的限制使 batch size 不能设置的很大）。其统计范围是数据的通道，设网络某一层的输入是 $x\in {\mathbb{R}}^{B\times C\times H\times W}$，B，C，HW 分别代表数据的 batch size，通道数和空间维度，有：
$$\begin{array}{rl}{\mu }_b& =\frac{1}{C}\sum _{i=1}^C{x}_i\\ {\sigma }_b^2& =\frac{1}{C}\sum _{i=1}^C(x_i-{\mu }_b{)}^2\end{array}$$

Instance Normalization：2017

IN 是研究风格迁移问题时提出的，作者认为迁移图像的对比度应该和风格图像相似，生成器应该丢弃内容图像的对比度信息，从而提出 IN 为了 norm 图像中的对比度信息。

Intuitively, the normalization process allows to remove instance-specific contrast information from the content image, which simplifies generation.

设网络某一层的输入是 $x\in {\mathbb{R}}^{B\times C\times H\times W}$，B，C，HW 分别代表数据的 batch size，通道数和空间维度，有：
$$\begin{array}{rl}{\mu }_{b,c}& =\frac{1}{HW}\sum _{i=1}^{HW}{x}_i\\ {\sigma }_{b,c}^2& =\frac{1}{HW}\sum _{i=1}^{HW}(x_i-{\mu }_{b,c}{)}^2\end{array}$$

Group Normalizaztion 2018

作者认为当 batch size 很小（例如 batch size = 2）时，BN 的性能会剧烈下降，GN 在 batch size 很小时性能比 BN 好，且在 batch size 大时两者性能相当，GN 将通道分成 groups，然后在 groups 上统计均值和方差。设网络某一层的输入是 $x\in {\mathbb{R}}^{B\times G\times H\times W}$，B，G，HW 分别代表数据的 batch size，组数和空间维度，有：
$$\begin{array}{rl}{\mu }_{b,g}& =\frac{1}{G}\sum _{i=1}^G{x}_i\\ {\sigma }_{b,g}^2& =\frac{1}{G}\sum _{i=1}^G(x_i-{\mu }_{b,g}{)}^2\end{array}$$

总结

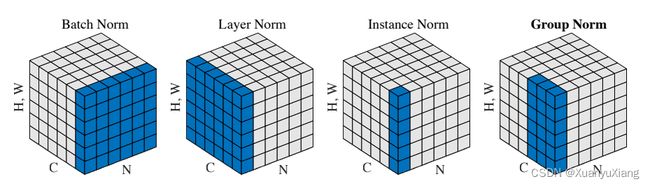
BN，LN，IN，GN 在理解 BN 的基本原理后，用一张图记忆即可：

参考

[1] Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
[2] Layer Normalization
[3] Instance Normalization: The Missing Ingredient for Fast Stylization
[4] Group Normalization