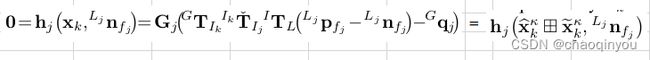论文阅读笔记： fast-lio系列

code: https://github.com/hku-mars/FAST_LIO

paper:

  fast-lio: https://arxiv.org/abs/2010.08196

  fast-lio2: FAST_LIO/Fast_LIO_2.pdf at main · hku-mars/FAST_LIO · GitHub  

====

(2020) FAST-LIO: A Fast, Robust LiDAR-inertial Odometry Package by Tightly-Coupled Iterated Kalman Filter

一、贡献

1. 一种用interated kalman filter实现的直接法紧耦合LIO, 其核心是提出的kalman gain的计算方法的复杂度只和状态的维度有关（经典的kalman filter的kalman gain的计算复杂度和观测的复杂度有关，本文的作者发现了一种等效的形式， 矩阵求逆的维度从观测数量的维度减少到状态数量的维度），从而能够在移动计算平台达到实时计算；

2. 提出了一种激光去畸变的方法（作者称为back-propagation）;

3. 代码开源，实验充分

二、性能

基于大疆的移动计算平台： DJI Manifold 2-C（i7-8550U/8G RAM）

1. 时间：

2. 无人机场景精度： 32m漂移0.08m 

3. 室外场景精度： 140m漂移0.07m

4. 室内快速旋转（>100°/s）, 定性分析，可见细节还原还是很好的：

三、实现方案

3.1 系统框图和符号定义

基本过程： 激光雷达特征提取 -> 状态估计和运动补偿 -> 残差计算和状态更新 ->  地图更新 

3.2 运动学模型 

3.3 状态转移方程

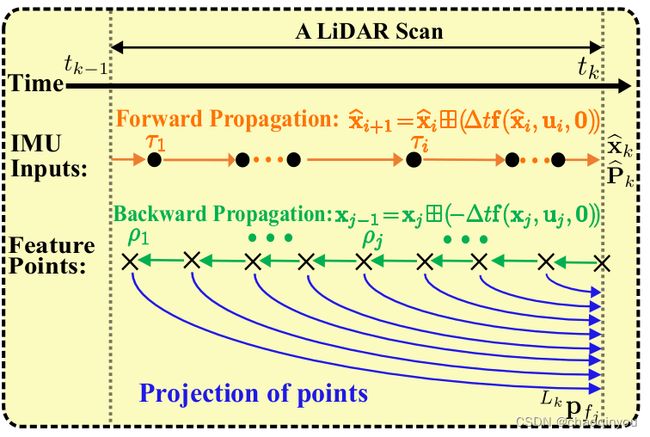
3.4 状态估计和运动补偿（forward propagation and backward propagation） 

3.4.1 状态预测：

利用k-1时刻的后验状态及其协方差， 以k-1到k期间的各个imu测量量为控制逐个“传播”， 预测k时刻的状态和协方差。

状态传播时设噪声为0, 所以各个i时刻的ba, bg和g都和k-1时刻一致；

协方差传播时噪声为常数；

3.4.2 运动补偿

激光雷达的各个点是在k-1到k时刻之间逐步获得的，需要把它们换算到k时刻后才能作为测量进行状态更新；

激光雷达的扫描频率远高于IMU， 因此处在i-1到i时刻的激光点共享i-1处的imu测量：

 得到相对位姿后，把每个点都补偿到k时刻：

3.5 残差计算

在map坐标系下面， 计算激光面特征和线特征到最近的面和线的距离（fast-lio2里面貌似只用了面特征）：

3.6 状态更新

状态目的是通过迭代，获得一个对误差量的估计，用于把之前的预测值调准；

因此可以构建如式17的目标函数，在真值距离预测值不会太大的先验条件下， 使得残差最小；

式17中对于后面残差这一项要特别说明一下:

观测函数h在（上一次迭代）的预测值固定后， 是误差状态的函数：

注意到error state一般在0附近， 因此我们可以对（关于error state的）观测函数在0附近展开，并取一阶近似：

 ， 其中H是观测函数对于error state的雅各比矩阵；

优化式17，能得到迭代的递推公式：

 其中K只和状态的维度有关， 相比经典的kalman gain的计算（） ，求逆的维度大幅降低

 总体算法如下：

3.5 建图： 用收敛后的pose，把去畸变之后的点云加到之前map中；

3.6 初始化： 开机静止放几秒钟， 让重力加速度， bg, ba和噪声协方差初始化， 加速收敛； 

四、重要参考文献

1. iterated Kalman Filter: (2019.07) LINS: A Lidar-Inertial State Estimator for Robust and Efficient Navigation

====

(2021.07) FAST-LIO2: Fast Direct LiDAR-inertial Odometry

主要贡献是ikdtre