城市空气质量分析与预测

一、AQI分析与预测

1、背景信息

AQI指的是空气质量指数，用来衡量一个城市的空气清洁或污染的程度，数值越小则空气质量越好。近年来，空气污染问题备受关注，现收集不同城市的数据，运用数据分析的方法来对不同城市的空气质量进行分析与预测。

2、任务说明

我们期望能够运用数据分析的相关技术，对全国城市的空气质量进行分析与预测，同时会根据分析结果来解决一些常见问题，例如：

• 哪些城市的空气质量比较好？哪些比较差？
• 空气质量在地理上的分布，是否存在着一定的规律？
• 沿海城市与内陆城市的空气质量是否存在不同？
• 空气质量主要受到哪些因素的影响？
• 全国空气质量的整体情况是怎样的？
• 怎么来预测一个城市的空气质量？

3、数据集描述

我们现在获取了2015年的空气质量数据集，该数据集包含的是全国主要城市的相关数据及空气质量指数，数据情况如下：

列名	含义
City	城市名
AQI	空气质量指数
Precipitation	降雨量
GDP	城市生产总值
Temperature	温度
Longitude	纬度
Latitude	经度
Altitude	海拔高度
PopulationDensity	人口密度
Coastal	是否沿海
GreenCoverageRate	绿化覆盖率
Incineration(10000ton)	焚烧量(10000吨)

二、数据分析流程

基本流程

在进行数据分析之前，我们清楚整个分析流程，每个流程所对应的步骤与使用的相关分析技术：

• 明确任务需求与分析目标
• 数据收集：
  • 内部数据、购买数据、爬取数据、调查问卷、其他收集
• 数据预处理：
  • 数据整合（横向整合、纵向整合）
  • 数据清洗（缺失值、异常值、重复值）
  • 数据转换
• 数据分析：
  • 描述性分析
  • 推断分析
  • 数据建模（特征方程、超参数调整）
  • 数据可视化
• 编写报告

三、读取数据

1、导入相关的库

导入相关的库，同时进行一些初始化的设置

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings

sns.set(style='darkgrid')
plt.rcParams['font.family']='SimHei'
plt.rcParams['axes.unicode_minus']=False
warnings.filterwarnings('ignore')

2、加载数据集

data=pd.read_csv('data.csv')
print(data.shape)
（325，12）

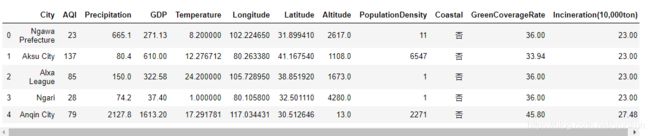
加载后，可以使用head/tail/sample等方法查看数据的大致情况：

data.head()

四、数据清洗

1、缺失值

1.1、缺失值探索

我们可以用以下方法来查看缺失值：

• info
• is null

#data.info()
data.isnull().sum(axis=0)

1.2、缺失值处理

对于缺失值，我们可以使用以下处理方式：

• 删除缺失值：仅适合于缺失值很少的情况
• 填充缺失值：
  • 数值变量：
    • 均值填充
    • 中值填充
  • 类别变量：
    • 众数填充
    • 单独作为一个类别
  • 额外处理说明：
    • 缺失值小于20%，直接填充
    • 缺失值在20%-80%，填充变量后，同时增加一列，标记该列是否缺失，参与后续建模
    • 缺失值大于80%，不用原始列，而是增加一列，标记该列是否缺失，参与后续建模

1、数据分布

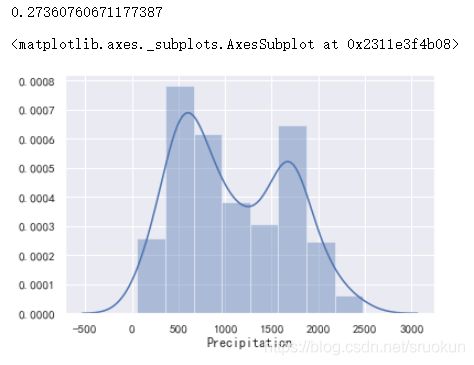
print(data['Precipitation'].skew())
sns.distplot(data['Precipitation'].dropna())

2、填充数据

data.fillna({'Precipitation':data['Precipitation'].median()},inplace=True)
data.isnull().sum()

2、异常值

2.1、异常值探索

我们可以如下方法来发现缺失值：

• describe查看数值信息
• 正态分布3个标准差外(3σ)的方式
• 使用箱线图辅助
• 相关异常检测算法

1、describe方法

调用DataFrame对象的describe方法，可以显示数据的统计信息，但仅为一种简单的异常探索方式，不够直观，局限性强。

2、3σ的方式

根据正态分布的特性，我们可以将3个标准差外（3σ）的数据，视为异常值。现在我们以GDP为例，首先先绘制GDP的分布图

sns.distplot(data['GDP'])
print(data['GDP'].skew())

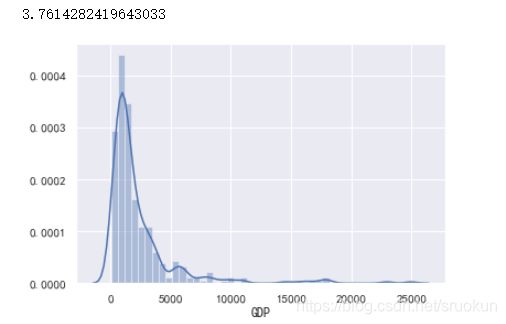
由图看出数据呈现严重右偏分布，也就是存在很多极大异常值，我们先获取这些异常值。

mean,std=data['GDP'].mean(),data['GDP'].std()
lower,upper = mean-3*std,mean+3*std

print('均值',mean)
print('标准差',std)
print('下限',lower)
print('上限',upper)
data['GDP'][(data['GDP']<lower)|(data['GDP']>upper)]

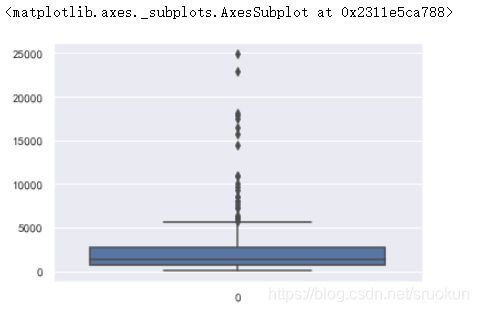
3、箱线图

箱线图也是一种常见的异常值检测方式。

sns.boxplot(data=data['GDP'])

2.2、异常值处理

对于异常值，我们可以用以下的方式来处理：

• 删除异常值
• 视为缺失值
• 对数转换
• 使用临界值填充
• 使用分箱法离散化处理

1、对数转换

如果数据中存在较大的异常值，可以通过采用对数来进行转化，能得到一定的缓解。例如GDP变量呈现右偏分布

import matplotlib.pyplot as plt
fig,ax = plt.subplots(1,2)
fig.set_size_inches(15,5)
sns.distplot(data['GDP'],ax=ax[0])
sns.distplot(np.log(data['GDP']),ax=ax[1])

取对数的方式比较简单，不过也存在着局限性，比如：

• 对数转换值针对正数操作，不过可以采用以下方式进行转换：

  *np.sign(X)np.log(np.abs(X)+1)

• 适合右偏分布，不适合左偏分布，不过现实中大多数的数据一般的呈右偏分布较多。

2、使用边界值替换

对异常值进行‘截断’处理，即使用临界值替换异常值。例如在3σ与箱线图可以这样处理

3、分箱离散化

有时候特征对目标值存在一定的影响，可能未必是线性的增加，这时可以使用分箱方式，对特征进行离散化处理。
分箱离散化分为两个阶段：

• 分箱：比如将不同年龄段的人进行分化区间，例如0-18岁、18岁-30岁、30岁-40岁、40岁以上。
• 离散化：可以将不同年龄段依次对应为1、2、3、4，作为离散化处理。最后输入模型中进行分析

3、重复值

3.1、重复值的探索

使用duplicate检查重复值，可配合keep参数进行调整

#发现重复值
print(data.duplicated().sum())
#查看哪些记录出现重复值
data[data.duplicated(keep=False)]

3.2、重复值处理

重复值对数据分析通常没有作用，直接删除即可

data.drop_duplicates(inplace=True)
data.duplicated().sum()

五、数据分析

1、空气质量最好/最差的5个城市

1.1、空气质量最好的5个城市

t=data[['City','AQI']].sort_values('AQI')
display(t.iloc[:5])
plt.xticks(rotation=45)
sns.barplot(x='City',y='AQI',data=t.iloc[:5])

1.2、空气质量最差的5个城市

display(t.iloc[:-5])
plt.xticks(rotation=45)
sns.barplot(x='City',y='AQI',data=t.iloc[-5:])

2、全国城市的空气质量

2.1、城市空气质量等级统计

对于AQI，可以对空气质量进行等级划分，划分标准如下：

AQI指数	等级	描述
0-50	一级	优
51-100	二级	良
101-150	三级	轻度污染
151-200	四级	中度污染
201-300	五级	重度污染
>300	六级	严重污染

根据该标准，我们来统计下，全国空气质量每个等级的数量。

# 编写函数，将AQI转换为对应的等级。
def value_to_level(AQI):
    if AQI>=0 and AQI<=50:
        return '一级'
    elif AQI>=51 and AQI<=100:
        return '二级'
    elif AQI>=101 and AQI<=150:
        return '三级'
    elif AQI>=151 and AQI<=200:
        return '四级'
    elif AQI>=201 and AQI<=300:
        return '五级'
    else:
        return '六级'
level = data['AQI'].apply(value_to_level)
display(level.value_counts())
sns.countplot(x=level,order=['一级','二级','三级','四级','五级'])

2.2、空气质量分布

我们来绘制下全国各城市的空气质量分布图。

sns.scatterplot(x='Longitude',y='Latitude',hue='AQI',palette=plt.cm.RdYlGn_r,data=data)

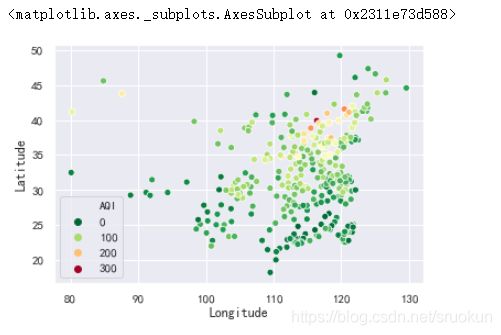
从结果上可以发现，从大致的地理位置，西部城市好于东部城市，南部城市好于北部城市。

3、临海城市是否空气质量优于内陆城市

3.1、数量统计

我们先来统计下临海城市与内陆城市的数量

display(data['Coastal'].value_counts())
sns.countplot(x='Coastal',data=data)

3.2、分布统计

然后我们来观察临海城市与内陆城市的散点分布

sns.swarmplot(x='Coastal',y='AQI',data=data)

然后我们来分组计算空气质量的均值:

display(data.groupby('Coastal')['AQI'].mean())
sns.barplot(x='Coastal',y='AQI',data=data)

在柱状图中，仅显示了内陆城市与沿海城市的空气质量指数（AQI）的均值对比，我们也可以用箱线图来显示更多的信息。(上图均值的竖线是均值的置信区间)

sns.boxplot(x='Coastal',y='AQI',data=data)

3.3、差异检验

这里，我们可以进行两样本的t检验，来查看临海城市与内陆城市的均值差异是否显著

from scipy import stats
Coastal = data[data['Coastal']=='是']['AQI']
inland = data[data['Coastal']=='否']['AQI']
#进行方差齐性检验，为后续的两样本的t检验服务。
stats.levene(Coastal,inland)

LeveneResult(statistic=0.08825036641952543, pvalue=0.7666054880248168)
这里原假设方差是相等的也就是齐性的，检验结果看P值，P值就是对原假设的支持概率，这里pvalue=0.76，则说明两独立样本是齐性的。

#进行两样本的t检验。注意。两样本的方差相同与不同，取得的结果是不同的，这里equal_var=True说明方差是相等的。
r = stats.ttest_ind(Coastal,inland,equal_var=True)
print(r)
p = stats.t.sf(r.statistic,df=len(Coastal)+len(inland)-2)
print(p)

Ttest_indResult(statistic=-2.7303827520948905, pvalue=0.006675422541012958)
0.9966622887294936
这里的P值很小则说明，原假设不成立即沿海城市与内陆城市均值不相等。同时怎么判断两个样本均值的大小，看statistic，这里是负值说明，沿海城市均值小于内陆城市均值。

4、空气质量主要受哪些因素影响

比如我们可能会关注这些问题：

• 人口密度大，是否会对空气质量造成负面影响？
• 绿化率高，是否会提高空气质量？

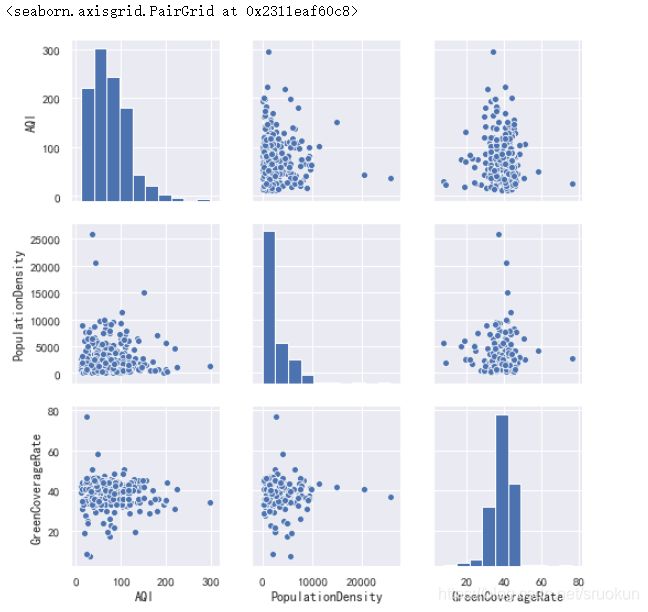
4.1、散点图矩阵

sns.pairplot(data[['AQI','PopulationDensity','GreenCoverageRate']])
#sns.pairplot(data[['AQI','PopulationDensity','GreenCoverageRate']],kind='reg')

4.2、相关系数

1、协方差定义

2、相关系数定义

我们以空气质量（AQI）与降雨量（Precipitation）为例，计算二者的相关系数：

x = data['AQI']
y = data['Precipitation']
#计算两个变量的协方差
a =(x - x.mean())*(y-y.mean())
cov = np.sum(a)/(len(a)-1)
print('协方差：',cov)
#计算两个变量的相关系数
corr = cov/np.sqrt(x.var()*y.var())
print('相关系数：',corr)

协方差： -10098.209013903044
相关系数： -0.40184407003013883

不过DataFrame对象提供了计算相关系数的方法。我们可以直接使用

data.corr()

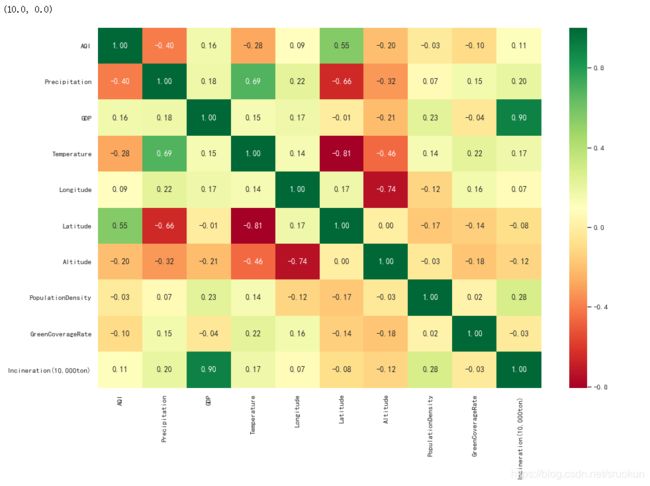
为了能够更清晰的呈现相关系数值，我们可以用热图来显示相关系数

plt.figure(figsize=(15,10))
ax = sns.heatmap(data.corr(),cmap=plt.cm.RdYlGn,annot=True,fmt='.2f')
#注意：Matplotlib3.1.1版本的bug，heatmap的首行与末行会显示不全。
#可手动调整y轴的范围来进行修复。
a,b=ax.get_ylim()
ax.set_ylim(a+0.5,b-0.5)

4.3、结果统计

从结果中可知，空气质量主要受降雨量（-0.4）与纬度（0.55）影响

• 降雨量越多，空气质量越好。
• 纬度越低，空气质越好

此外，我们还能发现其他的明显细节：

• GDP (城市生产总值) 与Incineration (焚烧量)正相关(0.90)。
• Temperature (温度)与Precipitation (降雨量)正相关(0.69)。
• Temperature (温度)与Latitude (纬度)负相关(-0.81)。
• Longitude (经度)与Altitude (海拔)负相关(-0.74)。
• Latitude (纬度)与Precipitation (降雨量)负相关(-0.66)。
• Temperature (温度)与Altitude (海拔)负相关(-0.46)。
• Altitude (海拔)与Precipitation (降雨量)负相关(-0.32)。

5、关于空气质量的消息真假验证

网上有传闻说，全国所有城市的空气质量指数均值在71左右，请问，这个消息可靠嘛？
我们可以采用假设检验来验证。
首先，城市的平均空气质量指数，我们肯容易就能进行计算。

data['AQI'].mean()

75.3343653250774

该需求是要验证样本均值是否等于总体均值，根据场景，我们可以使用单样本t检验，置信度为95%

r = stats.ttest_1samp(data['AQI'],71)
print('t值：',r.statistic)
print('p值：',r.pvalue) 

t值： 1.8117630617496872
p值： 0.07095431526986647
我们可以看到，P值大于0.05，故我们无法拒绝原假设，因此接受原假设。
我们要清楚，+ -1.96倍的标准差，是正态分布在置信区间为95%下的临界值，严格来说，对 t 分布不是如此，
只不过，当样本容量较大时，t分布近似正态分布。但当样本容量较小时，二者会有较大的差异。
我们可以获取更准确的置信区间：

mean=data['AQI'].mean()
std=data['AQI'].std()
stats.t.interval(0.95,df=len(data)-1,loc=mean,scale=std/np.sqrt(len(data)))

由此，我们就计算出全国所有城市平均空气质量指数，95%的可能大致在70.63-80.04之间。

6、对空气质量的预测

对于某城市，如果我们已知降雨量，温度，经纬度等指标。我们是否能够预测该城市的空气质量指数呢？答案是肯定的。我们可以通过对以往的数据，去建立一种模式，然后将这种模式去应用于未知的数据，进而预测结果。

6.1、数据转换

对于模型来说，内部进行的都是数学上的运算，在进行建模之前，我们需要首先进行转换，将类别变量转换为离散变量。

data['Coastal'] = data['Coastal'].map({'是':1,'否':0})
data['Coastal'].value_counts()

6.2、基模型

首先，我们不进行任何处理，建立一个模型，后续的操作，可以在此基础上进行改进。

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split

X = data.drop(['City','AQI'],axis=1)
y = data['AQI']
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0)

lr=LinearRegression()
lr.fit(X_train,y_train)
print(lr.score(X_train,y_train))
print(lr.score(X_test,y_test))

0.4538897765064036
0.40407705623835266

y_hat=lr.predict(X_test)
plt.figure(figsize=(15,5))
plt.plot(y_test.values,'-r',label='真实值',marker='o')
plt.plot(y_hat,'-g',label='测试值',marker='D')
plt.legend(loc='upper left')
plt.title('线性回归预测结果',fontsize=20)

6.3、特征选择

刚才，我们使用所有可能的原始数据作为特征，建立模型，然而，特征并非越多越好，有些特征可能对模型质量并没有什么改善，能够提高模型训练速度。

1、RFECV

特征选择方式有很多，这里我们用RFECV方法来实现特征选择。RFECV分为两个部分，分别是：

• RFE：递归特征消除，用来对特征进行重要性评级。
• CV：交叉检验，在特征评级后，通过交叉检验，选择最佳数量的特征。
  具体过程如下：
• RFE阶段：
  1、初始的特征集为所有可用的特征。
  2、使用当前特征集进行建模，然后计算每个特征的重要性。
  3、删除最不重要的一个（或多个）特征，更新特征集。
  4、跳转到步骤2，直到完成所有特征的重要性评级。
• CV阶段：
  1、根据RFE阶段确定的特征重要性，依次选择不用数量的特征。
  2、对选定的特征集进行交叉检验。
  3、确定平均分最高的特征集数量，完成特征选择。

特征选择实例

from sklearn.feature_selection import RFECV
#estimator:要操作的模型
#step:每次删除的变量数
#cv:使用的交叉检验折数
#n_jobs:并发的数量
#scoring:评估的方式
rfecv = RFECV(estimator=lr,step=1,cv=5,n_jobs=-1,scoring='r2')
rfecv.fit(X_train,y_train)
#返回经过选择之后，剩余的特征数量
print(rfecv.n_features_)
#返回经过特征选择后，使用缩减特征后的模型
print(rfecv.estimator)
#返回每个特征的等级，数值越小，特征越重要
print(rfecv.ranking_)
#返回布尔数组，用来表示特征是否被选择。
print(rfecv.support_)
#返回对应数量特征时，模型交叉检验的评分
print(rfecv.grid_scores_)

8
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
[1 2 1 1 1 1 3 1 1 1]
[ True False True True True True False True True True]
[-0.06091362 0.1397744 0.2302962 0.22814855 0.22644355 0.21342713
0.24573222 0.26368987 0.25744818 0.25389817]

通过结果可知，我们成功删除了两个特征。可以绘制下，在特征选择过程中，使用交叉检验获取的R平方值。

plt.plot(range(1,len(rfecv.grid_scores_)+1),rfecv.grid_scores_,marker='o')
plt.xlabel('特征数量')
plt.ylabel('交叉检验$R^2$值')

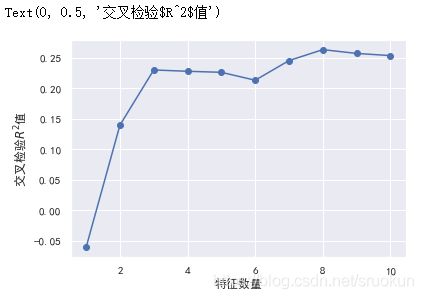
然后，我们对测试集应用这种特征选择（变换），进行测试，获取测试结果。

print('剔除的变量：',X_train.columns[~rfecv.support_])
X_train_eli = rfecv.transform(X_train)
X_test_eli = rfecv.transform(X_test)
print(rfecv.estimator_.score(X_train_eli,y_train))
print(rfecv.estimator_.score(X_test_eli,y_test))

剔除的变量： Index([‘GDP’, ‘PopulationDensity’], dtype=‘object’)
0.45322255556356406
0.39822556329575864

结论：我们发现，经过特征选择后，消除了GDP与PopulationDensity两个特征，而使用剩余8个特征训练的模型，与之前未消除特征训练的模型（使用全部10个特征训练的模型），无论在训练集还是测试集的表现上，都几乎相同，这就可以证明，我们清楚的这两个特征，确实对拟合目标（y值）没有什么帮助，可以去掉。

7、异常值的处理

如果数据中存在异常值，可能会影响模型的效果，因此，我们在建模之前，有必要对异常值进行处理

7.1、使用临界值替换

我们可以依据箱线图判断离群点的原则去探索异常值，然后使用临界值，替换掉异常值。

#Coastal是类别变量，映射为离散变量，不会有异常值
for col in X.columns.drop('Coastal'):
    if pd.api.types.is_numeric_dtype(X_train[col]):
        quartile = np.quantile(X_train[col],[0.25,0.75])
        IQR = quartile[1]-quartile[0]
        lower = quartile[0]-1.5*IQR
        upper = quartile[1]+1.5*IQR
        X_train[col][X_train[col]<lower]=lower
        X_train[col][X_train[col]>upper]=upper
        X_test[col][X_test[col]<lower]=lower
        X_test[col][X_test[col]>upper]=upper

7.2、效果对比

去除异常值后，我们使用新的训练集与测试集来评估模型的效果

lr.fit(X_train,y_train)
print(lr.score(X_train,y_train))
print(lr.score(X_test,y_test))

0.4631142291492417
0.446142026583966

效果相对之前，似乎有着轻微的改进，不过并不明显，我们可以使用RFECV在去除异常值的数据上，再次尝试

rfecv = RFECV(estimator=lr,step=1,cv=5,n_jobs=-1,scoring='r2')
rfecv.fit(X_train,y_train)
print(rfecv.n_features_)
print(rfecv.estimator_)
print(rfecv.ranking_)
print(rfecv.support_)
print(rfecv.grid_scores_)

plt.plot(range(1,len

(rfecv.grid_scores_)+1),rfecv.grid_scores_,marker='o')
plt.xlabel('特征数量')
plt.ylabel('交叉检验$R^2$值')

print('剔除的变量：',X_train.columns[~rfecv.support_])
# X_train_eli = rfecv.transform(X_train)
# X_test_eli = rfecv.transform(X_test)
X_train_eli = X_train[X_train.columns[rfecv.support_]]
X_test_eli = X_test[X_test.columns[rfecv.support_]]
print(rfecv.estimator_.score(X_train_eli,y_train))
print(rfecv.estimator_.score(X_test_eli,y_test))

剔除的变量： Index([‘PopulationDensity’], dtype=‘object’)
0.46306656191488615
0.4450225589408254

7.3、分箱操作

注意：分箱后，我们不能将每个区间映射为离散数值，而是应当使用One-Hot编码。

from sklearn.preprocessing import KBinsDiscretizer
#KBinsDiscretizer K个分箱离散器。用于将数值（通常是连续变量）变量进行区间离散化操作。
#n_bins:分箱（区间）的个数
#encode:离散化编码方式。分为：onehot,onehot-dense与ordinal
#        onehot:使用独热编码，返回稀疏矩阵
#        onehot-dense:使用独热编码，返回稠密矩阵
#        ordinal:使用序数编码（0,1,2...）
#strategy:分箱的方式。分为：uniform,quantile,kmeans。
#        uniform:每个区间长度范围大致相同
#        quantile:每个区间包含的元素大致相同
#        kmeans:使用一维kmeans方式进行分箱。
k = KBinsDiscretizer(n_bins=[4,5,14,6],encode='onehot-dense',strategy='uniform')
#定义离散化的特征。
discretize = ['Longitude','Temperature','Precipitation','Latitude']

r = k.fit_transform(X_train_eli[discretize])
r = pd.DataFrame(r,index=X_train_eli.index)
#获取离散化后特征之外的其他特征
X_train_dis = X_train_eli.drop(discretize,axis =1)
#获取离散化后的特征与其他特征进行重新组合
X_train_dis = pd.concat([X_train_dis,r],axis =1)
#对测试集进行同样的离散化操作。
r = pd.DataFrame(k.transform(X_test_eli[discretize]),index=X_test_eli.index)
X_test_dis = X_test_eli.drop(discretize,axis =1)
X_test_dis = pd.concat([X_test_dis,r],axis =1)
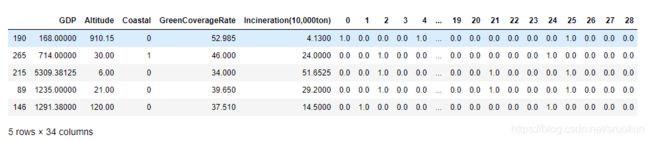
#查看转换后的格式
display(X_train_dis.head())

这样，我们就可以对转换后的数据进行训练了。

lr.fit(X_train_dis,y_train)
print(lr.score(X_train_dis,y_train))
print(lr.score(X_test_dis,y_test))

0.6892388692774563
0.6546062348355675

8、残差图分析

残差就是模型预测值与真实值之间的差异，我们可以绘制残差图，来对回归模型进行评估。残差图的横坐标为预测值，纵坐标为残差值。

8.1、异方差性

对于一个好的回归模型，误差应该是随机分布的，因此残差也应随机分布于中心线附近。如果我们从残差图中找到规律，这意味着模型遗漏了某些能够影响残差的解释信息。

异方差性，是指残差具有明显的方差不一致性，这里我们异常值处理前后的两组数据，分别训练模型，然后观察残差的效果。

import matplotlib.pyplot as plt
fig,ax = plt.subplots(1,2)
fig.set_size_inches(15,5)
data = [X_train,X_train_dis]
title = ['原始数据','处理后数据']
for d,a,t in zip(data,ax,title):
    model = LinearRegression()
    model.fit(d,y_train)
    y_hat_train = model.predict(d)
    residual = y_hat_train - y_train.values
    a.set_xlabel('预测值')
    a.set_ylabel('残差')
    a.axhline(y=0,color='red')
    a.set_title(t)
    sns.scatterplot(x=y_hat_train,y=residual,ax=a)

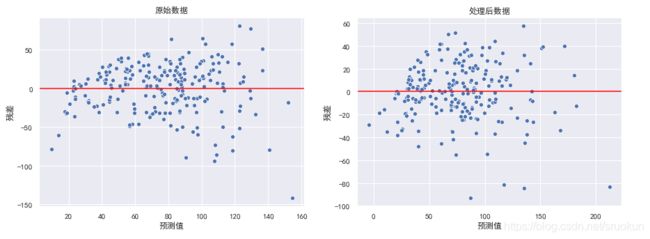
在右图中，我们发现随着预测值的增大，模型的误差也在增大，对于此情况，我们可以使用对目标y值取对数的方式处理。

model = LinearRegression()
y_train_log = np.log(y_train)
y_test_log = np.log(y_test)
model.fit(X_train,y_train_log)

y_hat_train = model.predict(X_train)
residual = y_hat_train - y_train_log.values
plt.xlabel('预测值')
plt.ylabel('残差')
plt.axhline(y=0,color='red')
sns.scatterplot(x=y_hat_train,y=residual)

此时，异方差性得到解决。同时，模型的效果也可能会得到一定的提升。

8.2、离群点

如果是简单线性回归，我们通过绘制回归线，就可以轻松的看出是否存在一些离散点。然而，对于多元线回归，其回归线
已经扩展成为超平面，我们无法通过可视化来进行预测。
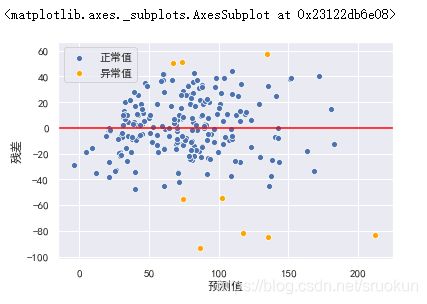
然而，我们可以通过绘制残差图，通过预测值与实际值之间的关系，来检测离群点。

y_hat_train = lr.predict(X_train_dis)
residual = y_hat_train - y_train.values

r = (residual-residual.mean())/residual.std()

plt.xlabel('预测值')
plt.ylabel('残差')
plt.axhline(y=0,color='red')
sns.scatterplot(x=y_hat_train[np.abs(r)<=2],y=residual[np.abs(r)<=2],color='b',label='正常值')
sns.scatterplot(x=y_hat_train[np.abs(r)>2],y=residual[np.abs(r)>2],color='orange',label='异常值')

X_train_dis_filter = X_train_dis[np.abs(r)<=2]
y_train_filter = y_train[np.abs(r)<=2]
lr.fit(X_train_dis_filter,y_train_filter)
print(lr.score(X_train_dis_filter,y_train_filter))
print(lr.score(X_test_dis,y_test))

0.7354141753913532
0.6302724058812208
最后训练模型整体效果比之前好很多。

六、总结

1.空气质量总体分布上来说，南部城市优于北部城市，西部城市优于东部城市。
2.临海城市的空气质量整体上好于内陆城市。
3.是否临海，降雨量与纬度对空气质量指数的影响较大。
4.我国城市平均空气质量指数大致在(70.63 - 80.04)这个区间内，在该区间的可能性概率为95%。
5.通过历史数据，我们可以对空气质量指数进行预测。