opencv图像傅里叶变换

傅里叶变换可以用来分析不同滤波器的频率特性。

 numpy中的傅里叶变换

numpy 中的FFT包可以实现快速傅里叶变换。np.fft.fft2()可以对信号进行频率转换。

"""
函数 np.fft.fft2() 可以对信号频率转换 输出结果是一个复杂的数组。
第一个参数是 输入图像  图像是灰度格式。
第二个参数是可选的, 决定输出数组的大小。
输出数组的大小和输入图像大小一样。如果输出结果比输入图像大
输入图像就需要在进行 FFT 前补0。如果输出结果比输入图像小的话，输入图像就会被切割。
"""
import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('img1.png', 0)
#进行傅里叶变换，频率为0的部分（直流分量）在输出图像的左上角，可以通过np.fft.fftshift()可以将频率为0的部分平移到图像的中心
f = np.fft.fft2(img)
#进行平移，将直流分量平移到图像的中心
fshift = np.fft.fftshift(f)
# 振幅图
magnitude_spectrum = 20 * np.log(np.abs(fshift))

plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

 中心部分更白，这说明低频分量更多。

import cv2
import numpy as np
from matplotlib import pyplot as plt

img=cv2.imread('img2.png',0)
#进行傅立叶变换，并显示结果
fft2 = np.fft.fft2(img)
#将图像变换的原点移动到频域矩形的中心，并显示效果
shift2center = np.fft.fftshift(fft2)
#对傅立叶变换的结果进行对数变换，并显示效果
log_fft2 = np.log(1 + np.abs(fft2))
#对中心化后的结果进行对数变换，并显示结果
log_shift2center = np.log(1 + np.abs(shift2center))
#进行逆平移
f_image = np.fft.ifftshift(shift2center)
#逆变换
image_new = np.fft.ifft2(f_image)
#反变换的结果是复数
image_new = np.abs(image_new)
plt.subplot(2,3,1),plt.imshow(img,'gray'),plt.title('origin')
plt.subplot(2,3,2),plt.imshow(np.abs(fft2),'gray'),plt.title('fft2')
plt.subplot(2,3,3),plt.imshow(np.abs(shift2center),'gray'),plt.title('shift2center')
plt.subplot(2,3,4),plt.imshow(log_fft2,'gray'),plt.title('log_fft2')
plt.subplot(2,3,5),plt.imshow(log_shift2center,'gray'),plt.title('log_shift2center')
plt.subplot(2,3,6),plt.imshow(image_new,'gray'),plt.title('log_shift2center')
plt.show()

 

高通滤波

使用60*60的窗口进行掩膜进行去除低频分量

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('img1.png', 0)
##对图像进行傅里叶变换
f = np.fft.fft2(img)
##将低频分量平移到图像的中心
fshift = np.fft.fftshift(f)

rows, cols = img.shape
crow, ccol = int(rows / 2), int(cols / 2)
##将低频部分置为0。  定义了一个60*60的矩形窗口进行掩膜操作去除低频分量
i=30
fshift[crow - i:crow + i, ccol - i:ccol + i] = 0
##然后将低频分量逆平移部分
f_ishift = np.fft.ifftshift(fshift)
##进行fft逆变换
img_back = np.fft.ifft2(f_ishift)
# 取绝对值
img_back = np.abs(img_back)

#原始的图像
plt.subplot(131), plt.imshow(img, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
##变换的图像
plt.subplot(132), plt.imshow(img_back, cmap='gray')
plt.title('Image after HPF'), plt.xticks([]), plt.yticks([])
plt.subplot(133), plt.imshow(img_back)
plt.title('Result in JET'), plt.xticks([]), plt.yticks([])
plt.show()

 低通滤波

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('img1.png', 0)
##对图像进行傅里叶变换
f = np.fft.fft2(img)
rows, cols = img.shape
crow, ccol = int(rows / 2), int(cols / 2)
##这时高频部分都在图片的中心，将高频部分置为0，实现低通滤波。  定义了一个60*60的矩形窗口进行掩膜操作去除低频分量
i=30
f[crow - i:crow + i, ccol - i:ccol + i] = 0
##进行fft逆变换
img_back = np.fft.ifft2(f)
# 取绝对值
img_back = np.abs(img_back)
#原始的图像
plt.subplot(131), plt.imshow(img, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
##变换的图像
plt.subplot(132), plt.imshow(img_back, cmap='gray')
plt.title('Image after LPF'), plt.xticks([]), plt.yticks([])
plt.subplot(133), plt.imshow(img_back)
plt.title('Result in JET'), plt.xticks([]), plt.yticks([])
plt.show()

 

 opencv傅里叶变换

opencv中相应的函数cv2.dft()  cv2.idft()。输入图像可以首先转换为np.float32格式。输出图像是双通道的，分别为实数部分、虚数部分

"""
OpenCV 中相应的函数是 cv2.dft() 和 cv2.idft()。和前面出的结果 一样 但是是双通道的。
第一个通道是结果的实数部 分
第二个通道是结果的虚数部分。
输入图像先 换成 np.float32 格式
使用函数 cv2.cartToPolar() 它会同时返回幅度和相位。
"""
import numpy as np
import cv2
from matplotlib import pyplot as plt

img = cv2.imread('img1.png', 0)

##输出是双通道，分别为实数部分虚数部分
dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)

dft_shift = np.fft.fftshift(dft)
magnitude_spectrum = 20 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))

plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

 低通滤波

将高频部分去除。就是对图像进行模糊操作。首先构建了一个掩膜，低频区域的地方设置为1，高频区域设置为0.

import numpy as np
import cv2
from matplotlib import pyplot as plt

img = cv2.imread('img1.png', 0)

dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)

dft_shift = np.fft.fftshift(dft)

rows, cols = img.shape
crow, ccol = int(rows / 2), int(cols / 2)

# create a mask first, center square is 1, remaining all zeros
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow - 30:crow + 30, ccol - 30:ccol + 30] = 1

# apply mask and inverse DFT
fshift = dft_shift * mask
f_ishift = np.fft.ifftshift(fshift)
img_back = cv2.idft(f_ishift)
img_back = cv2.magnitude(img_back[:, :, 0], img_back[:, :, 1])

plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(img_back, cmap='gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

import cv2
import numpy as np
from matplotlib import pyplot as plt

# 均值滤波器
mean_filter = np.ones((3, 3))
# 创建高斯滤波器
x = cv2.getGaussianKernel(5, 10)

gaussian = x * x.T
# 不同的边缘检测滤波器
# scharr in x-direction
scharr = np.array([[-3, 0, 3],
                   [-10, 0, 10],
                   [-3, 0, 3]])
# sobel in x direction
sobel_x = np.array([[-1, 0, 1],
                    [-2, 0, 2],
                    [-1, 0, 1]])
# sobel in y direction
sobel_y = np.array([[-1, -2, -1],
                    [0, 0, 0],
                    [1, 2, 1]])
# laplacian
laplacian = np.array([[0, 1, 0],
                      [1, -4, 1],
                      [0, 1, 0]])
filters = [mean_filter, gaussian, laplacian, sobel_x, sobel_y, scharr]
filter_name = ['mean_filter', 'gaussian', 'laplacian', 'sobel_x', 'sobel_y', 'scharr_x']

fft_filters = [np.fft.fft2(x) for x in filters]
fft_shift = [np.fft.fftshift(y) for y in fft_filters]
mag_spectrum = [np.log(np.abs(z) + 1) for z in fft_shift]

for i in range(6):
    plt.subplot(2, 3, i + 1), plt.imshow(mag_spectrum[i], cmap='gray')
    plt.title(filter_name[i]), plt.xticks([]), plt.yticks([])
plt.show()

 

import numpy as np
from matplotlib import pyplot as plt

# 均值滤波器
mean_filter = np.ones((3, 3))

##原来的频谱图
fft_filters = np.fft.fft2(mean_filter)
##经过平移之后的频谱图
fft_shift = np.fft.fftshift(fft_filters)
mag_spectrum = np.log(np.abs(fft_shift) + 1)
hh=np.log(np.abs(fft_filters)+1)
plt.subplot(121)
plt.imshow(hh, cmap='gray')
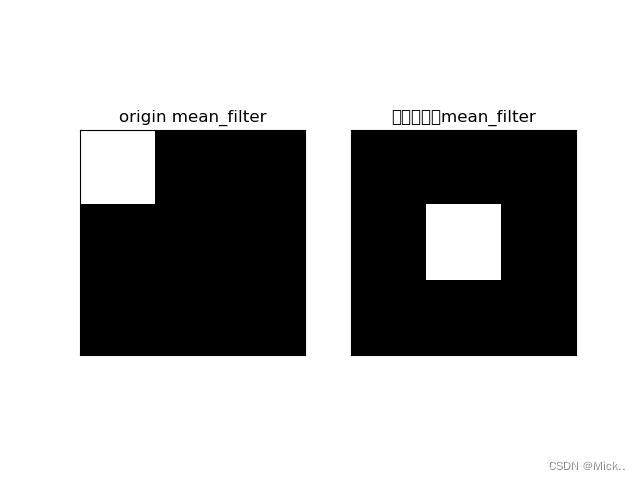
plt.title('origin mean_filter'), plt.xticks([]), plt.yticks([])
plt.subplot(122)
plt.imshow(mag_spectrum, cmap='gray')
plt.title('平移之后的mean_filter'), plt.xticks([]), plt.yticks([])
plt.show()

 

上面的图像是均值滤波器的幅度频谱图。中间部分最亮