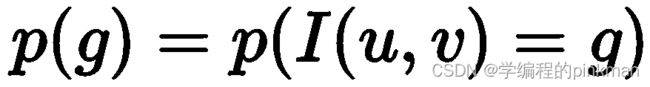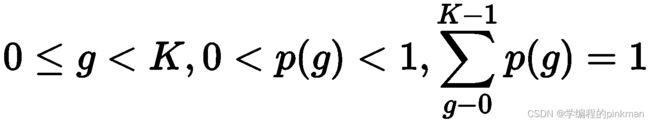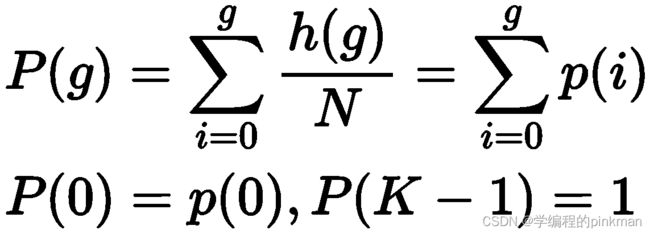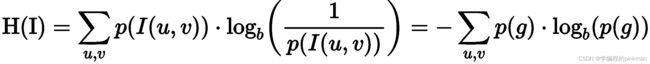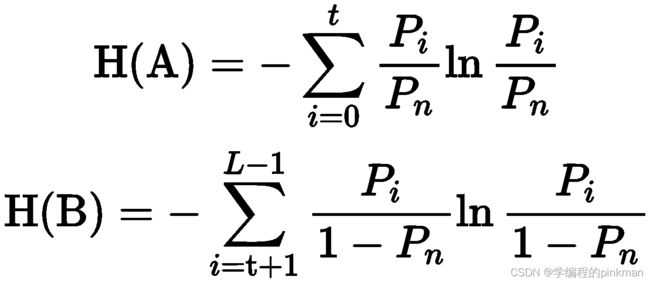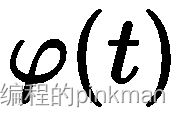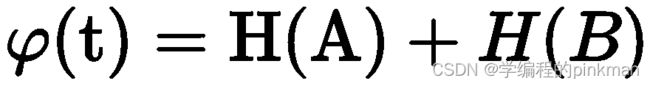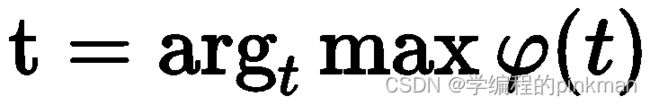基于阈值的图像分割——最大熵阈值分割

最大熵阈值分割

        最大熵阈值法和OTSU算法类似，假设将图像分为背景和前景两个部分。熵代表信息量，图像信息量越大，熵就越大，最大熵算法就是找出一个最佳阈值使得背景与前景两个部分熵之和最大。         熵是信息论中一个重要的概念，这种方法常用于数据压缩领域。熵是一种统计测量方法，用以确定随机数据源中所包含的信息数量。例如，包含有N个像素的图像I，可以解释为包含有N个符号的信息，每一个符号的值都独立获取于有限范围K（e.g.（0,256））中的不同灰度值。
将数字图像建模为一种随机信号处理，意味着必须知道图像灰度中每一个灰度g所发生的概率，即：

        因为所有概率应该事先知道，所以这些概率也称为先验概率。对于K个不同灰度值g=0,…,K-1的概率向量可以表示为：

        上述概率向量也称为概率分布或称为概率密度函数(pdf)。实际数字图像处理应用当中，先验的概率通常是不知道的，但是这些概率可以通过在一幅图像或多幅图像中观察对应灰度值所发生的频率，从而估算出其概率。图像概率密度函数p(g)可以通过归一化其对应的直方图获得其概率，即：

 ，对应的累积概率分布函娄数(cdf),可表示为:

         数字图像中给定一个估算的概率密度函数p(g)，数字图像中的熵定义为：

         约束条件为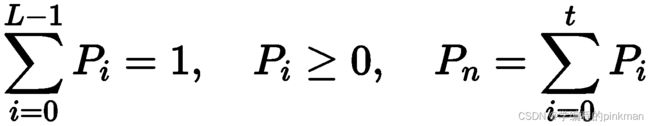，b常取2，I(u，v)为灰度值，假设阈值为t，A为{0，1，2，...,t}的灰度分布，B为{t+1，t+2，...,L-1}的灰度分布，则两个概率密度相关的熵分别为H(A)和 H(B)，由上式计算得到:

         定义函数为 H(A)和H(B)的和:

 最佳阈值为:

 opencv代码：(两个实现方式，MaxEntropyFast是提升了效率的函数)

#include 
#include 

const double g_EPSINON = 0.00001;
int MaxEntropy(const cv::Mat& src, cv::Mat& dst, int thresh, int factor)
{
	const int k_Grayscale = 256;
	double hist[k_Grayscale] = { 0.0 };
	int r = src.rows;
	int c = src.cols;
	for (int i = 0; i < r; ++i)
	{
		const uchar* ptr = src.ptr(i);
		for (int j = 0; j < c; ++j)
			hist[ptr[j]]++;
	}

	double probability = 0.0; //概率
	double maxEntropy = DBL_MIN; //最大熵
	int totalpix = r * c;
	for (int i = 0; i < k_Grayscale; ++i)
	{
		//计算背景像素数
		double backgroundpix = 0;
		for (int j = 0; j <= i; ++j)
			backgroundpix += hist[j];
		//计算背景熵
		double H0 = 0.0; //背景熵
		if (backgroundpix > 0)
		{
			for (int j = 0; j <= i; ++j)
			{
				probability = hist[j] / backgroundpix;
				if (probability > g_EPSINON)
					H0 += -probability * log(probability);
			}
		}

		//计算前景像素数
		double frontpix = totalpix - backgroundpix;
		//计算前景熵
		double H1 = 0.0; //前景熵
		if (frontpix > 0)
		{
			for (int k = i + 1; k < k_Grayscale; ++k)
			{
				probability = hist[k] / frontpix;
				if (probability > g_EPSINON)
					H1 += -probability * log(probability);
			}
		}

		//计算最大熵
		if (H0 + H1 > maxEntropy)
		{
			maxEntropy = H0 + H1;
			thresh = i;
		}
	}

	thresh += factor;
	//阈值处理
	src.copyTo(dst);
	for (int i = 0; i < r; ++i) {
		uchar* ptr = dst.ptr(i);
		for (int j = 0; j < c; ++j) {
			if (ptr[j]> thresh)
				ptr[j] = 255;
			else
				ptr[j] = 0;
		}
	}
	return thresh;
}


void MakeTable(double *S0, double *S1, double *normalizeHist, int histSize)
{
	double s0 = 0.0;
	for (int i = 0; i < histSize; i++)
	{
		if (normalizeHist[i] > g_EPSINON)
			s0 = s0 + normalizeHist[i] * log(normalizeHist[i]);
		S0[i] = s0;
	}

	double s1 = 0.0;
	for (int i = histSize - 1; i >= 0; i--)
	{
		S1[i] = s1;
		if (normalizeHist[i] > g_EPSINON)
			s1 = s1 + normalizeHist[i] * log(normalizeHist[i]);

	}
}

int MaxEntropyFast(const cv::Mat& src, cv::Mat& dst, int thresh, int factor)
{
	const int k_GrayScale = 256;
	int hist[k_GrayScale] = { 0 };
	int r = src.rows;
	int c = src.cols;
	for (int i = 0; i < r; ++i) {
		const uchar* ptr = src.ptr(i);
		for (int j = 0; j < c; ++j)
			hist[ptr[j]]++;
	}

	double normalizeHist[256] = { 0.0 }, sum = (double)(r * c);
	for (int i = 0; i < k_GrayScale; i++)
		normalizeHist[i] = hist[i] / sum;

	double S0[256] = { 0 }, S1[256] = { 0 };
	MakeTable(S0, S1, normalizeHist, k_GrayScale);

	double H01 = 0.0, H0 = 0.0, H1 = 0.0, P1 = 0.0, P0 = 0.0, Hmax = DBL_MIN;
	for (int q = 0; q < k_GrayScale; q++)
	{
		P0 += normalizeHist[q];
		if (P0 > g_EPSINON)
			H0 = -(1.0 * S0[q]) / P0 + log(P0);
		else
			H0 = 0.0;

		P1 = 1.0 - P0;
		if (P1 > g_EPSINON)
			H1 = -(1.0 * S1[q]) / P1 + log(P1);
		else
			H1 = 0.0;

		H01 = H0 + H1;

		if (H01 > Hmax)
		{
			Hmax = H01;
			thresh = q;
		}

	}

	thresh += factor;
	//阈值处理
	src.copyTo(dst);
	for (int i = 0; i < r; ++i) {
		uchar* ptr = dst.ptr(i);
		for (int j = 0; j < c; ++j) {
			if (ptr[j] > thresh)
				ptr[j] = 255;
			else
				ptr[j] = 0;
		}
	}
	return thresh;
}


int main()
{
	cv::Mat src = cv::imread("D:\\graduate_project\\photo\\jinxiang_caij.jpg");
	imshow("src原", src);
	if (src.empty()) {
		return -1;
	}
	if (src.channels() > 1)
		cv::cvtColor(src, src, CV_RGB2GRAY);

	cv::Mat dst, dstOtsu;
	int thresh = 0;
	double t2 = (double)cv::getTickCount();
	thresh = MaxEntropy(src, dst, thresh, 0); //Max_Entropy
	std::cout << "MaxEntropyThresh=" << thresh << std::endl;
	t2 = (double)cv::getTickCount() - t2;
	double time2 = (t2 *1000.) / ((double)cv::getTickFrequency());
	std::cout << "MaxEntropyProcess=" << time2 << " ms. " << std::endl << std::endl;

	cv::Mat dstFast;
	thresh = 0;
	t2 = (double)cv::getTickCount();
	thresh = MaxEntropyFast(src, dstFast, thresh, 0); //Max_Entropy
	std::cout << "MaxEntropyFastThresh=" << thresh << std::endl;
	t2 = (double)cv::getTickCount() - t2;
	time2 = (t2 *1000.) / ((double)cv::getTickFrequency());
	std::cout << "MaxEntropyFastProcess=" << time2 << " ms. " << std::endl << std::endl;


	double  Otsu = 0;
	Otsu = cv::threshold(src, dstOtsu, Otsu, 255, CV_THRESH_OTSU + CV_THRESH_BINARY);
	std::cout << "OtsuThresh=" << Otsu << std::endl;


	cv::imshow("src", src);
	cv::imshow("dst", dst);
	cv::imshow("dstOtsu", dstOtsu);
	//cv::imwrite("r.jpg",dst);
	cv::waitKey(0);
}

最后的运行结果图：

参考连接：阈值分割算法的对比研究 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/380931387

(34条消息) 图像分割之最大熵阈值分割_阿兵-AI医疗的博客-CSDN博客_基于最大熵的图像分割https://blog.csdn.net/webzhuce/article/details/115413826?spm=1001.2014.3001.5502