图像分割——阈值分割二值化算法汇总
一、Otsu、Niblack、Sauvola
1、Otsu
略
2、Sauvola--局部二值化算法
之前接触过全局二值化(OTSU算法),还有OPENCV提供的自适应二值化,最近又了解到一种新的局部二值化算法,Sauvola算法。
值得注意的是,计算r×r邻域内像素值的时候,一种优化的策略是,使用OPENCV提供的积分图,计算整张图像的积分图,那么计算r×r区域内的均值可以在常数时间内实现。
CV_EXPORTS_W void integral( InputArray src, OutputArray sum, int sdepth = -1 );
我们常见的图像二值化算法大致可分为全局阈值方法与局部阈值方法这两种类型。其中OTSU算法是全局阈值的代表,而Sauvola算法则是局部阈值方法的标杆。Sauvola算法的输入是灰度图像,它以当前像素点为中心,根据当前像素点邻域内的灰度均值与标准方差来动态计算该像素点的阈值。
假定当前像素点的坐标为(x,y),以该点为中心的领域为r*r,g(x,y)表示(x,y)处的灰度值,Sauvola算法的步骤为:
sauvola是一种考虑局部均值亮度的图像二值化方法, 以局部均值为基准在根据标准差做些微调.算法实现上一般用积分图方法
来实现.这个方法能很好的解决全局阈值方法的短板—光照不均图像二值化不好的问题.
Sauvola算法C#代码讲解
本文中Sauvola算法的代码更新了部分注释,给出阈值计算公式的推导过程:
本文贴出的代码在图像尺寸比较大时,图像积分的计算值会超出图像积分存储量的数据类型。若您需要用本文发布的代码,还请检查图像尺寸是否会令代码中相关变量溢出,若有请自行修改为合适的变量,谢谢!
C#代码:
///
/// 实现Sauvola算法实现图像二值化
///
/// 用于存储二值化完成的图像
/// 用于存储等待二值化完成的灰度图像
public static void Sauvola(Byte[,] bin_image, Byte[,] gray_image)
{
//以当前像素点为中心的邻域的宽度
int w = 40;
//使用者自定义的修正系数
double k = 0.3;
//邻域边界距离中心点的距离
int whalf = w >> 1;
int MAXVAL = 256;
int image_width = gray_image.GetLength(0);
int image_height = gray_image.GetLength(1);
int[,] integral_image = new int[image_width, image_height];
int[,] integral_sqimg = new int[image_width, image_height];
int[,] rowsum_image = new int[image_width, image_height];
int[,] rowsum_sqimg = new int[image_width, image_height];
int xmin,ymin,xmax,ymax;
double diagsum,idiagsum,diff,sqdiagsum,sqidiagsum,sqdiff,area;
double mean,std,threshold;
for (int j = 0; j < image_height; j++)
{
rowsum_image[0, j] = gray_image[0, j];
rowsum_sqimg[0, j] = gray_image[0, j] * gray_image[0, j];
}
for (int i = 1; i < image_width; i++)
{
for (int j = 0; j < image_height; j++)
{
//计算图像范围内任意宽度窗口(邻域)的灰度值之和
rowsum_image[i, j] = rowsum_image[i - 1, j] + gray_image[i, j];
//计算图像范围内任意宽度窗口(邻域)的灰度值平方之和
rowsum_sqimg[i, j] = rowsum_sqimg[i - 1, j] + gray_image[i, j] * gray_image[i, j];
}
}
for (int i = 0; i < image_width; i++)
{
integral_image[i, 0] = rowsum_image[i, 0];
integral_sqimg[i, 0] = rowsum_sqimg[i, 0];
}
for (int i = 0; i < image_width; i++)
{
for (int j = 1; j < image_height; j++)
{
//计算图像范围内任意宽度窗口(邻域)的灰度值的积分
integral_image[i, j] = integral_image[i, j - 1] + rowsum_image[i, j];
//计算图像范围内任意宽度窗口(邻域)的灰度值平方的积分
integral_sqimg[i, j] = integral_sqimg[i, j - 1] + rowsum_sqimg[i, j];
}
}
//Calculate the mean and standard deviation using the integral image
for(int i=0; i= 0):
// we'll prove that (xmax-xmin+1) > 0,
// (ymax-ymin+1) is analogous
// It's the same as to prove: xmax >= xmin
// image_width - 1 >= 0 since image_width > i >= 0
// i + whalf >= 0 since i >= 0, whalf >= 0
// i + whalf >= i - whalf since whalf >= 0
// image_width - 1 >= i - whalf since image_width > i
// --IM
if (area <= 0)
throw new Exception("Binarize: area can't be 0 here");
if (xmin == 0 && ymin == 0)
{ // Point at origin
diff = integral_image[xmax, ymax];
sqdiff = integral_sqimg[xmax, ymax];
}
else if (xmin == 0 && ymin > 0)
{ // first column
diff = integral_image[xmax, ymax] - integral_image[xmax, ymin - 1];
sqdiff = integral_sqimg[xmax, ymax] - integral_sqimg[xmax, ymin - 1];
}
else if (xmin > 0 && ymin == 0)
{ // first row
diff = integral_image[xmax, ymax] - integral_image[xmin - 1, ymax];
sqdiff = integral_sqimg[xmax, ymax] - integral_sqimg[xmin - 1, ymax];
}
else
{ // rest of the image
diagsum = integral_image[xmax, ymax] + integral_image[xmin - 1, ymin - 1];
idiagsum = integral_image[xmax, ymin - 1] + integral_image[xmin - 1, ymax];
//以(i,j)为中心点的w邻域内灰度值的积分
diff = diagsum - idiagsum;
sqdiagsum = integral_sqimg[xmax, ymax] + integral_sqimg[xmin - 1, ymin - 1];
sqidiagsum = integral_sqimg[xmax, ymin - 1] + integral_sqimg[xmin - 1, ymax];
//以(i,j)为中心点的w邻域内灰度值平方的积分
sqdiff = sqdiagsum - sqidiagsum;
}
//以(i,j)为中心点的w邻域内的灰度均值
mean = diff/area;
//以(i,j)为中心点的w邻域内的标准方差
std = Math.Sqrt((sqdiff - diff*diff/area)/(area-1));
//根据Sauvola计算公式和以(i,j)为中心点的w邻域内的灰度均值与标准方差来计算当前点(i,j)的二值化阈值
threshold = mean*(1+k*((std/128)-1));
//根据当前点的阈值对当前像素点进行二值化
if(gray_image[i,j] < threshold)
bin_image[i,j] = 0;
else
bin_image[i,j] = (byte)(MAXVAL-1);
}
}
} 代码要注意下面几点:
1 计算区域像素和,几乎使用积分图技术是必然的选择.
2 标准差的表示方法: std = sqrt((sqdiff - diff*diff / area) / (area - 1)) 终于感到高等代数没有白学,
3 判定方程 threshold = mean*(1 + k*((std / 128) - 1)). 首先均值是基础, 如果标准差大写,阈值就会大些,标准差小些,阈值就会小些.
这个方法对一些不是光照不均的图片有时候效果不好,现在还在找较好的方法,初步打算先用全局均值做二值化,如何效果不好再用局部均值的方法.
3、Niblack
在二值化的操作中,用的比较多的就是全局阈值话OTSU(大津法)和局部阈值NiBlack,Niblack方法是一种简单有效的动态阈值分割方法,修改得到最佳参数之后的效果比大津法要好,因为大津法是根据整个图像来确定一个阈值,而Niblack则是在不同的R*R区域会有不同的阈值。
Niblack的基本思想是:对于图像的每一个像素点,在rxr领域空问里,计算该像素点领域方位内其他像素点的均值和方差。然后利用公式(1)进行二值化。
其中,T(x,y)是阈值,k是预先设定的修正值,图像为f(x,y),均值为m(x,y),方差为s(x,y)。
使用Niblack法的优点在于:
对每一个像素点都独立的跟据此像素点的邻域的情况来计算门限,对于和邻域均值m(x,y)相近的像素点判断为背景而反之判断为前景;而具体相近到什么程度由标准差s(X’y)和修正系数k来决定,这保证了这种的方法的灵活性。
使用Niblack法的不足在于:
由于要利用域r×r模板遍历图像,导致边界区域(r-1)/2的像素范围内无法求取阈值;同时当进行图像遍历时,如果域r×r范围内都是背景,经NIBLACK计算后必有一部分被确定为目标,产生伪噪声。
总之,用Niblack方法进行图像分割时,选择的处理模板窗口R*R大小的选择很关键,选择的空间太小,则噪声抑制的效果不理想,目标主体不够突出,选择的空间太大,则目标的细节会被去除而丢失信息。
python代码
import matplotlib
import matplotlib.pyplot as plt
from skimage.data import page
from skimage.filters import (threshold_otsu, threshold_niblack,
threshold_sauvola)
matplotlib.rcParams['font.size'] = 9
image = page()
binary_global = image > threshold_otsu(image)
window_size = 25
thresh_niblack = threshold_niblack(image, window_size=window_size, k=0.8)
thresh_sauvola = threshold_sauvola(image, window_size=window_size)
binary_niblack = image > thresh_niblack
binary_sauvola = image > thresh_sauvola
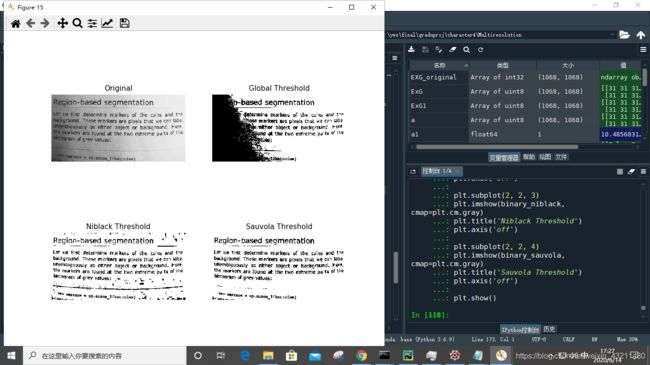
plt.figure(figsize=(8, 7))
plt.subplot(2, 2, 1)
plt.imshow(image, cmap=plt.cm.gray)
plt.title('Original')
plt.axis('off')
plt.subplot(2, 2, 2)
plt.title('Global Threshold')
plt.imshow(binary_global, cmap=plt.cm.gray)
plt.axis('off')
plt.subplot(2, 2, 3)
plt.imshow(binary_niblack, cmap=plt.cm.gray)
plt.title('Niblack Threshold')
plt.axis('off')
plt.subplot(2, 2, 4)
plt.imshow(binary_sauvola, cmap=plt.cm.gray)
plt.title('Sauvola Threshold')
plt.axis('off')
plt.show()二、Bernsen
import cv2 as cv
import numpy as np
def rgb2gray(img):
h=img.shape[0]
w=img.shape[1]
grayimg=np.zeros((h,w),np.uint8)
for i in range (h):
for j in range (w):
grayimg[i,j]=0.144*img[i,j,0]+0.587*img[i,j,1]+0.299*img[i,j,2]
return grayimg
def bernsens(img):
h=img.shape[0]
w=img.shape[1]
img1=np.zeros((h,w),np.uint8)
for i in range (1,h-1):
for j in range (1,w-1):
matrix=np.zeros((3,3),np.uint8)
for k in range (-1,2):
for l in range (-1,2):
matrix[k+1,l+1]=img[i+k,j+l]
threshold=(np.max(matrix)+np.min(matrix))/2
if img[i,j]>=threshold:
img1[i,j]=255
else:
img1[i,j]=0
return img1
image=cv.imread("D:/Testdata/a.png")
grayimage=rgb2gray(image)
thresholdimage=bernsens(grayimage)
cv.imshow("image",image)
cv.imshow("grayimage",grayimage)
cv.imshow("thresholdimage",thresholdimage)
cv.waitKey(0)
cv.destroyAllWindows()
参考资料:
参考文献1:《Efficient multiscale Sauvola’s binarization》 密码: diu8,该文献先给出Sauvola算法的计算公式,然后提出了该算法的几点局限性并分别给出了改善对策;
参考文献2:《Adaptive document image binarization》密码: fhaj,该文献的作者是J. Sauvola,它分别讲述了图像中非文字部分与文字部分的二值化方法,文字部分的二值化方法即《Sauvola 实现图像二值化》中代码所实现的Sauvola算法。该文献中提到Sauvola算法是Niblack算法的改进版本,有两个公式来源于Niblack算法。《An Introduction to Image Processing》(作者:W. Niblack,1986年出版)一书中有详细讲述Niblack算法,可惜我遍寻网络,也没有找到该书的电子版,全国图书馆咨询联盟,谷歌图书以及多个外文书库都仅仅是收录了书名,并无内容的电子版。
参考文献3:《基于改进 Otsu和 Niblack的图像二值化方法》密码: mfw4,还好我在文献3中找到了Sauvola算法中沿用的Niblack算法的公式。
1.第一次做MathOCR遇到的参考文献:
《图片中印刷体数学公式的自动识别》陈颂光
2.中文的的链接来自,追溯不到原文:
Sauvola算法公式推导 - LiveZingy
3.英文文献:值得参考的标准
Efficient implementation of local adaptive thresholding techniques using integral images
PDF链接为:https://pdfs.semanticscholar.org/8130/a9499715d22468492c3786c34ba1ba0b4ed3.pdf
4.Matlab代码参考
http://freesourcecode.net/matlabprojects/59687/sauvola-local-image-thresholding-in-matlab#.Wzsk2oq-vcs
5.sauvola二值化算法研究 - guopengfei - 博客园