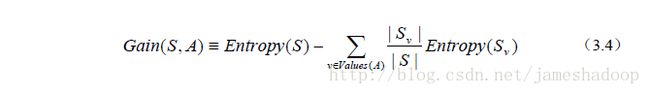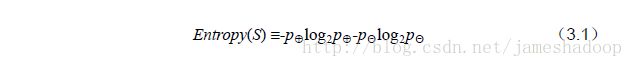决策树算法 java_决策树算法原理及JAVA实现(ID3)

0 引言

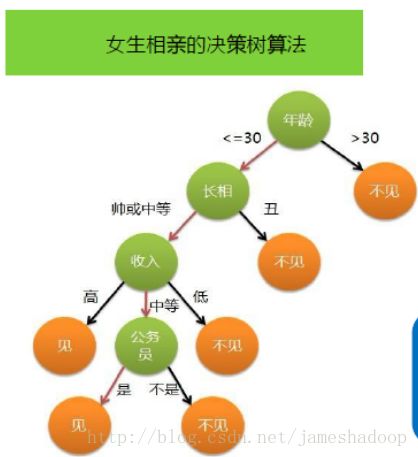
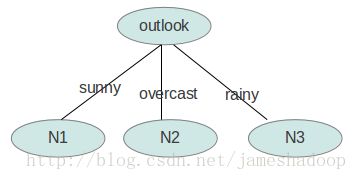
决策树的目的在于构造一颗树像下面这样的树。

图1

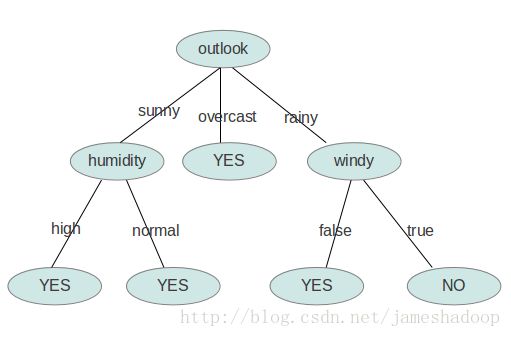
图2

1. 如何构造呢？

1.1   参考资料。

本例以图2为例，并参考了以下资料。

写的东西非常经典。

(3)机器学习(Tom.Mitchell著) 第三章 决策树，里面详细介绍了信息增益的计算，和熵的计算。建议大家参考

1.2 数据集(训练数据集)

outlook

temperature

humidity

windy

play

sunny

hot

high

FALSE

no

sunny

hot

high

TRUE

no

overcast

hot

high

FALSE

yes

rainy

mild

high

FALSE

yes

rainy

cool

normal

FALSE

yes

rainy

cool

normal

TRUE

no

overcast

cool

normal

TRUE

yes

sunny

mild

high

FALSE

no

sunny

cool

normal

FALSE

yes

rainy

mild

normal

FALSE

yes

sunny

mild

normal

TRUE

yes

overcast

mild

high

TRUE

yes

overcast

hot

normal

FALSE

yes

rainy

mild

high

TRUE

no

1.3 构造原则—选信息增益最大的

从图中知，一共有四个属性，outlook     temperature    humidity  windy，首先选哪一个作为树的第一个节点呢。答案是选信息增益越大的作为开始的节点。信息增益的计算公式如下：

Entropy(s)是熵，S样本集，Sv是子集。熵的计算公式如下：

举例：

根据以上的数据，我们只知道新的一天打球的概率是9/14，不打的概率是5/14。此时的熵为

对每项指标分别统计：在不同的取值下打球和不打球的次数。

table 2

outlook

temperature

humidity

windy

play

yes

no

yes

no

yes

no

yes

no

yes

no

sunny

2

3

hot

2

2

high

3

4

FALSE

6

2

9

5

overcast

4

0

mild

4

2

normal

6

1

TRUR

3

3

rainy

3

2

cool

3

1

下面我们计算当已知变量outlook的值时，信息熵为多少。

outlook=sunny时，2/5的概率打球，3/5的概率不打球。entropy=0.971

outlook=overcast时，entropy=0

outlook=rainy时，entropy=0.971

而根据历史统计数据，outlook取值为sunny、overcast、rainy的概率分别是5/14、4/14、5/14，所以当已知变量outlook的值时，信息熵为：5/14 × 0.971 + 4/14 × 0 + 5/14 × 0.971 = 0.693

这样的话系统熵就从0.940下降到了0.693，信息增溢gain(outlook)为0.940-0.693=0.247

同样可以计算出gain(temperature)=0.029，gain(humidity)=0.152，gain(windy)=0.048。

gain(outlook)最大(即outlook在第一步使系统的信息熵下降得最快)，所以决策树的根节点就取outlook。

1.4 为什么选信息增益最大的？

根据参考资料(2)的结论是：信息增益量越大，这个属性作为一棵树的根节点就能使这棵树更简洁(2)

1.5 递归：

接下来要确定N1取temperature、humidity还是windy?在已知outlook=sunny的情况，根据历史数据，我们作出类似table 2的一张表，分别计算gain(temperature)、gain(humidity)和gain(windy)，选最大者为N1。

依此类推，构造决策树。当系统的信息熵降为0时，就没有必要再往下构造决策树了，此时叶子节点都是纯的--这是理想情况。最坏的情况下，决策树的高度为属性(决策变量)的个数，叶子节点不纯(这意味着我们要以一定的概率来作出决策)。

1.6 递归结束的条件：

如果Examples都为正，那么返回label =+ 的单结点树Root ，熵为0

 如果Examples都为反，那么返回label =- 的单结点树Root ，熵为0

 如果Attributes为空，那么返回单结点树Root，label=Examples中最普遍的

2. 伪代码

3. java 实现

此仅贴主要的代码，源码请到我的github下载：

package sequence.machinelearning.decisiontree.myid3;

import java.io.BufferedReader;

import java.io.File;

import java.io.FileReader;

import java.io.FileWriter;

import java.io.IOException;

import java.util.ArrayList;

import java.util.HashMap;

import java.util.Iterator;

import java.util.LinkedList;

import java.util.List;

import java.util.Map;

import java.util.regex.Matcher;

import java.util.regex.Pattern;

import java.util.LinkedList;

public class MyID3 {

private static LinkedList attribute = new LinkedList(); // 存储属性的名称

private static LinkedList> attributevalue = new LinkedList>(); // 存储每个属性的取值

private static LinkedList data = new LinkedList();; // 原始数据

public static final String patternString = "@attribute(.*)[{](.*?)[}]";

public static String[] yesNo;

public static TreeNode root;

/**

*

* @param lines 传入要分析的数据集

* @param index 哪个属性？attribute的index

*/

public Double getGain(LinkedList lines,int index){

Double gain=-1.0;

List li=new ArrayList();

//统计Yes No的次数

for(int i=0;i

Double sum=0.0;

for(int j=0;j

String[] line=lines.get(j);

//data为结构化数据,如果数据最后一列==yes,sum+1

if(line[line.length-1].equals(yesNo[i])){

sum=sum+1;

}

}

li.add(sum);

}

//计算Entropy(S)计算Entropy(S) 见参考书《机器学习 》Tom.Mitchell著 第3.4.1.2节

Double entropyS=TheMath.getEntropy(lines.size(), li);

//下面计算gain

List la=attributevalue.get(index);

List lasv=new ArrayList();

for(int n=0;n

String attvalue=la.get(n);

//统计Yes No的次数

List lisub=new ArrayList();//如：sunny 是yes时发生的次数，是no发生的次数

Double Sv=0.0;//公式3.4中的Sv 见参考书《机器学习(Tom.Mitchell著)》

for(int i=0;i

Double sum=0.0;

for(int j=0;j

String[] line=lines.get(j);

//data为结构化数据,如果数据最后一列==yes,sum+1

if(line[index].equals(attvalue)&&line[line.length-1].equals(yesNo[i])){

sum=sum+1;

}

}

Sv=Sv+sum;//计算总数

lisub.add(sum);

}

//计算Entropy(S) 见参考书《机器学习(Tom.Mitchell著)》

Double entropySv=TheMath.getEntropy(Sv.intValue(), lisub);

//

Point p=new Point();

p.setSv(Sv);

p.setEntropySv(entropySv);

lasv.add(p);

}

gain=TheMath.getGain(entropyS,lines.size(),lasv);

return gain;

}

//寻找最大的信息增益,将最大的属性定为当前节点，并返回该属性所在list的位置和gain值

public Maxgain getMaxGain(LinkedList lines){

if(lines==null||lines.size()<=0){

return null;

}

Maxgain maxgain = new Maxgain();

Double maxvalue=0.0;

int maxindex=-1;

for(int i=0;i

Double tmp=getGain(lines,i);

if(maxvalue< tmp){

maxvalue=tmp;

maxindex=i;

}

}

maxgain.setMaxgain(maxvalue);

maxgain.setMaxindex(maxindex);

return maxgain;

}

//剪取数组

public LinkedList filterLines(LinkedList lines, String attvalue, int index){

LinkedList newlines=new LinkedList();

for(int i=0;i

String[] line=lines.get(i);

if(line[index].equals(attvalue)){

newlines.add(line);

}

}

return newlines;

}

public void createDTree(){

root=new TreeNode();

Maxgain maxgain=getMaxGain(data);

if(maxgain==null){

System.out.println("没有数据集，请检查!");

}

int maxKey=maxgain.getMaxindex();

String nodename=attribute.get(maxKey);

root.setName(nodename);

root.setLiatts(attributevalue.get(maxKey));

insertNode(data,root,maxKey);

}

/**

*

* @param lines 传入的数据集，作为新的递归数据集

* @param node 深入此节点

* @param index 属性位置

*/

public void insertNode(LinkedList lines,TreeNode node,int index){

List liatts=node.getLiatts();

for(int i=0;i

String attname=liatts.get(i);

LinkedList newlines=filterLines(lines,attname,index);

if(newlines.size()<=0){

System.out.println("出现异常，循环结束");

return;

}

Maxgain maxgain=getMaxGain(newlines);

double gain=maxgain.getMaxgain();

Integer maxKey=maxgain.getMaxindex();

//不等于0继续递归，等于0说明是叶子节点，结束递归。

if(gain!=0){

TreeNode subnode=new TreeNode();

subnode.setParent(node);

subnode.setFatherAttribute(attname);

String nodename=attribute.get(maxKey);

subnode.setName(nodename);

subnode.setLiatts(attributevalue.get(maxKey));

node.addChild(subnode);

//不等于0，继续递归

insertNode(newlines,subnode,maxKey);

}else{

TreeNode subnode=new TreeNode();

subnode.setParent(node);

subnode.setFatherAttribute(attname);

//叶子节点是yes还是no?取新行中最后一个必是其名称,因为只有完全是yes,或完全是no的情况下才会是叶子节点

String[] line=newlines.get(0);

String nodename=line[line.length-1];

subnode.setName(nodename);

node.addChild(subnode);

}

}

}

//输出决策树

public void printDTree(TreeNode node)

{

if(node.getChildren()==null){

System.out.println("--"+node.getName());

return;

}

System.out.println(node.getName());

List childs = node.getChildren();

for (int i = 0; i < childs.size(); i++)

{

System.out.println(childs.get(i).getFatherAttribute());

printDTree(childs.get(i));

}

}

public static void main(String[] args) {

// TODO Auto-generated method stub

MyID3 myid3 = new MyID3();

myid3.readARFF(new File("datafile/decisiontree/test/in/weather.nominal.arff"));

myid3.createDTree();

myid3.printDTree(root);

}

//读取arff文件，给attribute、attributevalue、data赋值

public void readARFF(File file) {

try {

FileReader fr = new FileReader(file);

BufferedReader br = new BufferedReader(fr);

String line;

Pattern pattern = Pattern.compile(patternString);

while ((line = br.readLine()) != null) {

if (line.startsWith("@decision")) {

line = br.readLine();

if(line=="")

continue;

yesNo = line.split(",");

}

Matcher matcher = pattern.matcher(line);

if (matcher.find()) {

attribute.add(matcher.group(1).trim());

String[] values = matcher.group(2).split(",");

ArrayList al = new ArrayList(values.length);

for (String value : values) {

al.add(value.trim());

}

attributevalue.add(al);

} else if (line.startsWith("@data")) {

while ((line = br.readLine()) != null) {

if(line=="")

continue;

String[] row = line.split(",");

data.add(row);

}

} else {

continue;

}

}

br.close();

} catch (IOException e1) {

e1.printStackTrace();

}

}

}

版权声明：本文为博主原创文章，未经博主允许不得转载。