基于Matlab的数字图像处理实验:直方图均衡化、傅里叶变换、图像平滑、图像锐化
Author:GUET_diadestiny (课内实验,仅供参考借鉴)
1.1 实验题目:图像直方图均衡化算法
掌握直方图均衡化算法的基本原理
1.2 实验内容
- 读取MATLAB自带图像,对该图像进行直方图均衡化,显示处理前后的图像及直方图的变化,附上代码及相关说明。
clc;clear;close all;
path(path,'D:\R2019a\toolbox\images\imdata');
% 读取路径图像信息
im=imread('trees.tif');
figure(1);
% 4*4显示面板
subplot(2,2,1)
% 显示原始图像
imshow(im);
title('ground truth');
subplot(2,2,2);
% 显示原始直方图
imhist(im);
title('Histogram');
% [M,N]=size(im);
subplot(2,2,3);
% 调用直方图均衡化函数,对原图进行均衡化处理并显示
histeq(im);
title('Equalization');
% 显示均衡化处理后图像的直方图
subplot(2,2,4);
new = histeq(im);
imhist(new);
title('Equalization Histogram');
2. 调出直方图均衡化函数,对相应直方图均衡化代码进行分析。
function [out,T] = histeq(a,cm,hgram) %定义histeq均衡化函数
NPTS = 256; %像素点数量
isIntensityImage = false;
if nargin == 1 %输入一个参数a(原始图像)
validateattributes(a,{'uint8','uint16','double','int16','single'}, ...
{'nonsparse'}, mfilename,'I',1); %验证类型
n = 64; % Default n
hgram = ones(1,n)*(numel(a)/n);% 初始化默认直方图向量hgram
n = NPTS;
isIntensityImage = true; %图像灰度标记
elseif nargin == 2 %输入两个参数
if numel(cm) == 1
%HISTEQ(I,N)
validateattributes(a,{'uint8','uint16','double','int16','single'}, ...
{'nonsparse'}, mfilename,'I',1);
validateattributes(cm, {'single','double'},...
{'nonsparse','integer','real','positive','scalar'},...
mfilename,'N',2);
m = cm;
hgram = ones(1,m)*(numel(a)/m); % 初始化默认直方图向量hgram
n = NPTS;
isIntensityImage = true;
elseif size(cm,2) == 3 && size(cm,1) > 1
%HISTEQ(X,map)
if isa(a, 'uint16')
error(message('images:histeq:unsupportedUint16IndexedImages'))
end
validateattributes(a,{'uint8','double','single'}, ...
{'nonsparse'},mfilename,'X',1);
n = size(cm,1);
hgram = ones(1,n)*(numel(a)/n); % 默认匹配直方图初始化
else
%HISTEQ(I,HGRAM)
validateattributes(a,{'uint8','uint16','double','int16','single'}, ...
{'nonsparse'}, mfilename,'I',1);
validateattributes(cm, {'single','double'},...
{'real','nonsparse','vector','nonempty'},...
mfilename,'HGRAM',2);
hgram = cm; %将原始图像直方图设置为用户指定的向量hgram
n = NPTS;
isIntensityImage = true;
end
else
%HISTEQ(X,MAP,HGRAM)
validateattributes(a,{'uint8','double','uint16','single'}, ...
{'nonsparse'},mfilename,'X',1);
if isa(a, 'uint16')
error(message('images:histeq:unsupportedUint16IndexedImages'))
end
validateattributes(hgram, {'single','double'},...
{'real','nonsparse','vector','nonempty'},...
mfilename,'HGRAM',3);
n = size(cm,1);
if length(hgram)~=n
error(message('images:histeq:HGRAMmustBeSameSizeAsMAP'))
end
end
if min(size(hgram)) > 1
error(message('images:histeq:hgramMustBeAVector'))
end
% 归一化目标直方图灰度值,a为原始输入图像,hgram为待匹配的默认直方图。
hgram = hgram*(numel(a)/sum(hgram)); % Set sum = numel(a)
m = length(hgram); %测量hgram长度
% Intensity image or indexed image
if isIntensityImage %是有效灰度图像
classChanged = false;
if isa(a,'int16') %判断类型
classChanged = true;
a = im2uint16(a); %转化为uint类型进行计算
end
%计算累计直方图a,默认按列累计计算Sn,指定灰度级n。
[nn,cum] = computeCumulativeHistogram(a,n);
% 计算灰度变换映射关系S=T(r),将原图像像素值映射到直方图匹配后的值
T = createTransformationToIntensityImage(a,hgram,m,n,nn,cum);
% Mex call is equivalent to:
% b = uint8((255.0*T(a+1));
% or uint16, 65535.0 etc
b = grayxformmex(a, T); %根据映射关系T得到处理后的均衡化图像b
if nargout == 0
if ismatrix(b)
imshow(b);
return;
else
out = a;
return;
end
elseif classChanged
out = im2int16(b);
else
out = b;
end
else
I = ind2gray(a,cm); %将索引图像转换成灰度图像
%计算累计直方图a,默认按列累计计算Sn,指定灰度级n
[nn,cum] = computeCumulativeHistogram(I,n);
% 计算灰度变换映射关系S=T(r),将原图像像素值映射到直方图匹配后的值
T = createTransformationToIntensityImage(a,hgram,m,n,nn,cum);
% 通过扩展(r,g,b)向量来修正colormap
% 计算等效彩色图像像素,转化到ntsc彩色空间
ntsc = rgb2ntsc(cm);
% 对ntsc进行T映射,存储在ntsc的第二列.
ntsc(:,2) = T(floor(ntsc(:,1)*(n-1))+1)';
% 通过相对亮度变化缩放(r,g,b)向量
map = cm.*((ntsc(:,2)./max(ntsc(:,1),eps))*ones(1,3));
map = map ./ (max(max(map,[],2),1) *ones(1,3));
if nargout == 0
if ismatrix(a)
imshow(a,map);
return;
else
out = a;
return;
end
else
out = map;
end
end
function [nn,cum] = computeCumulativeHistogram(img,nbins)
nn = imhist(img,nbins);
%输出统计直方图,nn=[count,x],count对应每一级灰度像素x的个数,并按列累加
cum = cumsum(nn);
function T = createTransformationToIntensityImage(a,hgram,m,n,nn,cum)
% 通过最小化实际累积直方图和期望之间的误差来得到映射关系T
% 生成累计hgram直方图
cumd = cumsum(hgram);
% tol = nn w/ 1st and last element set to 0, then divide by 2 and tile to MxN
tol = ones(m,1)*min([nn(1:n-1),0;0,nn(2:n)])/2;
% 通过累计直方图计算误差
err = (cumd(:)*ones(1,n)-ones(m,1)*cum(:)')+tol;
% 寻找误差超过阈值的数值组合
d = find(err < -numel(a)*sqrt(eps));
if ~isempty(d)
% 设置最大误差
err(d) = numel(a)*ones(size(d));
end
% 映射关系T最小化误差
% T是原图像a到待匹配直方图hgram的bin位映射
% T(oldbinval) = newbinval
[dum,T] = min(err); %#ok
% 归一化映射关系T
T = (T-1)/(m-1);
1.3 实验结果
对原图像均衡化处理前后的效果图以及直方图(横坐标代表灰度值,纵坐标代表对应像素值的个数)如下图所示:
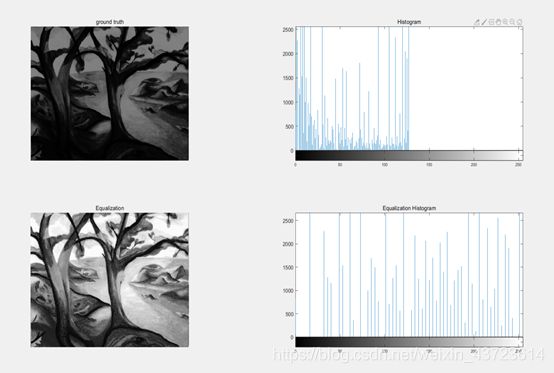
由实验效果图可以看出,原图像在经过直方图均衡化处理后可以增强图像的局部对比度。依据上面的实验原图举例说明,原始图像绝大部分像素点分布在左侧较小灰度值的区域,相对集中造成图像不够清晰。经过均衡化处理后,像素点分布灰度范围变大,均匀分布,对比度增强,清晰度提高,所以直方图均衡化处理对于整体偏暗或者整体偏亮的图像是一种有效的图像增强方法。
2.1 实验题目:傅立叶变换及逆变换算法
掌握傅立叶变换的基本原理和实现算法
2.2 实验内容
调入图像,对图像做傅里叶变换及频谱中心搬移,编写代码实现上述实验举例过程并显示。
clc;clear;close all;
path(path,'D:\R2019a\toolbox\images\imdata');
% 读取路径图像信息
img=imread('sherlock.jpg');
subplot(2,2,1);
imshow(img);
title('原始图');
%将RGB图像转变成灰度图像
ff=rgb2gray(img);
%傅里叶变换
F=fft2(ff);
%求出复数矩阵的模并缩放
F1=log(abs(F)+1);
subplot(2,2,2);
imshow(F1,[]);
title('傅里叶变换频谱图');
%将频谱图中零频率点移至频谱图中间
F1_center=fftshift(F);
%求出复数矩阵的模并缩放
F2=log(abs(F1_center)+1);
subplot(2,2,3);
imshow(F2,[]);
title('频移中心移动后的频谱图');
%频率域反变换到空间域,并取实部,傅里叶逆变换
FR=real(ifft2(ifftshift(F1_center)));
%转化图像类型
new=im2uint8(mat2gray(FR));
subplot(2,2,4);
imshow(new);
title('傅里叶逆变换');
2. 讨论不同的图像内容与频谱之间的对应关系。
通过对比多个输入图像傅里叶变换后的频谱图和原始对应图像后发现,对于含有边缘细节、噪声信号多的图像,其频谱图中高频信号较多;对于模糊、平滑轮廓的图像,其频谱图低频信号较多,对比实验代码如下:
I=imread(‘shadow.tif’);
subplot(2,3,1);
imshow(I); title(‘原图像1’)
%快速傅立叶变换
F=fft2(I);
F=log(abs(F)+1)
%频谱中心搬移
sfftI=fftshift(F);
A=log(abs(sfftI)+1)
subplot(2,3,4);
imshow(A,[]); title(‘对应频谱1’)
I=imread(“pout.tif”);
subplot(2,3,2);
imshow(I); title(‘原图像2’)
%快速傅立叶变换
F=fft2(I);
F=log(abs(F)+1)
%频谱中心搬移
sfftI=fftshift(F);
A=log(abs(sfftI)+1)
subplot(2,3,5);
imshow(A,[]); title(‘对应频谱2’)
I=imread(‘tire.tif’);
subplot(2,3,3);
imshow(I); title(‘原图像3’)
%快速傅立叶变换
F=fft2(I);
F=log(abs(F)+1)
%频谱中心搬移
sfftI=fftshift(F);
A=log(abs(sfftI)+1)
subplot(2,3,6);
imshow(A,[]); title(‘对应频谱3’)
2.3 实验结果
1.对原图像进行傅里叶变换后分别得到频谱图和移动频谱中心的频谱图,以及从频率域反变换到空间域,进行傅里叶逆变换得到逆变换图。如下图所示:

2.分别对不同图像进行傅里叶变换以及频谱中心移动得到各自的频谱图,如下图所示:

由实验效果图可以看出,原图像经过快速傅立叶变换fft后可以得到频谱图;以及通过ffshift函数将零频点移到频谱的中间,可以更直观观察傅立叶变换,傅立叶变换能使从空间域与频率域两个不同角度来分析图像问题。还可以通过ifftshift函数从频率域反映射到空间域,傅里叶逆变换基本还原图像。
在进行傅立叶变换的具体实现中,要注意对fft变换后的频域矩阵数值比较大,一般采用log(abs[F]+1)来对缩放频域,保证映射都在正数范围内,abs函数可以求出复数矩阵的模缩放处理后进行显示。
频谱图表示信号变化的快慢剧烈程度,通过分析不同图像和频谱图的关系时发现,高频信号对应图像的边缘细节,低频信号对应图像的大致概貌和轮廓。因此,对于细节边缘清晰或者噪声较多的图像,经过傅立叶变换后,靠外边的高频信号更多;而对于平滑、具备大体轮廓的图像,经过傅立叶变换后,靠中间的低频信号更多。
3.1 实验题目:图像平滑算法
用MATLAB或VC或Delphi等实现图像平滑的算法。
3.2 实验内容
- 读取一幅图像,对添加噪声的图像用均值滤波、中值滤波和高斯滤波比较,附上代码及相关说明。
clc;clear;close all;
path(path,'D:\R2019a\toolbox\images\imdata');
% 读取彩色图片
im=imread('kobi.png');
subplot(3,3,1);imshow(im);title('ground truth');
% 转化为灰度图像
im = rgb2gray(im);
% 添加均值为0,方差为0.05的高斯噪声
pic_noise1 = imnoise(im,'gaussian',0,0.05);
subplot(3,3,2);imshow(pic_noise1); title('pic1:gaussian noise');
% 添加噪声密度为0.05的椒盐噪声
pic_noise2 = imnoise(im,'salt & pepper',0.05);
subplot(3,3,3);imshow(pic_noise2); title('pic2:salt & pepper noise');
% 3*3模板的均值滤波
template1=(1/9)*[1 1 1;1 1 1;1 1 1];
%利用conv2卷积函数进行滤波计算
show_avg=conv2(double(pic_noise1),double(template1));
subplot(3,3,4);imshow(show_avg,[]); title('average filter in pic1');
% 3*3模板的中值滤波
show_med=medfilt2(pic_noise1,[3,3],'symmetric'); %medfilt2为中值滤波器
subplot(3,3,5);imshow(show_med);title('median filter in pic1');
% 标准差为1的3*3模板的高斯滤波
h=fspecial('gaussian',3,1);%gaussian为高斯低通滤波器
show_gau=imfilter(pic_noise1,h,'conv','symmetric');%imfilter为滤波处理函数
subplot(3,3,6);imshow(show_gau); title('gaussian filter in pic1');
% 3*3模板的均值滤波
template1=(1/9)*[1 1 1;1 1 1;1 1 1];
%利用conv2卷积函数进行滤波计算
show_avg=conv2(double(pic_noise2),double(template1));
subplot(3,3,7);imshow(show_avg,[]); title('average filter in pic2');
% 3*3模板的中值滤波
show_med=medfilt2(pic_noise2,[3,3],'symmetric'); %medfilt2为中值滤波器
subplot(3,3,8);imshow(show_med);title('median filter in pic2');
% 标准差为1的3*3模板的高斯滤波
h=fspecial('gaussian',3,1); %gaussian为高斯低通滤波器
show_gau=imfilter(pic_noise2,h,'conv','symmetric');%imfilter为滤波处理函数
subplot(3,3,9);imshow(show_gau); title('gaussian filter in pic2');
- 调出中值滤波和高斯滤波函数,对相应的代码进行分析。
(1) medfilt2中值滤波函数源码分析:
function b = medfilt2(varargin)
args = matlab.images.internal.stringToChar(varargin); %解析输入参数
%a为待滤波图像,mn向量为滤波模板,padopt为边缘处理选项
[a, mn, padopt] = parse_inputs(args{:});
domain = ones(mn); %大小为m*n的全1矩阵
if (rem(prod(mn), 2) == 1) %取模判断mn滤波模板个数是否为奇数个
tf = hUseIPPL(a, mn, padopt); %padopt是否设置为“symmetric”模式
if tf
b = medianfiltermex(a, [mn(1) mn(2)]);
else
%取出mn矩阵中位数对应的下标order
order = (prod(mn)+1)/2;
%对图像A作顺序统计滤波,A为输入图像矩阵,padopt为边界处理方式
%输出第order个数作为中值滤波的结果
b = ordfilt2(a, order, domain, padopt);
end
else %mn滤波模板个数为偶数个
order1 = prod(mn)/2;%最中间靠左序号
order2 = order1+1;%最中间靠右序号
%对图像A作顺序统计滤波,A为输入图像矩阵,padopt为边界处理方式
%输出第order个数作为中值滤波的结果
b = ordfilt2(a, order1, domain, padopt);
b2 = ordfilt2(a, order2, domain, padopt);
if islogical(b) %判断b类型是否合法
b = b | b2;
else
b = imlincomb(0.5, b, 0.5, b2); %取出平均中间值
end
end
(2) fspecial和imfilter高斯滤波函数源码分析:
function h = fspecial(varargin)
[type, p2, p3] = ParseInputs(varargin{:});%解析输入参数
switch type:%当参数type为'gaussian'高斯滤波时
case 'gaussian' % Gaussian filter
% p2为模板大小,以[m n]形式定义,p3为标准差
siz = (p2-1)/2; %siz为最大行列序号
std = p3;%赋值标准差
%基于siz,std,调用meshgrid函数生成mn模板每个位置的权值
[x,y] = meshgrid(-siz(2):siz(2),-siz(1):siz(1));
% 二维高斯分布中e对应的指数
arg = -(x.*x + y.*y)/(2*std*std);
h = exp(arg);
h(h<eps*max(h(:))) = 0;
%归一化处理
sumh = sum(h(:));
if sumh ~= 0,
h = h/sumh;
end;
end;
从而得到高斯模板,接着调用imfiter函数对任意类型数组或多维图像进行滤波。imfiter (f, w, filtering_mode, boundary_options, size_options),其中, f 为输入图像, w 为滤波掩模, g 为滤波后图像。 filtering_mode 用于指定在滤波过程中是使用“相关”还是“卷积”。 boundary_options 用于处理边界充零问题,边界的大小由滤波器的大小确定。
imfiter函数的核心源码分析如下:
function b = imfilter(varargin):
args = matlab.images.internal.stringToChar(varargin); %解析输入参数
[a, h, boundary, sameSize, convMode, outputShape, do_fcn] = parse_inputs(args{:});
[finalSize, pad] = computeSizes(a, h, sameSize);
if (isSeparable(a, h)&& (numel(size(a))<=3)) %分离滤波器的实部和虚部
% 为了提高计算精度,中间变量用double保存。
class_of_a = class(a);
if ~isa(a,'double')
change_class = true;
a = double(a);
else
change_class = false;
end
%double精度的可分离滤波卷积运算
b = filterDoubleSeparableWithConv(a, h, finalSize, sameSize, convMode, pad, boundary);
if change_class
% For logical inputs, output is rounded and then casted to
% logical - expected behavior
if isequal(class_of_a,'logical')
b = round(b);
end
b = cast(b, class_of_a);
end
else %不分离滤波
if (isequal(class(a),'double') && ismatrix(h) && ismatrix(a)) && isreal(a) && isreal(h)
% 2D image , 2D kernel 进行离滤波卷积运算
b = filterDouble2DWithConv(a, h, finalSize, sameSize, convMode, pad, boundary);
elseif ismember(class(a),{'double','single','uint32','int8'}) && ismatrix(h) &&
numel(size(a))==3
% 3D image , 2D kernel - stack behavior
b = imagesbuiltinImfilter(a, h, boundary, outputShape, do_fcn);
else
% 根据滤波器核的尺寸输入Pad
a = padImage(a,pad,boundary);
b = filterPartOrWhole(a, finalSize, h, pad, sameSize, convMode);
end
end
3.3 实验结果
对添加了高斯噪声和椒盐噪声的原图像分别进行均值滤波、中值滤波和高斯滤波处理,得到的实验图像如下所示:

由实验效果图可以看出均值滤波、中值滤波和高斯滤波三种图像平滑技术对于添加了不同噪声的图片的滤波效果有所不同。均值滤波是典型的线性滤波算法,具有消除边缘尖锐特征,图像模糊化的效果。中值滤波是一种统计排序滤波器,可以一定程度克服线性滤波器带来的图像细节模糊的缺点,由实验效果图可以看出其对于消除椒盐噪声非常有效,并且可以保护边缘信息。而高斯滤波则是对图像进行加权平均,由于高斯滤波模板的权值与位置分布有关,所以可以有效抑制服从正态分布的噪声,如高斯噪声。
4.1 实验题目:图像锐化算法
掌握图像平滑算法的基本原理。
4.2 实验内容
- 对给定的图像分别用一阶梯度算子(罗伯特算子、索贝尔算子和普瑞维特算子)和二阶梯度算子(拉普拉斯算子)进行边缘提取。
clc;clear;close all;
path(path,'D:\R2019a\toolbox\images\imdata');
%读取原始图像
I=imread('lighthouse.png');
I=rgb2gray(I);
I=double(I);
I=I/max(I(:));
subplot(2,3,1);imshow(I,[0,1]);title('ground truth');
%罗伯特算子
robertsBW=RobertsOperator(I);
robertsBW=robertsBW/max(robertsBW(:));
subplot(2,3,2);imshow(robertsBW,[0,1]);title('Roberts');
%索贝尔算子
sobelBW=SobelOperator(I);
sobelBW=sobelBW/max(sobelBW(:));
subplot(2,3,3);imshow(sobelBW,[0,1]);title('Sobel');
%普瑞维特算子
prewittBW=PrewittOperator(I);
prewittBW=prewittBW/max(prewittBW(:));
subplot(2,3,4);imshow(prewittBW,[0,1]);title('Prewitt');
%拉普拉斯算子
logBW=LaplaceOperator(I);
logBW=logBW/max(logBW(:));
subplot(2,3,5);imshow(logBW,[0,1]);title('Laplace');
%不同算子边缘检测具体函数实现:
function [edge]= RobertsOperator(pic)
edge = zeros(size(pic));
h = size(pic, 1);
w = size(pic, 2);
for i = 1 : h - 1
for j = 1 : w - 1
edge(i, j) =abs(pic(i, j) - pic(i + 1, j + 1)) + abs(pic(i, j + 1) - pic(i + 1, j));
end
end
end
function [edge] = SobelOperator(pic)
edge = zeros(size(pic));
h = size(pic, 1);
w = size(pic, 2);
gx = [-1, -2, -1; 0, 0, 0; 1, 2, 1];
gy = gx';
for i = 2 : h - 1
for j = 2 : w - 1
sub = double(pic(i - 1 : i + 1, j - 1 : j + 1));
g1 = abs(sum(sum(sub .* gx)));
g2 = abs(sum(sum(sub .* gy)));
if g1 > g2
edge(i, j) = g1;
else
edge(i, j) = g2;
end
end
end
end
function [edge] = PrewittOperator(pic)
edge = zeros(size(pic));
h = size(pic, 1);
w = size(pic, 2);
gx = [-1, -1, -1; 0, 0, 0; 1, 1, 1];
gy = gx';
for i = 2 : h - 1
for j = 2 : w - 1
sub = double(pic(i - 1 : i + 1, j - 1 : j + 1));
g1 = abs(sum(sum(sub .* gx)));
g2 = abs(sum(sum(sub .* gy)));
if g1 > g2
edge(i, j) = g1;
else
edge(i, j) = g2;
end
end
end
end
function [edge] = LaplaceOperator(pic)
edge =zeros(size(pic));
h = size(pic, 1);
w = size(pic, 2);
l = [0, 1, 0; 1, -4, 1; 0, 1, 0];
for i = 2 : h - 1
for j = 2 : w - 1
sub = double(pic(i - 1 : i + 1, j - 1 : j + 1));
d = sum(sum(sub .*l));
edge(i, j) =d;
end
end
end
- 调出罗伯特算子和拉普拉斯算子函数,对相应的代码进行分析。
(1) 罗伯特算子函数核心源码分析:
function [edge]= RobertsOperator(pic)
edge = zeros(size(pic));%初始化边缘矩阵
h = size(pic, 1); %图片行数
w = size(pic, 2);%图片列数
%利用局部差分计算梯度算子,即对角方向相邻两像素值之差。
for i = 1 : h - 1
for j = 1 : w - 1
edge(i, j) =abs(pic(i, j) - pic(i + 1, j + 1)) + abs(pic(i, j + 1) - pic(i + 1, j));
end
end
end
(2) 拉普拉斯算子函数核心源码分析:
function [edge] = LaplaceOperator(pic)
edge =zeros(size(pic)); %初始化边缘矩阵
h = size(pic, 1); %图片行数
w = size(pic, 2); %图片列数
l = [0, 1, 0; 1, -4, 1; 0, 1, 0];% 拉普拉斯算子模板矩阵
for i = 2 : h - 1
for j = 2 : w - 1
sub = double(pic(i - 1 : i + 1, j - 1 : j + 1));
d = sum(sum(sub .*l));%卷积求和运算
edge(i, j) =d;%更新边缘矩阵
end
end
end
4.3 实验结果
对原图像分别用一阶罗伯特算子、索贝尔算子和普瑞维特算子以及二阶拉普拉斯算子处理,得到的实验图像如下所示:

由实验效果图可以看出不同的梯度算子对原图像进行边缘提取的效果不同。其中,罗伯特算子采用的是对角方向相邻像素值之差,定位比较精准。索贝尔算子对灰度渐变和噪声较多的图像处理效果较好,采用的是加权平均再进行微分运算的方法。普瑞维特算子是利用局部差分平均方法寻找边缘,效果和索贝尔算子接近。拉普拉斯算子是一种二阶导数算子,对噪声更敏感,能对任何走向的界线和线条进行锐化,无方向性。因此一般用于判断边缘像素相对图像的明暗程度,不直接用于边缘检测。