《深度学习》之 卷积神经网络 详解
卷积神经网络
一.概括
1.1为什么要出现卷积神经网络?
全连接神经网络出现的维度灾难,内存计算量巨大,训练困难

(图片来自网络)
什么是卷积神经网络?
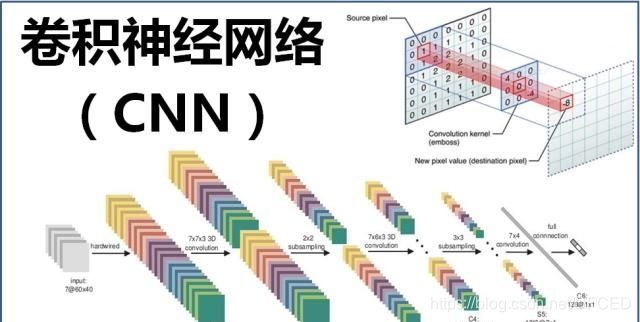
卷积神经网络(Convolutional Neural Networks / CNNs / ConvNets)与普通神经网络非常相似,它们都由具有可学习的权重和偏置常量(biases)的神经元组成。每个神经元都接收一些输入,并做一些点积计算,输出是每个分类的分数,普通神经网络里的一些计算技巧到这里依旧适用。
所以哪里不同呢?卷积神经网络默认输入是图像,可以让我们把特定的性质编码入网络结构,使是我们的前馈函数更加有效率,并减少了大量参数。
(图片来自网络)
二.什么是感受野
2.1 感受野的概念
生理学上
感受野,感受器受刺激兴奋时,通过感受器官中的向心神经元将神经冲动(各种感觉信息)传到上位中枢,一个神经元所反应(支配)的刺激区域就叫做神经元的感受野(receptive field)。又译为受纳野。末梢感觉神经元、中继核神经元以及大脑皮层感觉区的神经元都有各自的感受野。随感觉种类不同,感受野的性质、大小也不一致。
在视觉通路上,视网膜上的光感受器(杆体细胞和锥体细胞)通过接受光并将它转换为输出神经信号而来影响许多神经节细胞,外膝状体细胞以及视觉皮层中的神经细胞。反过来,任何一种神经细胞(除起支持和营养作用的神经胶质细胞外)的输出都依赖于视网膜上的许多光感受器。我们称直接或间接影响某一特定神经细胞的光感受器细胞的全体为该特定神经细胞的感受野(receptive field)。
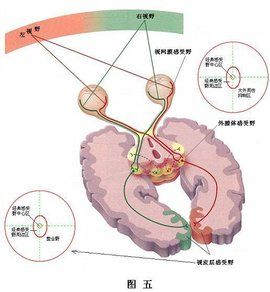
(图片来自网络)
卷积网络中
在卷积神经网络中,感受野(Receptive Field)的定义是卷积神经网络每一层输出的特征图(feature map)上的像素点在输入图片上映射的区域大小。再通俗点的解释是,特征图上的一个点对应输入图上的区域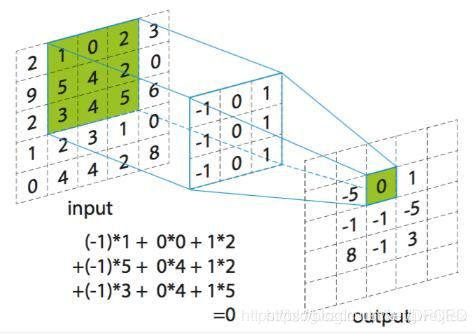
(图片来自网络)
三. 什么是卷积?
在泛函分析中,卷积、旋积或摺积(英语:Convolution)是通过两个函数f 和g 生成第三个函数的一种数学算子,表征函数f 与g经过翻转和平移的重叠部分函数值乘积对重叠长度的积分。
如果将参加卷积的一个函数看作区间的指示函数,卷积还可以被看作是“滑动平均”的推广。
连续值的卷积公式:
![]()
离散型的卷积公式:
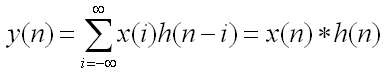
如图所示,卷积可以保留原有特征,和压缩维度

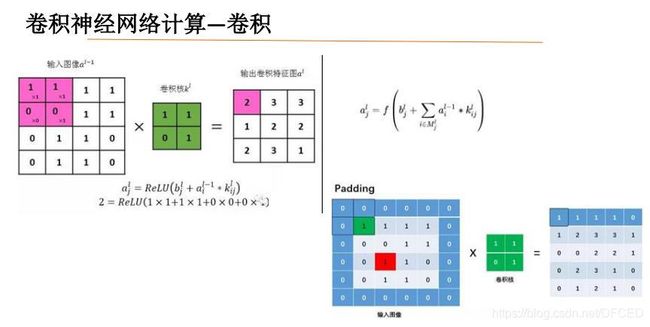
(图片来自网络)
四.图像的编码
4.1 概念
图像编码就是对将要处理的图像源数据按照一定的规则进行变换和组合,从而使得可以用尽可能少的符号来表示尽可能多的信息。源图像中常常存在各种各样的冗余:空间冗余、时间冗余、信息熵冗余、结构冗余、知识冗余等,这就使得通过编码来进行压缩成为了可能。
4.2 分类
根据压缩效果
**1. 有损编码:**有损编码在编码的过程中把不相干的信息都删除了,只能对原图像进行近似的重建
2. 无损编码:
无损编码的压缩算法中赶紧进删除了图像数据中的冗余信息,解压缩时能够精确恢复原图像。
根据编码原理:
1. 预测编码:
预测编码是利用图像信号在局部空间和时间范围内的高度相关性,以已经传出的近邻像素值作为参考,预测当前像素值,然后量化、编码预测误差。预测编码广泛应用于运动图像、视频编码如数字电视、视频电话中。
2.变换编码
变换编码利用正交变换将图像从空域映射到另一个域上使得变换后的系数之间相关性降低,其变换并无压缩性,但可以结合其他编码方式进行压缩。
3.统计编码:
统计编码也称为熵编码,它是一类根据信息熵原理进行的信息保持型变字长编码。编码时对出现概率高的事件(被编码的符号)用短码表示,对出现概率低的事件用长码表示。常见的熵编码有哈弗曼编码、算术编码和行程编码。
五.池化
在卷积神经网络中,我们经常会碰到池化操作,而池化层往往在卷积层后面,通过池化来降低卷积层输出的特征向量,同时改善结果(不易出现过拟合)。
为什么可以通过降低维度呢?
因为图像具有一种“静态性”的属性,这也就意味着在一个图像区域有用的特征极有可能在另一个区域同样适用。因此,为了描述大的图像,一个很自然的想法就是对不同位置的特征进行聚合统计,例如,人们可以计算图像一个区域上的某个特定特征的平均值 (或最大值)来代表这个区域的特征。[1]
5.1 一般池化
最常见的池化操作为平均池化mean pooling和最大池化max pooling:
平均池化:计算图像区域的平均值作为该区域池化后的值。
最大池化:选图像区域的最大值作为该区域池化后的值。

(图片来自网络)
2. 重叠池化(OverlappingPooling)
重叠池化正如其名字所说的,相邻池化窗口之间会有重叠区域,此时sizeX>stride。
其他的设置都不变的情况下, top-1和top-5 的错误率分别减少了0.4% 和0.3%。
3. 空金字塔池化(Spatial Pyramid Pooling)
空间金字塔池化可以把任何尺度的图像的卷积特征转化成相同维度,这不仅可以让CNN处理任意尺度的图像,还能避免cropping和warping操作,导致一些信息的丢失,具有非常重要的意义。
一般的CNN都需要输入图像的大小是固定的,这是因为全连接层的输入需要固定输入维度,但在卷积操作是没有对图像尺度有限制,所有作者提出了空间金字塔池化,先让图像进行卷积操作,然后转化成维度相同的特征输入到全连接层,这个可以把CNN扩展到任意大小的图像。
4.对全局平均池化(GAP)
所谓的全局就是针对常用的平均池化而言,平均池化会有它的filter size,比如 2 * 2,全局平均池化就没有size,它针对的是整张feature map.
5.池化的作用
池化操作后的结果相比其输入缩小了。池化层的引入是仿照人的视觉系统对视觉输入对象进行降维和抽象。在卷积神经网络过去的工作中,研究者普遍认为池化层有如下三个功效:
1.特征不变:池化操作是模型更加关注是否存在某些特征而不是特征具体的位置。
2.特征降维:池化相当于在空间范围内做了维度约减,从而使模型可以抽取更加广范围的特征。同时减小了下一层的输入大小,进而减少计算量和参数个数。
3.在一定程度上防止过拟合,更方便优化。
六.LeNet框架
LeNet-5是一个较简单的卷积神经网络。下图显示了其结构:输入的二维图像,先经过两次卷积层到池化层,再经过全连接层,最后使用softmax分类作为输出层。

(图片来自网络)
LeNet-5 这个网络虽然很小,但是它包含了深度学习的基本模块:卷积层,池化层,全连接层。是其他深度学习模型的基础, 这里我们对LeNet-5进行深入分析。同时,通过实例分析,加深对与卷积层和池化层的理解。

LeNet-5共有7层,不包含输入,每层都包含可训练参数;每个层有多个Feature Map,每个FeatureMap通过一种卷积滤波器提取输入的一种特征,然后每个FeatureMap有多个神经元。
参考:
《深度学习》花书
复旦大学 《深度学习》
