基于最小二乘支持向量机(LS-SVM)进行分类、函数估计、时间序列预测和无监督学习(Matlab代码实现)
欢迎来到本博客❤️❤️
博主优势:博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
目录
1 概述
2 运行结果
3 参考文献
4 Matlab代码及详细文章阅读
1 概述
很多力学、工程等学科中的问题都可以归结为积分方程,例如电磁问题、位势问题1。近年来,无论在理论上[31.,还是在数值解法上[4),对积分方程的研究都取得了丰硕的成果。就数值解而言,一些新方法被不断推出,但该方法的两个缺点(隐含层数难确定、容易陷入局部极小值)对克服第一类积分方程的不适定性不利。最小二乘支持向量机(least squares support vector machine,LS-SVM)能较好地克服这两个缺点,并已成功地应用于解微分方程及其反问题。LS-SVM作为一种机器学习方法,本文基于最小二乘支持向量机(LS-SVM)进行分类、函数估计、时间序列预测和无监督学习。
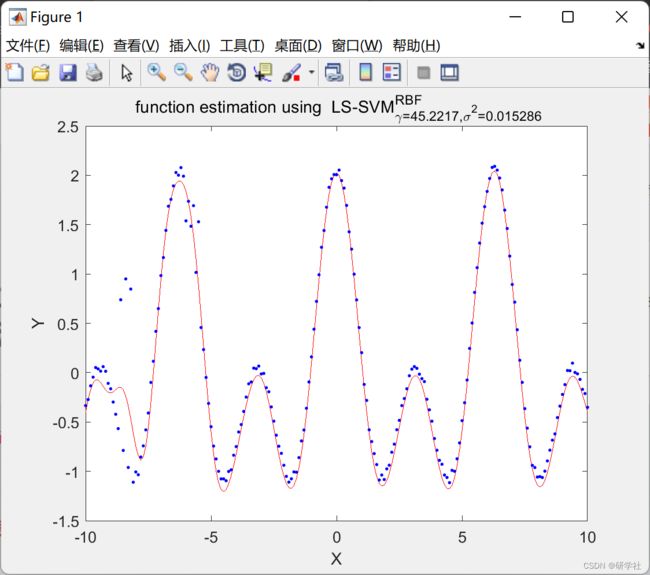
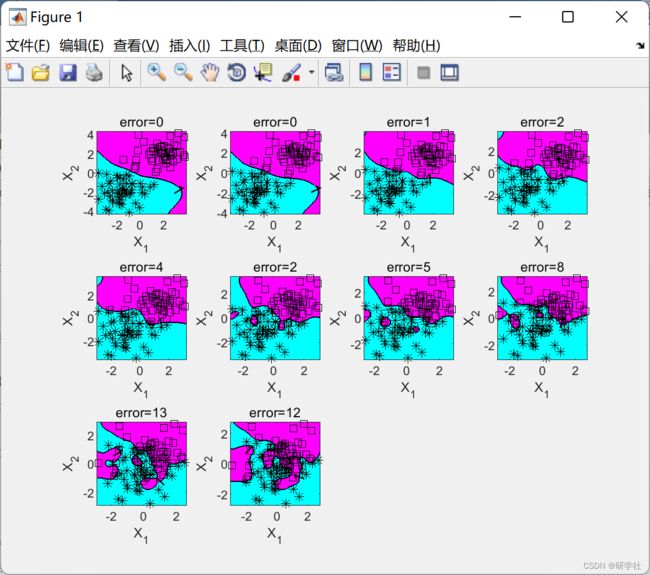
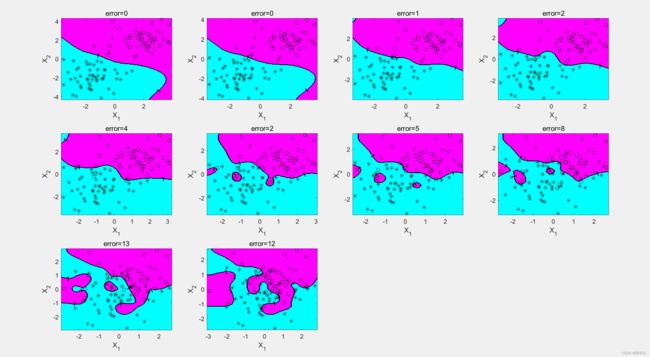
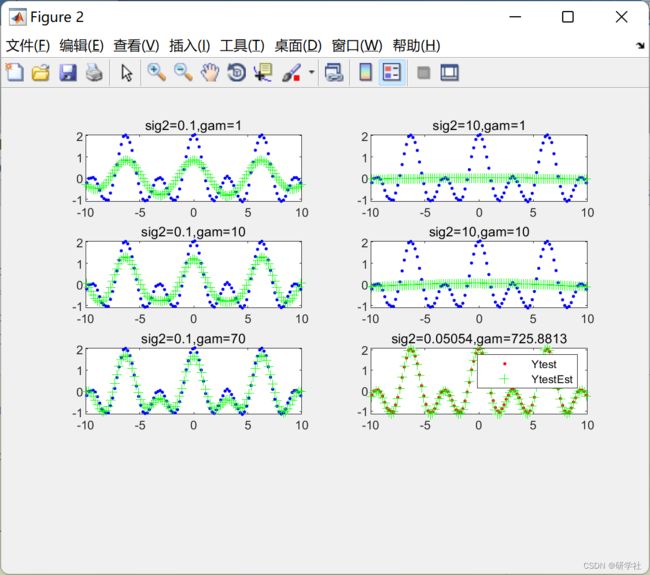
2 运行结果
篇幅原因,展现部分运行结果:
部分代码:
randn('state',100)
X1 = +1 + randn(50,2);
randn('state',200);
X2 = -1 + randn(51,2);
X = [X1; X2];
Y1 = ones(size(X1,1),1);
Y2 = -1*ones(size(X2,1),1);
Y = [Y1; Y2];
%test data
x = -5.0:0.25:5.0;
y = -5.0:0.25:5.0;
[xt, yt] = meshgrid(x,y);
grid = [xt(:) yt(:)];
%bayes classifier
% pc1 = normpdf2(grid, [-1; -1], [1 0;0 1]);
% pc2 = normpdf2(grid, [+1; +1], [1 0;0 1]);
% class = pc1>=pc2;
%estimate bayes classfier
mean1 = mean(X1); mean2 = mean(X2);
cov1 = cov(X1); cov2 = cov(X2);
pc1 = normpdf2(grid, mean2, cov2);
pc2 = normpdf2(grid, mean1, cov1);
class = pc1>=pc2;
%visualization
grid = reshape(class,length(x),length(y));
contourf(x,y,grid,2);hold on;
hold on
plot(X1(:,1),X1(:,2),'ro');
plot(X2(:,1),X2(:,2),'bo');
title('Plot of Samples');
%legend([pos neg],'positive data','negative data');
hold off
X=(-10:0.1:10)';
Y = cos(X) + cos(2*X) + 0.1.*rand(length(X),1);
out=[15 17 19];
Y(out)=0.7+0.3*rand(size(out));
out=[41 44 46];
Y(out)=1.5+0.2*rand(size(out));
gam=100;sig2=0.1;
[alpha,b]=trainlssvm({X,Y,'f',gam,sig2,'RBF_kernel'});
plotlssvm({X,Y,'f',gam,sig2,'RBF_kernel'},{alpha,b});
%%
model=initlssvm(X,Y,'f',[],[],'RBF_kernel');
costFun='rcrossvalidatelssvm';
wFun='whuber';
model=tunelssvm(model,'simplex',costFun,{10,'mae'},wFun);
model=robustlssvm(model);
plotlssvm(model);
3 参考文献
[1]苏磊·乃比,张辉国,胡锡健.基于LS-SVM的时空变系数回归模型算法及仿真[J].计算机仿真,2022,39(07):342-347.
[1]曹秀梅,朱明月,吴自库.基于LS-SVM的第一类积分方程的近似解法[J].青岛农业大学学报(自然科学版),2022,39(03):222-225.