非线性海洋捕食者算法（Matlab代码实现）

 ‍个人主页：研学社的博客 

欢迎来到本博客❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

本文目录如下：

目录

1 概述

2 运行结果

3 参考文献

4 Matlab代码实现

---

1 概述

NMPA是一项有影响力的尝试，旨在识别和缓解最近提出的称为海洋捕食者算法（MPA）的优化技术的一些问题。通过对其探索性和剥削行为的视觉调查，可以观察到搜索从全局到本地的转变可以进一步改善。作为一种极具成本效益的方法，使用一组非线性函数来改变MPA算法的搜索模式。所提出的算法称为非线性马林捕食者算法（NMPA），在一组基准函数上进行了测试。一项全面的比较研究表明，与原始的MPA甚至其他最近的元启发式方法相比，所提出的方法具有优越性。本文还考虑围绕超越5G（B5G）网络的非正交多址（NOMA）和可见光通信（VLC）中的功率分配进行实际案例研究，以展示NMPA算法的适用性。与最先进的算法相比，NMPA算法在解决广泛的基准功能以及为NOMA-VLC-B5G系统中的多个用户获得公平的功率分配方面显示出其优越性。

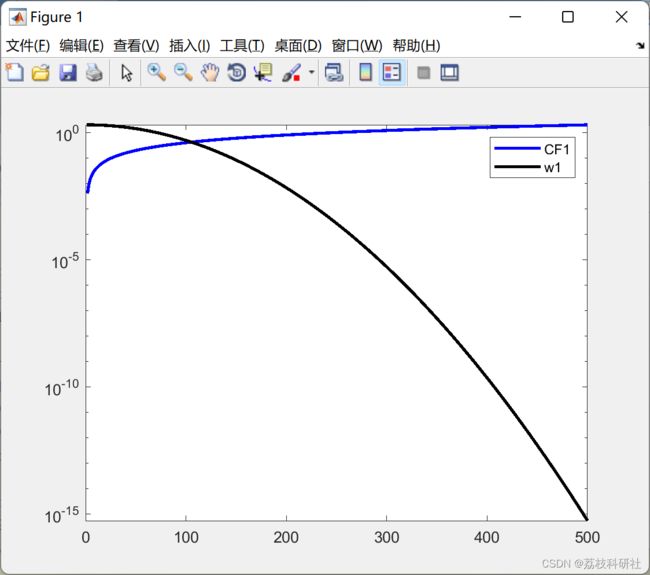
2 运行结果

部分代码：

 % % function topology
% figure('Position',[500 400 700 290])
% subplot(1,2,1);
% figure;
% func_plot(Function_name);
% title('Func.13')
% xlabel('x_1');
% ylabel('x_2');
% zlabel([Function_name,'( x_1 , x_2 )'])
% 
% Convergence curve
% subplot(1,2,2);
% semilogy(Convergence_curve,'Color','r','Linewidth',2)
% hold on
% semilogy(Convergence_curve1,'Color','k','Linewidth',2)
% hold on
% semilogy(MVO_Convergence_curve,'Color','b','Linewidth',2)
% hold on
% semilogy(MFO_Convergence_curve,'Color',[1.000000000000000                   0                   0],'Linewidth',2)
% hold on
% semilogy(SSA_Convergence_curve,'Color',[0.800000000000000   1.000000000000000                   0],'Linewidth',2)
% hold on
% semilogy(GWO_Convergence_curve,'Color',[0   1.000000000000000   0.400000000000000],'Linewidth',2)
% hold on
% semilogy(PSO_cg_curve,'Color',[0   0.400000000000000   1.000000000000000],'Linewidth',2)
% hold on
% semilogy(de_BestCost,'Color',[0.800000000000001                   0   1.000000000000000],'Linewidth',2)
% title('Objective space')
% xlabel('Iteration');
% ylabel('Best score obtained so far');
% legend('MPA','NMPA','MVO','MFO','SSA','GWO','PSO','DE');
% 
% 
% display(['The best solution obtained by MPA is : ', num2str(Best_pos,10)]);
% display(['The best optimal value of the objective function found by MPA is : ', num2str(Best_score,10)]);
% disp(sprintf('--------------------------------------'));

function [Top_predator_fit,Top_predator_pos,Convergence_curve,T]=MPA(SearchAgents_no,Max_iter,lb,ub,dim,fobj)
tic;

Top_predator_pos=zeros(1,dim);
Top_predator_fit=inf; 

Convergence_curve=zeros(1,Max_iter);
stepsize=zeros(SearchAgents_no,dim);
fitness=inf(SearchAgents_no,1);

Prey=initialization(SearchAgents_no,dim,ub,lb);
  
Xmin=repmat(ones(1,dim).*lb,SearchAgents_no,1);
Xmax=repmat(ones(1,dim).*ub,SearchAgents_no,1);
         

Iter=0;
FADs=0.2;
P=0.5;

while Iter      %------------------- Detecting top predator -----------------    
 for i=1:size(Prey,1)  
        
    Flag4ub=Prey(i,:)>ub;
    Flag4lb=Prey(i,:)     Prey(i,:)=(Prey(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;                    
        
    fitness(i,1)=fobj(Prey(i,:));
                     
     if fitness(i,1)        Top_predator_fit=fitness(i,1); 
       Top_predator_pos=Prey(i,:);
     end          
 end
     
     %------------------- Marine Memory saving ------------------- 
    
 if Iter==0
   fit_old=fitness;    Prey_old=Prey;
 end
     
  Inx=(fit_old   Indx=repmat(Inx,1,dim);
  Prey=Indx.*Prey_old+~Indx.*Prey;
  fitness=Inx.*fit_old+~Inx.*fitness;
        
  fit_old=fitness;    Prey_old=Prey;

     %------------------------------------------------------------   
     
 Elite=repmat(Top_predator_pos,SearchAgents_no,1);  %(Eq. 10) 
 CF=(1-Iter/Max_iter)^(2*Iter/Max_iter);
                             
 RL=0.05*levy(SearchAgents_no,dim,1.5);   %Levy random number vector
 RB=randn(SearchAgents_no,dim);          %Brownian random number vector
           
  for i=1:size(Prey,1)
     for j=1:size(Prey,2)        
       R=rand();
          %------------------ Phase 1 (Eq.12) ------------------- 
       if Iter           stepsize(i,j)=RB(i,j)*(Elite(i,j)-RB(i,j)*Prey(i,j));                    
          Prey(i,j)=Prey(i,j)+P*R*stepsize(i,j); 
             
          %--------------- Phase 2 (Eqs. 13 & 14)----------------
       elseif Iter>Max_iter/3 && Iter<2*Max_iter/3 
          
         if i>size(Prey,1)/2
            stepsize(i,j)=RB(i,j)*(RB(i,j)*Elite(i,j)-Prey(i,j));
            Prey(i,j)=Elite(i,j)+P*CF*stepsize(i,j); 
         else
            stepsize(i,j)=RL(i,j)*(Elite(i,j)-RL(i,j)*Prey(i,j));                     
            Prey(i,j)=Prey(i,j)+P*R*stepsize(i,j);  
         end  
         
         %----------------- Phase 3 (Eq. 15)-------------------
       else 
           
           stepsize(i,j)=RL(i,j)*(RL(i,j)*Elite(i,j)-Prey(i,j)); 
           Prey(i,j)=Elite(i,j)+P*CF*stepsize(i,j);  
    
       end  
      end                                         
  end    
        
     %------------------ Detecting top predator ------------------        
  for i=1:size(Prey,1)  
        
    Flag4ub=Prey(i,:)>ub;  
    Flag4lb=Prey(i,:)     Prey(i,:)=(Prey(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
  
    fitness(i,1)=fobj(Prey(i,:));
        
      if fitness(i,1)          Top_predator_fit=fitness(i,1);
         Top_predator_pos=Prey(i,:);
      end     
  end
        
     %---------------------- Marine Memory saving ----------------
    
 if Iter==0
    fit_old=fitness;    Prey_old=Prey;
 end
     
    Inx=(fit_old     Indx=repmat(Inx,1,dim);
    Prey=Indx.*Prey_old+~Indx.*Prey;
    fitness=Inx.*fit_old+~Inx.*fitness;

3 参考文献

部分理论来源于网络，如有侵权请联系删除。

Sadiq, Ali Safaa, et al. “Nonlinear Marine Predator Algorithm: A Cost-Effective Optimizer for Fair Power Allocation in NOMA-VLC-B5G Networks.” Expert Systems with Applications, Elsevier BV, May 2022, p. 117395, doi:10.1016/j.eswa.2022.117395.

4 Matlab代码实现