cs224w（图机器学习）2021冬季课程学习笔记5 Colab 1：Node Embeddings

诸神缄默不语-个人CSDN博文目录
cs224w（图机器学习）2021冬季课程学习笔记集合

VX号“PolarisRisingWar”可直接搜索添加作者好友讨论。

colab 1 文件原始下载地址

我将写完的colab 1文件发到了GitHub上，有一些个人做笔记的内容。地址：cs224w-2021-winter-colab/CS224W_Colab_1.ipynb at master · PolarisRisingWar/cs224w-2021-winter-colab

---

本colab以无向图 Karate Club Network¹ （有34个节点，78条边）为例，探索该数据集的相关统计量，并将从NetworkX下载的数据集转换为PyTorch的Tensor格式，用边连接作为节点相似性度量指标实现shallow encoder（以 nn.Embedding 为embedding-lookup）的节点嵌入代码。

节点嵌入训练概览：
用图中原本的边作为正值，从不存在的边中抽样作为负值，将对应边/节点对的点积结果用sigmoid归一化后视作输出值，将1视为正值的标签，0视为负值的标签。用BCELoss计算损失函数。
将nn.Embedding作为参数，用PyTorch在神经网络中以随机梯度下降的方式进行训练。
最后通过PCA将nn.Embedding.weight（即embedding-lookup的值）降维到二维上，通过可视化的方式直观检验训练效果。

0. Python包导入

import networkx as nx

import torch
import torch.nn as nn
from torch.optim import SGD

import matplotlib.pyplot as plt

from sklearn.decomposition import PCA

import random

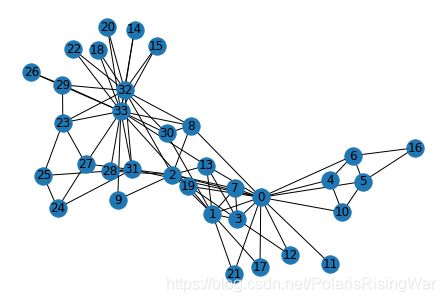
1. NetworkX数据获取、可视化

数据获取：

G = nx.karate_club_graph()
print(type(G))

可视化：

nx.draw(G, with_labels = True)

2. 探索NetworkX数据的相关统计量

2.1 求平均度数，保留到整数

平均度数=2E/N

num_edges = G.number_of_edges()
num_nodes = G.number_of_nodes()
avg_degree=round(2*num_edges/num_nodes)

2.2 求平均clustering coefficient²，保留2位小数

avg_cluster_coef=round(nx.average_clustering(G),2)

2.3 求一次迭代后节点0的PageRank，保留2位小数（禁止使用nx.pagerank）

PageRank公式：$r_j={\sum }_{i\to j}\beta \frac{r_i}{d_i}+(1-\beta )\frac{1}{N}$

beta = 0.8

r0 = 1 / G.number_of_nodes()

#得到node0的邻居
#得到这些邻居的出度（是无向图，所以就是度数）
#计算得到右式中的第一项（\sum{i→j}\beta\frac{r_i}{d_i}）
#计算得到r_j
for ni in nx.neighbors(G,0):
   #得到的每一个ni都是node0邻居的索引
   di=G.degree[ni]  #获取node_ni的度数
   r1+=beta*r0/di
r1+=(1-beta)*(1/G.number_of_nodes())
r1=round(r1,2)

2.4 计算节点5的 (raw) closeness centrality²，保留2位小数

closeness centrality公式：$c(v)=\frac{1}{{\sum }_{u\ne v}\text{shortest path length between }u\text{ and }v}$


解法1：不使用NetworkX内置的closeness centrality方法

node_length_pairs=nx.shortest_path_length(G,source=5)
#返回字典，key是节点索引，value是source与该节点间的最短路径长度

denominator=0  #分母
for i in range(G.number_of_nodes()):
  if i!=5:  #其实不用这个判断也行，如果i=5就会是0
    denominator+=node_length_pairs[i]
closeness=round(1/denominator,2)

解法2：使用NetworkX内置的closeness centrality方法
参考官方文档networkx.algorithms.centrality.closeness_centrality — NetworkX 2.5 documentation，这个函数是原始closeness centrality做了规范化（乘以 (图节点数量-1) ）

closeness=nx.closeness_centrality(G,u=5)
closeness=closeness/(G.number_of_nodes()-1)
closeness=round(closeness,2)

3. 将NetworkX Graph转换为PyTorch³ Tensor，得到可用于神经网络训练的输入数据

3.1 获取数据的edge list并将其转换为torch.LongTensor，得到作为正值的边

这里的edge list指的是一个元素为tuple的list，每个tuple的元素是两个节点，代表一条边连接这两个节点。
edge_index是尺寸为 [2, len(edge_list)] 的LongTensor。也就相当于是每列代表一条边。

根据函数计算出的pos_edge_index就是图中真实存在的边，作为正值。

def graph_to_edge_list(G):
  edge_list = []
  for edge in G.edges():
    edge_list.append(edge)
  return edge_list

def edge_list_to_tensor(edge_list):
  edge_index=torch.LongTensor(edge_list).t()
  return edge_index

pos_edge_list = graph_to_edge_list(G)
pos_edge_index = edge_list_to_tensor(pos_edge_list)

3.2 抽样得到作为负值的边，并判断边1-5能不能作为负边

根据题意，从图中抽样一定数目不存在的边，可以作为满足要求的负边。

最后得到的 neg_edge_index 也是尺寸为 [2, len(edge_list)] 的LongTensor。

def sample_negative_edges(G, num_neg_samples):
  #题目要求：不用考虑num_neg_samples比所有不存在边的数量还高的边界条件
  #不考虑自环
  #注意，本来需要考虑逆边的问题，但是由于我采用的nx.non_edges函数不会出现两次重复节点对，所以不用考虑这个问题。

  neg_edge_list = []

  #得到图中所有不存在的边（这个函数只会返回一侧，不会出现逆边）
  non_edges_one_side=list(enumerate(nx.non_edges(G)))
  neg_edge_list_indices=random.sample(range(0,len(non_edges_one_side)),num_neg_samples)
  #取样num_neg_samples长度的索引
  for i in neg_edge_list_indices:
    neg_edge_list.append(non_edges_one_side[i][1])
  
  return neg_edge_list


# Sample 78 negative edges
neg_edge_list = sample_negative_edges(G, len(pos_edge_list))

# Transform the negative edge list to tensor
neg_edge_index = edge_list_to_tensor(neg_edge_list)

# Which of following edges can be negative ones?
edge_1 = (7, 1)
edge_2 = (1, 33)
edge_3 = (33, 22)
edge_4 = (0, 4)
edge_5 = (4, 2)

############# Your code here ############
#如果边在图中，就认为不行
print('edge_1'+(" can't" if G.has_edge(edge_1[0],edge_1[1]) else ' can')+' be negative edge')
print('edge_2'+(" can't" if G.has_edge(edge_2[0],edge_2[1]) else ' can')+' be negative edge')
print('edge_3'+(" can't" if G.has_edge(edge_3[0],edge_3[1]) else ' can')+' be negative edge')
print('edge_4'+(" can't" if G.has_edge(edge_4[0],edge_4[1]) else ' can')+' be negative edge')
print('edge_5'+(" can't" if G.has_edge(edge_5[0],edge_5[1]) else ' can')+' be negative edge')
#########################################

edge_1 can’t be negative edge
edge_2 can be negative edge
edge_3 can’t be negative edge
edge_4 can’t be negative edge
edge_5 can be negative edge

4. Node Emebedding Learning

建立一个节点嵌入模型。

4.1 初始化 nn.Embedding

Embedding类的官方文档：Embedding — PyTorch 1.8.1 documentation

nn.Embedding 可看作一个embedding词典，相当于一个shallow encoder的lookup，一个大矩阵。每一行存储一个item（在这里就是node）对应的embedding。
weight是这个矩阵的值（Tensor），weight.data可以改变该值。weight尺寸为 (num_embeddings, embedding_dim) ，从 $\mathcal{N}(0,1)$ 中初始化数据。
输入是索引的列表（IntTensor或LongTensor），输出是对应的词嵌入（也就是 emb.weight.data 中对应索引的表示向量）（尺寸为 (input尺寸,embedding_dim) ）。
num_embeddings是词典长度（int）。在这里就是指有多少个节点，因为我们要输入节点索引返回对应的embedding。
embedding_dim是表示向量维度（int）。

torch.manual_seed(1)

def create_node_emb(num_node=34, embedding_dim=16):
  #题目要求：用均匀分布初始化Embedding
  #其实我看了下文档，Embedding初始化本来就是均匀分布。不过在这里应该是要用manual_seed来维持可复现性
  emb=nn.Embedding(num_node,embedding_dim)
  emb.weight.data=torch.rand(num_node,embedding_dim)
  return emb

emb = create_node_emb()

4.2 可视化初始Embedding

首先建立以nn.Embedding为入参的可视化函数visualize_emb：将Embedding用PCA降维到二维，再将两类节点的嵌入的二维表示分别以红色和蓝色画出点。
在4.1中初始化的emb上应用visualize_emb函数。

def visualize_emb(emb):
  X = emb.weight.data.numpy()
  pca = PCA(n_components=2)
  components = pca.fit_transform(X)
  plt.figure(figsize=(6, 6))
  club1_x = []
  club1_y = []
  club2_x = []
  club2_y = []
  for node in G.nodes(data=True):
    if node[1]['club'] == 'Mr. Hi':
    #node的形式：第一个元素是索引，第二个元素是attributes字典
      club1_x.append(components[node[0]][0])
      club1_y.append(components[node[0]][1])
      #这里添加的元素就是节点对应的embedding经PCA后的两个维度
    else:
      club2_x.append(components[node[0]][0])
      club2_y.append(components[node[0]][1])
  plt.scatter(club1_x, club1_y, color="red", label="Mr. Hi")
  plt.scatter(club2_x, club2_y, color="blue", label="Officer")
  plt.legend()
  plt.show()

# Visualize the initial random embeddding
visualize_emb(emb)

可以看到两种节点分布得很散乱，说明初始化得很随便：

4.3 训练Embedding

训练目标：使有边连接（pos_edge_index）的节点嵌入点乘结果趋近于1，无边连接的趋近于0。

def accuracy(pred, label):
  #题目要求：
  #输入参数：
  #  pred (the resulting tensor after sigmoid)
  #  label (torch.LongTensor)
  #预测值大于0.5被分类为1，否则就为0
  #准确率返回值保留4位小数
  
  #accuracy=预测与实际一致的结果数/所有结果数
  #pred和label都是[78*2=156]大小的Tensor
  accu=round(((pred>0.5)==label).sum().item()/(pred.shape[0]),4)
  return accu


def train(emb, loss_fn, sigmoid, train_label, train_edge):
  #题目要求：
  #用train_edge中的节点获取节点嵌入
  #点乘每一点对的嵌入，将结果输入sigmoid
  #将sigmoid输出输入loss_fn
  #打印每一轮的loss和accuracy

  epochs = 500
  learning_rate = 0.1

  optimizer = SGD(emb.parameters(), lr=learning_rate, momentum=0.9)

  for i in range(epochs):
    optimizer.zero_grad()
    train_node_emb=emb(train_edge)  #[2,156,16]
    #156是总的用于训练的边数，指78个正边+78个负边
    dot_product_result=train_node_emb[0].mul(train_node_emb[1])  #点对之间对应位置嵌入相乘，[156,16]
    dot_product_result=torch.sum(dot_product_result,1)  #加起来，构成点对之间向量的点积，[156]
    sigmoid_result=sigmoid(dot_product_result)  #将这个点积结果经过激活函数映射到0,1之间
    loss_result=loss_fn(sigmoid_result,train_label)
    loss_result.backward()
    optimizer.step()
    if i%10==0:  #其实这个应该每一轮都打印一遍的，但是我嫌太大了就十轮打印一遍了
      print(loss_result)
      print(accuracy(sigmoid_result,train_label))


loss_fn = nn.BCELoss()
sigmoid = nn.Sigmoid()

# Generate the positive and negative labels
pos_label = torch.ones(pos_edge_index.shape[1], )
neg_label = torch.zeros(neg_edge_index.shape[1], )

# Concat positive and negative labels into one tensor
train_label = torch.cat([pos_label, neg_label], dim=0)

# Concat positive and negative edges into one tensor
# Since the network is very small, we do not split the edges into val/test sets
train_edge = torch.cat([pos_edge_index, neg_edge_index], dim=1)

train(emb, loss_fn, sigmoid, train_label, train_edge)

输出结果不赘。

4.4 可视化训练后的Embedding

visualize_emb(emb)

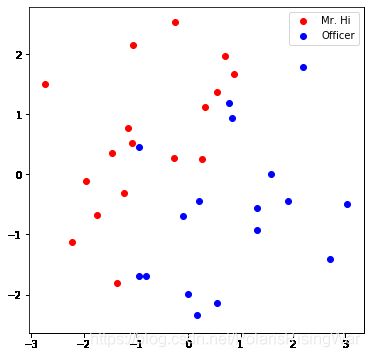
注意：我们没有用节点的club特征来训练，但是我们从数据集情况中知道根据图结构可以将节点按照club特征进行分类。因此，如果我们训练得到的节点嵌入可以将两类节点分得比较开，说明我们的表示向量确实抓住了相应的图结构信息，说明我们的节点嵌入是比较好的。

从图中可以发现两类还是分得很开的，这就说明我们的训练还挺有效的。

5. 文中未列出的其他参考资料

1. torch.nn.Embedding_越努力 越幸运-CSDN博客_torch.nn.embedding
2. pytorch中的embedding词向量的使用_david0611的博客-CSDN博客
3. 图神经网络（02）-基于Graph的传统机器学习方法 - Heywhale.com 写代码的时候参考了这个项目里的notebook。我记得好像这个notebook里面有问题，但是看代码好累，我觉得我自己的代码应该是对的了，我就懒得看别人的了。

---

1. 该数据集的详细介绍见：图数据集Zachary‘s karate club network详解，包括其在NetworkX、PyG上的获取和应用方式 ↩︎

2. 指标详解见我之前写的笔记：cs224w（图机器学习）2021冬季课程学习笔记2 2. Traditional Feature-based Methods: Node ↩︎ ↩︎

3. PyTorch入门可参考我之前写的笔记：60分钟闪击速成PyTorch（Deep Learning with PyTorch: A 60 Minute Blitz）学习笔记 ↩︎