神经网络算法介绍

引言

人工神经网络（Artificial Neural Networks，ANN）最早起源于1943年，受“脑神经元学说”的启发，心理学家W·Mcculloch和数理逻辑学家W·Pitts首次提出基于神经元的数学模型，后来经过无数人的改进和完善，一直发展至今，而这发展中间经历了多次低谷，主要原因是当时的计算机算力不足。在2000年左右，随着计算机技术的成熟，神经网络迎来了迅猛发展，现如今，深度学习（深度神经网络）已经应用于自动驾驶、人脸识别、语音助理、数据挖掘等多个领域，是支撑现代社会的一项核心技术。

模型的数学结构

人工神经网络模型的结构与动物大脑神经结构极为相似，它接收输入数据，计算处理后输出预测结果，本质上是一个预测器。举个例子，一个人看到一张苹果图片，说这是苹果，那么苹果图片就是输入数据，大脑处理后输出预测结果：这是苹果。

通常，人工神经网络模型由输入层、隐藏层、输出层组成，其中隐藏层可以为多层，多层隐藏层的神经网络又称深度神经网络。神经网络的每一层都有若干个神经元，层与层之间的神经元相互全连接，每一个神经元接收前一层神经元的输出值作为输入值，进行处理后输出到下一层神经元，最终输出层的神经元输出预测结果值。

上图展示了一个简易的神经网络模型，下面对它进行说明：

• ${\Theta }^j$：第$j$层到第$j+1$层神经元的参数（又叫权重值）组成的矩阵，加下标后表示矩阵中的具体值
• $a_i^{(j)}$：第$j$层第$i$个神经元的激活项（激活项：该神经元计算并输出的值）；对于隐藏层和输出层，每个神经元的输入值就是前一层神经元的全体输出值，对这些值进行函数运算后作为该神经元的输出值
• $g()$：神经元的激活函数，通常是$Sigmoid$函数

模型理解

对神经网络的单个神经元来讲，它内部的运算可以看成是一个逻辑回归（当激活函数是$Sigmoid$函数时），而我们知道逻辑回归可以处理简单的预测问题，因此，当这样多个逻辑回归互相嵌套，组成多层的复杂结构时，就可以对于特征数据的细微误差进行更精准的感知和判断，于是可以像人一样处理非常复杂的预测问题。

多元分类问题

如果输出层只有单个神经元，则只能进行二分类（Sigmoid逻辑函数，是或否），要进行多元分类，则需要输出层有更多的神经元。如下图，为了识别一个图像是下面四类中的哪一类：行人、小汽车、摩托车、卡车，神经网络的输出层有四个相应的单元，这样的输出结果将会是一个四维向量，向量的4个值分别判断是否属于该类别，从而进行多元分类。注意，多元分类的神经网络的输出层一般至少是3个单元，因为2个单元是进行二分类，而二分类只需要一个输出层单元就可以完成。

代价函数（Lost Function）

代价函数就是把每个样本的损失函数进行求和，而损失函数代表该样本的实际$y$值与预测$y$值之间的误差值。

神经网络的代价函数与逻辑回归的代价函数极为相似，区别在于神经网络的输出层一般是多个单元，可以看作是多个逻辑回归，因此计算中需要将每个单元的误差值求和。下面是其数学表达式及说明：
$$\begin{array}{rl}J(\Theta )=& -\frac{1}{m}\left[\sum _{i=1}^m\sum _{k=1}^K{y}_k^{(i)}\log {\left(h_{\Theta }\left(x^{(i)}\right)\right)}_k+\left(1-y_k^{(i)}\right)\log \left(1-{\left(h_{\Theta }\left(x^{(i)}\right)\right)}_k\right)\right]\\ & +\frac{\lambda }{2m}\sum _{l=1}^{L-1}\sum _{i=1}^{s_l}\sum _{j=1}^{s_{l+1}}{\left({\Theta }_{ji}^{(l)}\right)}^2\end{array}$$

• m：用于训练模型的样本总数
• K：输出层的单元数量
• i：第i个样本
• $h_{\Theta }(x)$：K维向量，表示输出层的K个预测函数
• ${\left(h_{\Theta }(x)\right)}_k$：K维向量的第k个元素
• $\frac{\lambda }{2m}{\sum }_{l=1}^{L-1}{\sum }_{i=1}^{s_l}{\sum }_{j=1}^{s_{l+1}}{\left({\Theta }_{ji}^{(l)}\right)}^2$：这个是用来防止过拟合的正则项，把每一层的每一个${\Theta }_{ji}^{(l)}$（参数，权重值）进行平方求和并在前面加一个系数。

反向传播算法（Backpropagation Algorithm）

神经网络的强大之处在于使用反向传播算法来求解代价函数的收敛问题，这在大规模学习中非常高效。

这里需要思考，为什么不直接使用代价函数对参数求导的梯度下降算法来更新参数呢？原因在于，神经网络的结构相当于多层逻辑回归嵌套，并且层与层之间的单元相互全连接，导致预测函数的完整表达式非常复杂，应用链式求导法则时运算量巨大。但是，其实还有另一种办法，那就是使用类似下面的式子进行近似求导：
$$\frac{\partial y}{\partial x}\approx \frac{f(x+\Delta x)-f(x)}{\Delta x}$$
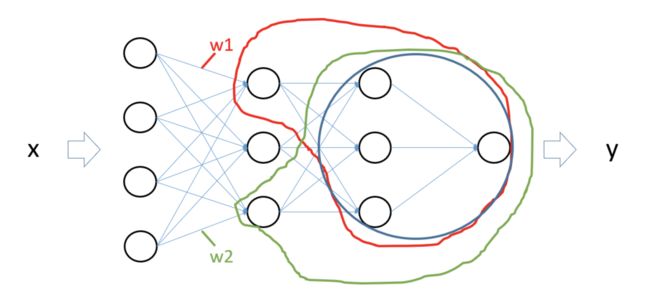
也就是要求某个参数的导数就让这个参数微变一点点，然后求出代价函数相对于参数变化量的比值。那么为何神经网络算法没有采用这种方法求导呢？我们来看下面图中的例子，现在假设输入向量经过正向传播后，现在要求出参数w1和w2的导数，按照上述方法计算时，对w1微扰后，需要重新计算红框内的节点；对w2微扰后，需要重新计算绿框内的节点。这两次计算中也有大量的“重复单元”即图中的蓝圈，实际上神经网络的每一个参数的计算都包含着这样大量的重复单元，那么神经网络规模一旦变大，这种算法的计算量一定爆炸，没有适用价值。

为了解决这些问题，早在1986年，Rumelhart、Hinton和Williams提出了反向传播算法。

反向传播算法利用了函数的链式求导法则，从输出层到输入层逐层计算模型参数的梯度值；同时它利用了动态规划思想，通过变换“计算方向”，避免了正向计算时的大量重复计算，这是因为应用链式求导法则时前面单元的偏导数是依赖于后面单元的，这样先计算后面的单元，再计算前面的单元就能利用后面单元的计算值，避免了重复计算，实现高效。同时，直观上也很好理解，因为神经网络的误差值其实是从后往前传播的，输入层就是样本数据的$x$，它的误差为0，输出层对应样本的$y$值，它是误差值的根源，模型的误差值从输出层开始层层向前面传播，这样逻辑上也符合反向传播算法的计算方式。

反向传播算法具体的步骤：

1、对训练集中的每一个样本$(x,y)$，进行正向计算：

第1层（输入层）：$a^{(1)}=x$

第2层：$z^{(2)}={\Theta }^{(1)}{a}^{(1)}$，$a^{(2)}=g\left(z^{(2)}\right))$

第3层：$z^{(3)}={\Theta }^{(2)}{a}^{(2)}$，$a^{(3)}=g\left(z^{(3)}\right))$

……

第L层（输出层）：$z^{(L)}={\Theta }^{(L-1)}{a}^{(L-1)}$，$a^{(L)}=h_{\Theta }(x)=g\left(z^{(L)}\right)$

2、在上一步的基础上，进行对误差值的反向计算：

（注：${\delta }^{(l)}$ 表示第 $l$ 层单元的误差值组成的向量, 全体单元误差值组成的矩阵记为 $△$, 矩阵中每个元素${△}_{ij}^{(l)}$ 初始值为 0 , 会随着每个样本的学习而积累）

第L层（输出层）：${\delta }^{(L)}=a^{(L)}-y$

第L-1层：${\delta }^{(L-1)}={\left({\Theta }^{(L-1)}\right)}^T{\delta }^{(L)}\cdot \ast g^{\prime }\left(z^{(L-1)}\right)$

第L-2层：${\delta }^{(L-2)}={\left({\Theta }^{(L-2)}\right)}^T{\delta }^{(L-1)}\cdot \ast g^{\prime }\left(z^{(L-2)}\right)$

……

第1层（输入层）：不需要计算，因为不需要考虑输入数据的误差

权重值更新：${\Delta }_{ij}^{(l)}:={\Delta }_{ij}^{(l)}+a_j^{(l)}{\delta }_i^{(l+1)}$

3、计算D值：
$$D_{ij}^{(l)}:=\frac{1}{m}{\Delta }_{ij}^{(l)}+\lambda {\Theta }_{ij}^{(l)}$$
可以通过数学证明：（证明过程非常复杂，此处省略）
$$\frac{\partial }{\partial {\Theta }_{ij}^{(l)}}J(\Theta )=D_{ij}^{(l)}$$
也就是说，这里计算得到的 $D$ 值就是代价函数关于参数（权重值）的偏导数，接下来只需要使用梯度下降法去更新参数即可。

以上就是神经网络算法介绍，如果有疑问欢迎留言交流
最后，如果你对机器学习、数据挖掘、Python等内容感兴趣，欢迎关注我的博客