自动驾驶3D物体检测研究综述 3D Object Detection for Autonomous Driving: A Survey

本文介绍一篇最新的自动驾驶3D物体检测研究综述(2021年6月份发布),来源于中国人民大学,论文共26页,99篇参考文献。
论文链接为:https://arxiv.org/pdf/2106.10823.pdf
0. Abstract
自动驾驶被看作是避免人类遭受严重碰撞的最有希望的措施之一。其中,3D物体检测 是自动驾驶感知系统的核心基础,尤其是在路径规划、运动预测、碰撞避免等方面。
通常,在3D物体检测传感器标准布局中有立体/单目图像及相应的三维点云,其中点云能够提供准确的深度信息。但由于点云的稀疏性和不规则性,以及相机视角与激光雷达鸟瞰视角之间的错位导致的模态协同、远距离的遮挡和尺度变化等原因,点云3D物体检测仍处于起步阶段。
最近,有大量的文献正在研究这一视觉任务,3D物体检测已经取得了巨大进展。为此,本文全面回顾了这一领域的最新进展,包括传感器、基础知识和最新的检测方法及其优缺点。此外,本文还介绍了3D物体检测评价指标并对公开数据集做了定量比较。
1. Introduction
(引言里作者介绍了自动驾驶对社会的影响,什么是自动驾驶,什么是3D物体检测,我这里只摘取什么是3D物体检测。)
什么是3D物体检测:3D物体检测是从3D传感器数据中检测物理对象,估计3D边界框及物体类别。
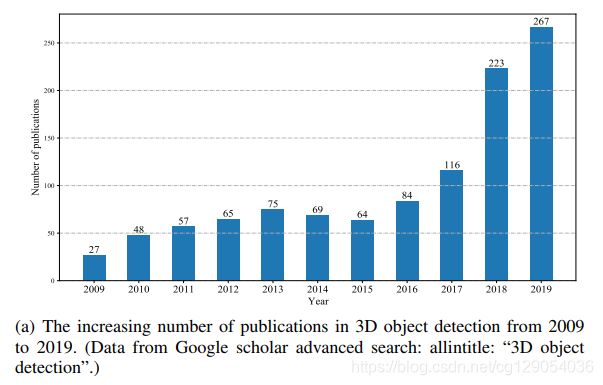
3D物体检测是3D场景感知和理解的核心。目前常见的3D表示有:point clouds、meshes、volumetric grids,其中点云在许多情况下是最好的表示。点云既不像由大量面组成的meshes消耗存储空间,也不像volumetric grids由于量化而丢失原始几何信息,而且点云与原始激光雷达数据很接近。
| Three types of commonly existing 3D representations | The number of publications in 3D object detection | The trend of heat change with time |
|---|---|---|
 |
 |
 |
2. Sensors
自动驾驶汽车常用的传感器可分为两类:被动传感器 (Passive Sensors)和主动传感器 (Active Sensors)。
-
被动传感器中
单目相机具有信息丰富的颜色和纹理属性、更好的路标文本视觉识别、高帧速率和可忽略不计的成本等优点,然而,它缺乏深度信息,这对于准确的位置估计至关重要。为了克服这一点,立体相机使用匹配算法来对齐左右图像中的对应关系以进行深度恢复。 -
主动传感器中
激光雷达是一种具有透镜、激光和探测器三个基本组件的点对点发射设备,发出的光脉冲将以三维点的形式从周围环境中反射回来,形成“点云“。高稀疏性和不规则性以及缺乏纹理属性是点云的主要特征,它与图像阵列有很好的区别,激光雷达的另一个问题是部署成本高。
下面的表格是单目相机、立体相机、激光雷达和固态激光雷达的优缺点比较。
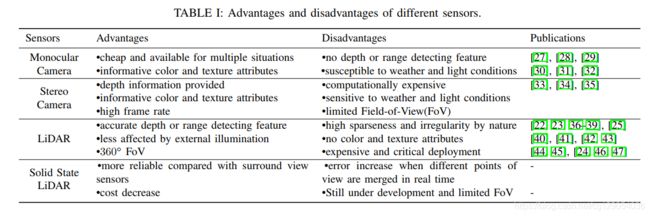
3. Fundamentals
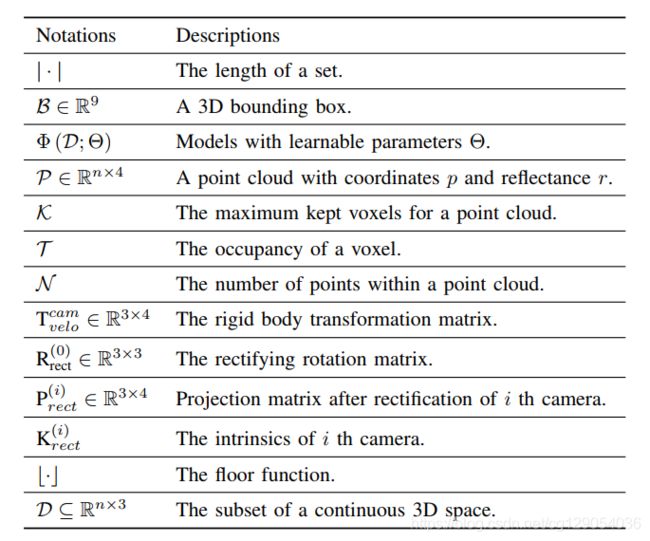
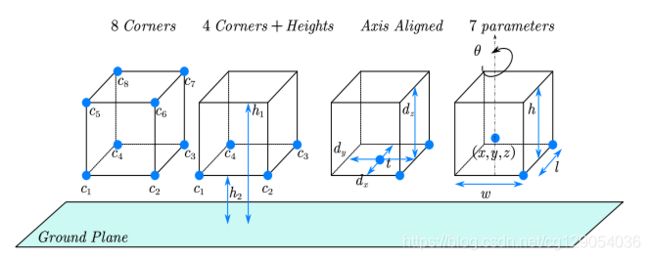
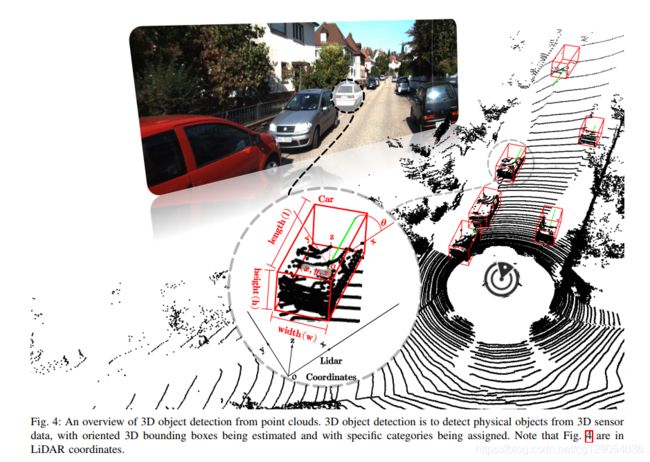
本文以KITTI自动驾驶数据集为例,下面是3D物体检测常用的符号规定、3D边界框的不同表达形式(常用的是7参数表达形式)、和3D物体检测的示意图(激光雷达坐标)。
| Commonly used notations | Comparison of the 3D bounding box parameterization | An overview of 3D object detection from point clouds |
|---|---|---|
 |
 |
 |
坐标转换:由于现有的研究算法大多是基于KITTI数据集,本文以KITTI数据集为例介绍如何进行坐标转换。KITTI数据集中激光雷达和相机坐标系定义为:
- 激光雷达坐标:x轴向前为正方向,y轴向左为正方向,z轴向上为正方向。
- 相机坐标:x轴向前为正方向,y轴向为下正方向,z轴向前为正方向。
激光雷达坐标中的一个3D点 p = ( x , y , z , 1 ) T p=(x,y,z,1)^{T} p=(x,y,z,1)T与对应的相机图像坐标 y = ( u , v , 1 ) T y=(u,v,1)^T y=(u,v,1)T之间的坐标转换关系为:
y = P rect ( i ) R rect ( 0 ) T velo cam p \mathrm{y}=\mathrm{P}_{\text {rect }}^{(i)} \mathrm{R}_{\text {rect }}^{(0)} \mathrm{T}_{\text {velo }}^{\text {cam }} \mathrm{p} y=Prect (i)Rrect (0)Tvelo cam p
其中,投影矩阵 P rect ( i ) \mathrm{P}_{\text {rect }}^{(i)} Prect (i)为:
P rect ( i ) = ( f u ( i ) 0 c u ( i ) − f u ( i ) b x ( i ) 0 f v ( i ) c v ( i ) 0 0 0 1 0 ) \mathrm{P}_{\text {rect }}^{(i)}=\left(\begin{array}{cccc}f_{u}^{(i)} & 0 & c_{u}^{(i)} & -f_{u}^{(i)} b_{x}^{(i)} \\ 0 & f_{v}^{(i)} & c_{v}^{(i)} & 0 \\ 0 & 0 & 1 & 0\end{array}\right) Prect (i)=⎝⎜⎛fu(i)000fv(i)0cu(i)cv(i)1−fu(i)bx(i)00⎠⎟⎞
则对应的相机内参 K rect ( i ) \mathrm{K}_{\text {rect }}^{(i)} Krect (i)为:
K rect ( i ) = ( f u ( i ) 0 c u ( i ) 0 f v ( i ) c v ( i ) 0 0 1 ) \mathrm{K}_{\text {rect }}^{(i)}=\left(\begin{array}{cccc}f_{u}^{(i)} & 0 & c_{u}^{(i)} \\ 0 & f_{v}^{(i)} & c_{v}^{(i)} \\ 0 & 0 & 1 \end{array}\right) Krect (i)=⎝⎜⎛fu(i)000fv(i)0cu(i)cv(i)1⎠⎟⎞
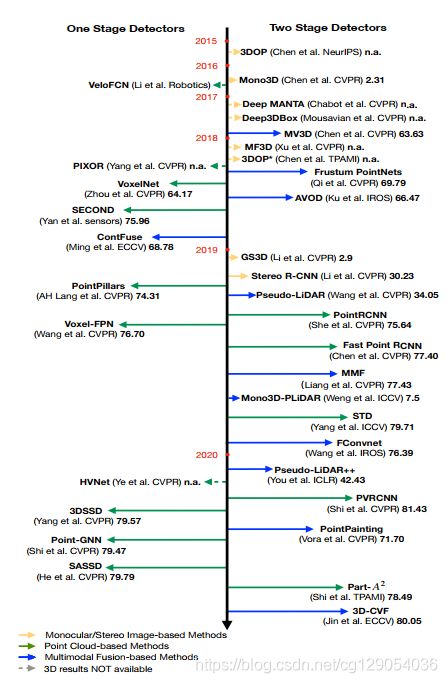
4. 3D Object Detection Methods
如下图所示,根据输入数据模态,3D物体检测方法可以分为基于单目/立体图像、基于点云和基于多模态融合·的方法,这里也将各种方法划分为一阶段和两阶段了。基于点云的检测方法还可以进一步细分为基于多视图、基于体素、基于点、基于点与体素四种方法。为了明确区分不同的基于多模态融合的方法,本文提出了两种新的融合策略:基于序列融合和基于并行融合的方法。
4.1 Monocular/Stereo Image-based Methods
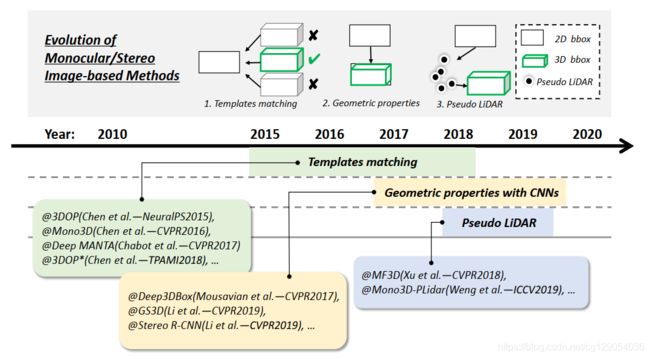
与二维物体检测方法十分相似,以单目/立体图像作为输入来预测三维实体。该方法通常可以分为三类(如下图所示):基于模板匹配和基于几何特性,以及基于图像的伪激光雷达方法。
4.2 Point Cloud-based Methods
卷积神经网络的本质是稀疏交互和权值共享,已被证明能够有效地利用规则域中的空间局部相关性,通过中心像素与其相邻像素的加权和。然而,由于点云是不规则和无序的,直接进行卷积操作,会遭受形状信息的缺失和点云序列方差。如下图所示,由于点云序列不同,其最终得到的特征往往也会不同。
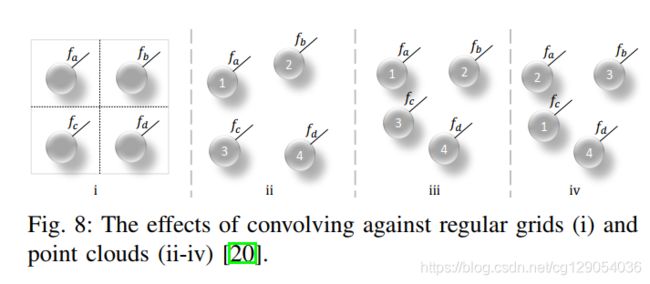
本文将基于点云的方法分为四类(如下图所示):基于多视图、基于体素、基于点云、基于点云体素的方法。
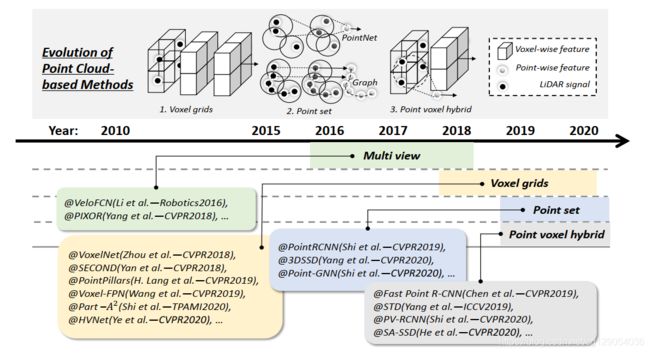
- Multi-view-based Methods:将点云转换为
前视图或鸟瞰图表示,然后使用CNNs和标准的2D物体检测算法处理。
| Visualization of point clouds from front view | Front View | Visualization of point clouds from bird’s eye of view | Bird’s Eye of View |
|---|---|---|---|
 |
 |
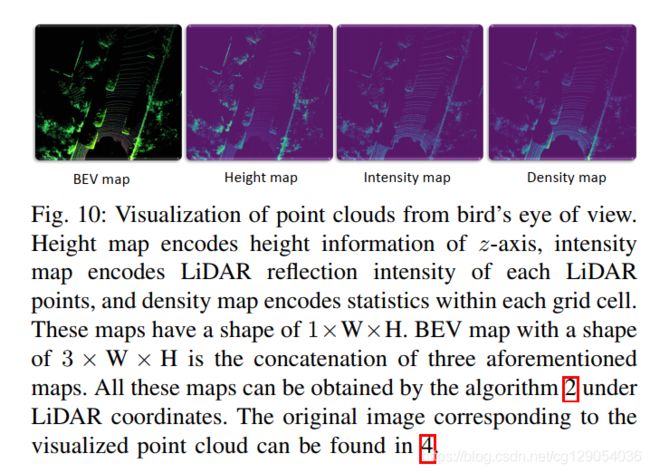 |
 |
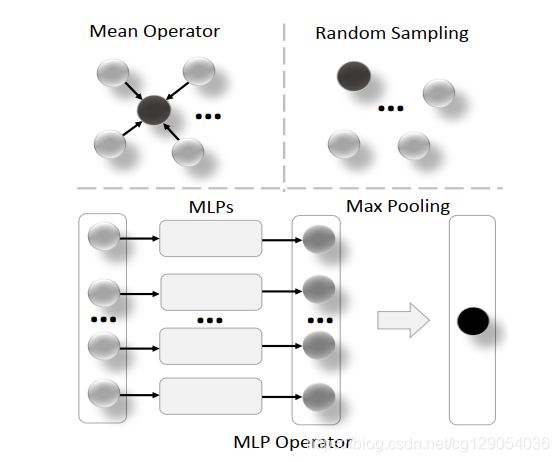
- Voxel-based Methods:将不规则点云转化为体素表示,通过 3D-CNNs 进行特征提取。基于体素的方法计算效率更高,但在离散化过程中不可避免导致信息丢失,导致定位精度下降。
下面是点云体素化的两种方式与三种聚合操作。
| Comparisons of hard voxelization and dynamic voxelization | Illustration of voxel-wise representations via three aggregation operators |
|---|---|
 |
 |
- Point-based Methods:使用原始点云数据,又两种类型方法:
PointNet(++)及其变体或图形神经网络(GNNs)。尽可能保留原始点云的几何图形。
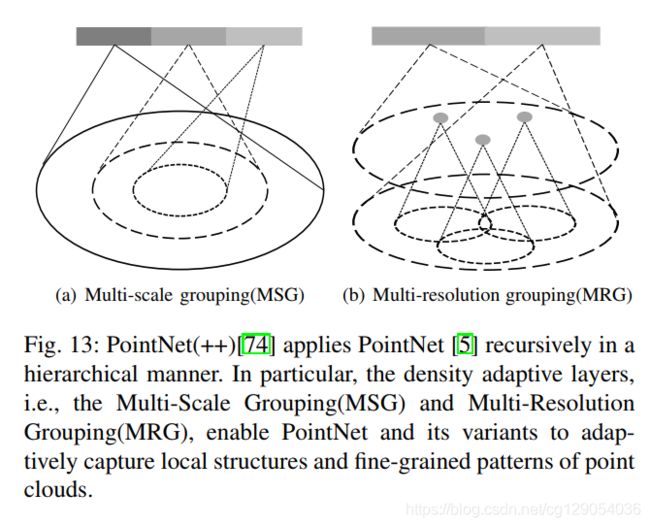
下面是PointNet++种提出的密度自适应层和最远点采样法。
| Farthest Points Sampling | |
|---|---|
 |
 |
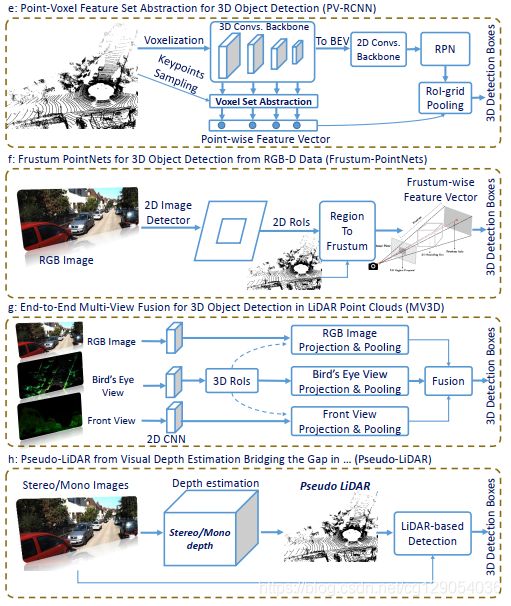
- Point-voxel-based Methods:点云特征学习的一个新的趋势,将体素特征与点的特征相结合。基于体素的特征表示方法会受到体素参数影响(低分辨率会导致粗粒度的定位精度,而高分辨率会增加计算量)。基于点的方法可以很容易地保留点云的不规则性和局部性,可以选择集合抽象,提供细粒度的邻域信息。
下面是几种有代表性的3D物体检测算法:
 |
 |
4.3 Multimodal Fusion-based Methods
现在,自动驾驶种的3D物体检测主要依赖激光雷达来提供周围环境信息。尽管激光雷达很精确,但是过度依赖单个传感器是不够明智的。此外,点云远距离分辨率低、纹理信息差也是一个很大的问题。所以自动驾驶中经常需要使用单目相机或双目相机进行多传感器融合,可以同时提供精细纹理和RGB属性。如下图所示,当涉及长距离时,在LiDAR中很难区分行人和路标。

下面是多模态融合的两种方式:前融合和后融合:
| General scheme for early fusion | General scheme for early fusion |
|---|---|
 |
 |
此外,本文还提出了两种新的融合方式:序列融合和并行融合。
- 基于序列融合:以顺序方式利用多阶段特征,其中当前特征提取依赖于前一阶段。
- 基于并行融合:在特征空间中进行融合,得到一个多模态的表示,然后输入到有监督的学习中去
5. Benchmark Evaluation
5.1 Metrics
这里以KITTI数据集为例,介绍了物体检测中的评价指标。这里有一个重要概念需要了解:IoU,如下图所示,表示了真值边界框与预测边界框的重合度,公式如下:
J ( B p , B g t ) = I o U 3 D = rotated 3 D area ( B p ∩ B g t ) rotated 3 D area ( B p ∪ B g t ) J\left(\mathcal{B}_{p}, \mathcal{B}_{g t}\right)=\mathrm{IoU}_{3 \mathrm{D}}=\frac{\text { rotated } 3 \mathrm{D} \operatorname{area}\left(\mathcal{B}_{p} \cap \mathcal{B}_{g t}\right)}{\text { rotated } 3 \mathrm{D} \operatorname{area}\left(\mathcal{B}_{p} \cup \mathcal{B}_{g t}\right)} J(Bp,Bgt)=IoU3D= rotated 3Darea(Bp∪Bgt) rotated 3Darea(Bp∩Bgt)

当IoU超过一个阈值时,就判定检测结果为真阳性(TP);反之为假阳性(FP),同时未检测到的真值边界框则为假阴性(FN)。精准率 P P P和召回率 R R R定义如下:
P = T P T P + F P = T P all det ections R = T P T P + F N = T P all ground truths P=\frac{T P}{T P+F P}=\frac{T P}{\text { all det ections }} \\ R=\frac{T P}{T P+F N}=\frac{T P}{\text { all ground truths }} P=TP+FPTP= all det ections TPR=TP+FNTP= all ground truths TP
在KITTI数据集中使用平均精准率(AP)来评价算法性能,计算公式如下:
A P = 1 N ∑ r ∈ S P interpolate ( r ) \mathrm{AP}=\frac{1}{N} \sum_{r \in S} P_{\text {interpolate }}(r) AP=N1r∈S∑Pinterpolate (r)
其中, P interpolate ( r ) = max r ~ : r ~ ≥ r P ( r ~ ) P_{\text {interpolate }}(r)=\max _{\tilde{r}: \tilde{r} \geq r} P(\tilde{r}) Pinterpolate (r)=maxr~:r~≥rP(r~),目前的KITTTI数据集使用的是40个召回率作为AP。
5.2 Comprehensive Comparsion of the State-of-the-arts
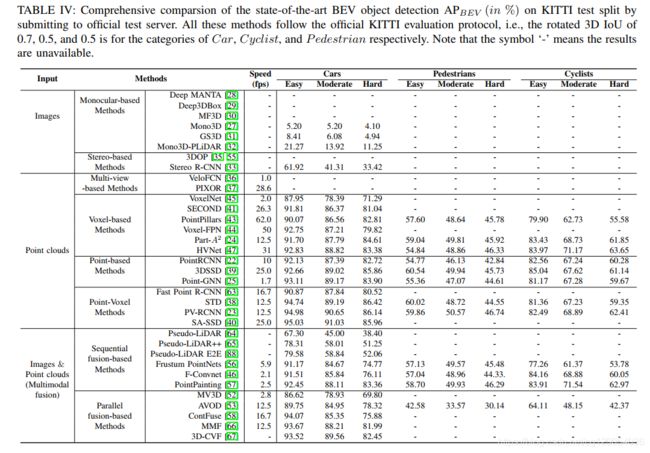
下面是各种3D检测算法在KITTI数据集上的3D检测性能和鸟瞰图检测性能比较。
| 3D object detection AP(%) | BEV object detection AP (%) |
|---|---|
 |
 |
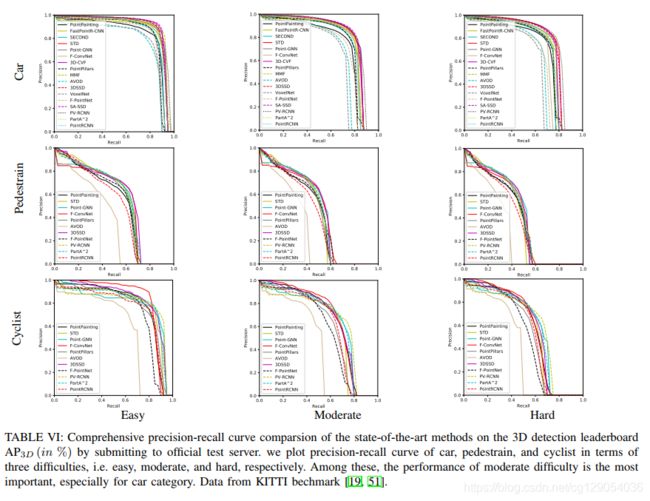
下面是各种3D检测算法在KITTI数据集上的3D检测和鸟瞰图检测的PRC曲线图。
| precision-recall curve on the 3D detection leaderboard | precision-recall curve on the BEV detection leaderboard |
|---|---|
 |
 |
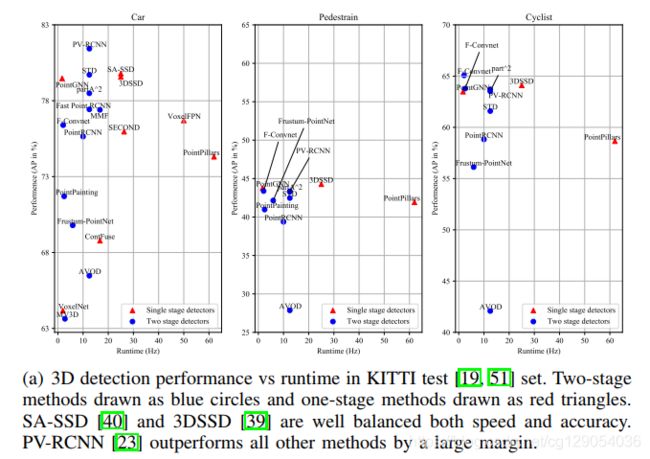
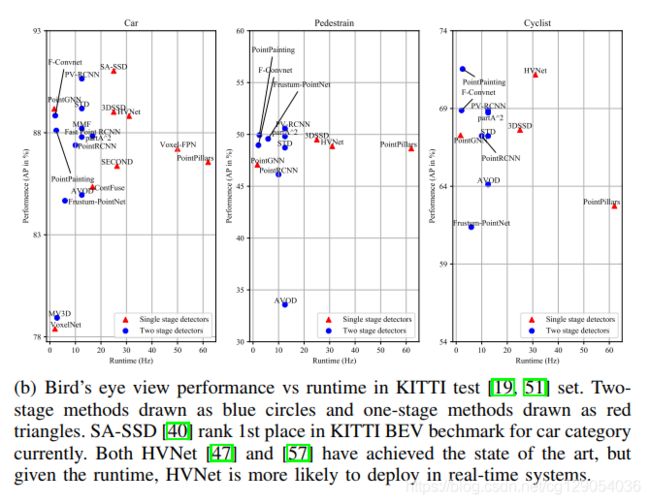
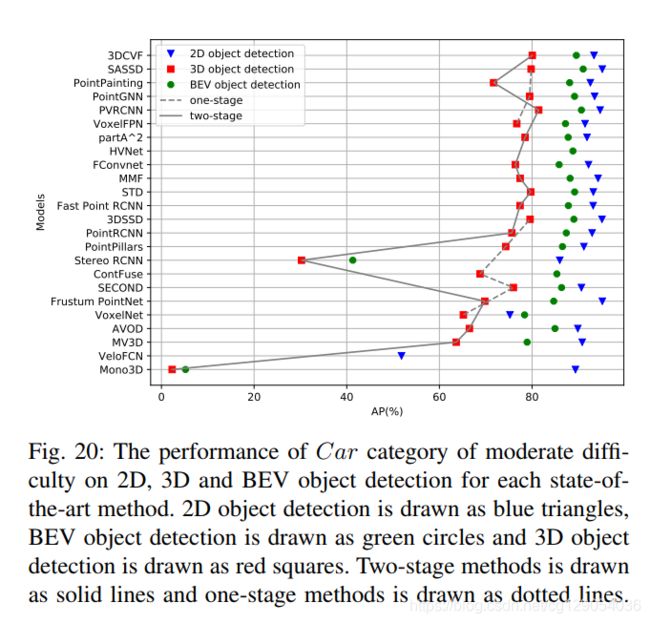
下面是各种3D检测算法在速度和准确率上的对比,以及3D、2D、鸟瞰图检测性能的比较。
| Performance vs Runtime(3D) | Performance vs Runtime(BEV) | 2D, 3D and BEV object detection |
|---|---|---|
 |
 |
 |
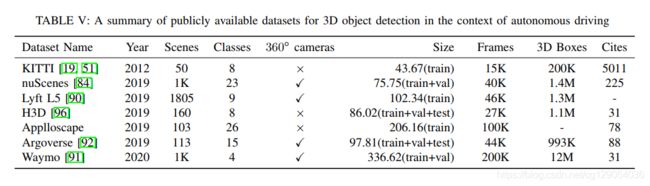
5.3 Emerging Datasets
5.4 Research Challenges and Opportunities
下面介绍了3D物体检测的未来研究方向:
- 由于缺少深度信息,基于图像的方法与现有的基于LiDAR的方法还存在很大的差距。立体相机或单目相机比激光雷达便宜几个数量级,可获得重要的纹理信息。此外,在发生故障的情况下,有一个备用传感器可以避免过度依赖单个传感器的安全风险。因此,
基于图像的方法仍然是一个很有前经的研究方向。 多模态融合理论上在获得更多信息时能产生更好的检测结果。然而,目前基于多模态融合的方法还远远落后于基于点云的方法。传感器同步和标定以避免随时间漂移对基于融合的方法也是一个巨大的挑战。如何将两者更好地结合在一起仍然是一个棘手的问题。- 使用
图神经网络进行3D物体检测的研究目前还很少。 基于点体素的方法(PV-RCNN,SA-SSD)是目前最有前景的研究方向之一,但仍有许多工作要做。伪激光雷达确实为处理图像数据提供了启示。另外,激光雷达与伪激光雷达融合也是一个值得努力的新方向。
6. Appendix
附录里作者额外介绍了3D物体检测中常用的4种损失函数:
- Basic loss :已知真值框为 ( x g t , y g t , z g t , w g t , l g t , h g t , θ g t ) \left(x^{g t}, y^{g t}, z^{g t}, w^{g t}, l^{g t}, h^{g t}, \theta^{g t}\right) (xgt,ygt,zgt,wgt,lgt,hgt,θgt),其anchor 框为 ( x a , y a , z a , w a , l a , h a , θ a ) \left(x^{a}, y^{a}, z^{a}, w^{a}, l^{a}, h^{a}, \theta^{a}\right) (xa,ya,za,wa,la,ha,θa),则两者定位回归残差为:
Δ x = x g t − x a d a , Δ y = y g t − y a d a , Δ z = z g t − z a h a , Δ w = log w g t w a , Δ l = log l g t l a , Δ h = log h g t h a Δ θ = sin ( θ g t − θ a ) , d a = ( w a ) 2 + ( l a ) 2 \Delta x=\frac{x^{g t}-x^{a}}{d^{a}} ,\Delta y=\frac{y^{g t}-y^{a}}{d^{a}}, \Delta z=\frac{z^{g t}-z^{a}}{h^{a}}, \Delta w=\log \frac{w^{g t}}{w^{a}}, \Delta l=\log \frac{l^{g t}}{l^{a}}, \Delta h=\log \frac{h^{g t}}{h^{a}} \\\Delta \theta=\sin \left(\theta^{g t}-\theta^{a}\right), d^{a}=\sqrt{\left(w^{a}\right)^{2}+\left(l^{a}\right)^{2}} Δx=daxgt−xa,Δy=daygt−ya,Δz=hazgt−za,Δw=logwawgt,Δl=loglalgt,Δh=loghahgtΔθ=sin(θgt−θa),da=(wa)2+(la)2
整个回归损失为:
L l o c = ∑ b ∈ ( x , y , z , w , l , h , θ ) SmoothL1 ( Δ b ) \mathcal{L}_{l o c}=\sum_{b \in(x, y, z, w, l, h, \theta)} \quad \text { SmoothL1 }(\Delta \mathrm{b}) Lloc=b∈(x,y,z,w,l,h,θ)∑ SmoothL1 (Δb)
分类损失为focal loss:
L focal ( p t ) = − α t ( 1 − p t ) γ log ( p t ) \mathcal{L}_{\text {focal }}\left(p_{t}\right)=-\alpha_{t}\left(1-p_{t}\right)^{\gamma} \log \left(p_{t}\right) Lfocal (pt)=−αt(1−pt)γlog(pt)
- IoU loss:这里提出了一个使用
IoU该作为置信度,公式为:
q = { 1 if iou > 0.75 0 if iou < 0.25 2 iou − 0.5 otherwise q=\left\{\begin{array}{ll} 1 & \text { if iou }>0.75 \\ 0 & \text { if } \text { iou }<0.25 \\ 2 \text { iou }-0.5 & \text { otherwise } \end{array}\right. q=⎩⎨⎧102 iou −0.5 if iou >0.75 if iou <0.25 otherwise
则损失函数为: L i o u = − [ q log ( p ) + ( 1 − q ) log ( 1 − p ) ] \mathcal{L}_{i o u}=-[q \log (p)+(1-q) \log (1-p)] Liou=−[qlog(p)+(1−q)log(1−p)]。
因此最终的损失函数为: L = 1 N pos ( β loc L loc + β iou L iou ) \mathcal{L}=\frac{1}{N_{\text {pos }}}\left(\beta_{\text {loc }} \mathcal{L}_{\text {loc }}+\beta_{\text {iou }} \mathcal{L}_{\text {iou }}\right) L=Npos 1(βloc Lloc +βiou Liou )。