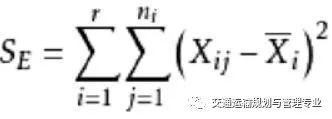kmeans设置中心_kmeans算法

k-means算法原理

K-means中心思想：事先确定常数K，常数K意味着最终的聚类类别数，首先随机选定初始点为质心，并通过计算每一个样本与质心之间的相似度(这里为欧式距离)，将样本点归到最相似的类中，接着，重新计算每个类的质心(即为类中心)，重复这样的过程，直到质心不再改变，最终就确定了每个样本所属的类别以及每个类的质心。由于每次都要计算所有的样本与每一个质心之间的相似度，故在大规模的数据集上，K-Means算法的收敛速度比较慢。

聚类算法：是一种典型的无监督学习算法，主要用于将相似的样本自动归到一个类别中。

聚类算法与分类算法最大的区别是：聚类算法是无监督的学习算法，而分类算法属于监督的学习算法，分类是知道结果的。

在聚类算法中根据样本之间的相似性，将样本划分到不同的类别中，对于不同的相似度计算方法，会得到不同的聚类结果，常用的相似度计算方法有欧式距离法。

k-means算法流程

1.选择聚类的个数k(kmeans算法传递超参数的时候，只需设置最大的K值)

2.任意产生k个聚类，然后确定聚类中心，或者直接生成k个中心。

3.对每个点确定其聚类中心点。

4.再计算其聚类新中心。

5.重复以上步骤直到满足收敛要求。(通常就是确定的中心点不再改变。)

k-means优点与缺点

优点：

1、原理简单(靠近中心点) ，实现容易

2、聚类效果中上(依赖K的选择)

3、空间复杂度o(N)时间复杂度o(IKN，N为样本点个数，K为中心点个数，I为迭代次数)

缺点：

1、对离群点， 噪声敏感 (中心点易偏移)

2、很难发现大小差别很大的簇及进行增量计算

3、结果不一定是全局最优，只能保证局部最优(与K的个数及初值选取有关)

k-means的经典案例与适用范围

1.文档分类器：根据标签、主题和文档内容将文档分为多个不同的类别。这是一个非常标准且经典的K-means算法分类问题。

2.物品传输优化：使用K-means算法的组合找到无人机最佳发射位置和遗传算法来解决旅行商的行车路线问题，优化无人机物品传输过程。

3.识别犯罪地点：使用城市中特定地区的相关犯罪数据，分析犯罪类别、犯罪地点以及两者之间的关联，可以对城市或区域中容易犯罪的地区做高质量的勘察。

4.客户分类聚类能过帮助营销人员改善他们的客户群(在其目标区域内工作)，并根据客户的购买历史、兴趣或活动监控来对客户类别做进一步细分。

5.球队状态分析：分析球员的状态一直都是体育界的一个关键要素。随着竞争越来愈激烈，机器学习在这个领域也扮演着至关重要的角色。如果你想创建一个优秀的队伍并且喜欢根据球员状态来识别类似的球员，那么K-means算法是一个很好的选择。

6.保险欺诈检测：利用以往欺诈性索赔的历史数据，根据它和欺诈性模式聚类的相似性来识别新的索赔。由于保险欺诈可能会对公司造成数百万美元的损失，因此欺诈检测对公司来说至关重要。

7.乘车数据分析：面向大众公开的Uber乘车信息的数据集，为我们提供了大量关于交通、运输时间、高峰乘车地点等有价值的数据集。分析这些数据不仅对Uber大有好处，而且有助于我们对城市的交通模式进行深入的了解，来帮助我们做城市未来规划。

8.网络分析犯罪分子：网络分析是从个人和团体中收集数据来识别二者之间的重要关系的过程。网络分析源自于犯罪档案，该档案提供了调查部门的信息，以对犯罪现场的罪犯进行分类。

9.呼叫记录详细分析：通话详细记录(CDR)是电信公司在对用户的通话、短信和网络活动信息的收集。将通话详细记录与客户个人资料结合在一起，这能够帮助电信公司对客户需求做更多的预测。

10.IT警报的自动化聚类：大型企业IT基础架构技术组件(如网络，存储或数据库)会生成大量的警报消息。由于警报消息可以指向具体的操作，因此必须对警报信息进行手动筛选，确保后续过程的优先级。对数据进行聚类可以对警报类别和平均修复时间做深入了解，有助于对未来故障进行预测。

sk-learns的参数详解与调优流程

不像监督学习的分类问题和回归问题，无监督聚类没有样本输出，也就没有比较直接的聚类评估方法。目前来讲有两种方法能够比较好的确定k的取值：

(1)惯性确定法，惯性只样本到其最近聚类中心的平方距离之和。基于欧几里得距离，K-Means算法需要优化的问题就是，使得簇内误差平方和(within-cluster sum of squared errors,SSE)最小，也叫簇惯性(cluster intertia)。随着分类数量的增多，SE的数值也会变得越来越小，但并不是分类数量越多越好，在选择时就需要选择‘拐点处的k值’后边有详细介绍。

SSE

(2)另一种方法是从簇内的稠密程度和簇间的离散程度来评估聚类的效果。常见的方法有轮廓系数Silhouette Coefficient和Calinski-Harabasz Index。个人比较喜欢Calinski-Harabasz Index，这个计算简单直接，得到的Calinski-Harabasz分数值s越大则聚类效果越好。Calinski-Harabasz分数值s的数学计算公式是：

Calinski-Harabasz

其中m为训练集样本数，k为类别数。Bk为类别之间的协方差矩阵，Wk为类别内部数据的协方差矩阵。tr为矩阵的迹。也就是说，类别内部数据的协方差越小越好，类别之间的协方差越大越好，这样的Calinski-Harabasz分数会高。在scikit-learn中， Calinski-Harabasz Index对应的方法是metrics.calinski_harabsaz_score.

实战案例-使用sk_learn里的KMeans模块进行演示：

import numpy as npimport matplotlib.pyplot as pltfrom sklearn.cluster import KMeansfrom sklearn.datasets import make_blobs ##为聚类产生数据集from sklearn import metrics#以下利用sklearn的make_blobs生成k-means测试数据n_samples=5000 #样本数量：5000random_state=10 #随机种子centers=5 #分类数x, y = make_blobs(centers=centers,n_samples=n_samples, random_state=random_state) #生成随机数plt.figure(figsize=(25, 25))plt.subplot(4,3,1)plt.scatter(x[:,0],x[:,1],c=y)plt.title('initial data')

生成的测试数据如下：

原始数据

对数据进行计算，n_clusters的取值范围在2~9，并记录每一个n_clustrs取值时的SSE与calinski_harabaz_score取值：

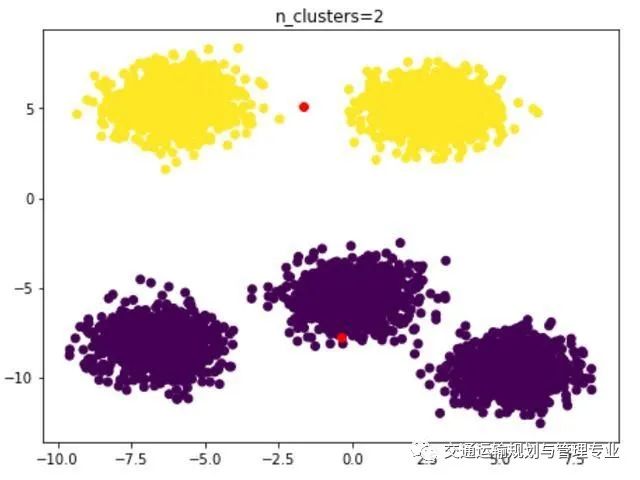
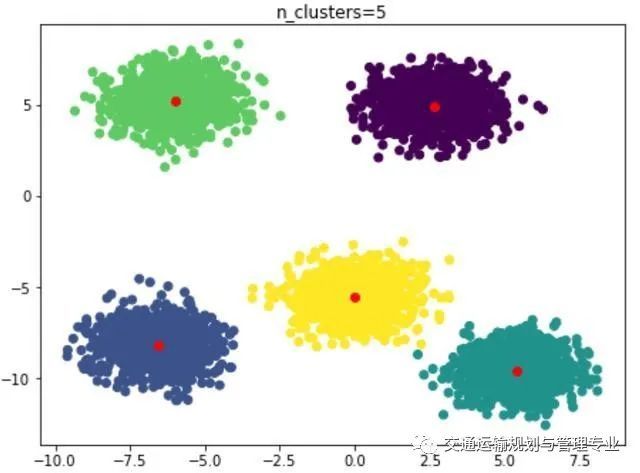
inertia=[]calinski_harabaz_score=[]a=2for i in range(2,10): km = KMeans(n_clusters=i,n_init=10,init='k-means++').fit(x) y_pred=km.predict(x) center_=km.cluster_centers_ inertia.append([i,km.inertia_]) z=metrics.calinski_harabaz_score(x, y_pred)  calinski_harabaz_score.append([i,z]) plt.subplot(4,3,a) a=a+1 plt.scatter(x[:,0],x[:,1],c=y_pred) plt.scatter(center_[:,0],center_[:,1],color='red') plt.title('n_clusters=%s'%i)inertia=np.array(inertia)plt.subplot(4,3,10)plt.plot(inertia[:, 0], inertia[:, 1])plt.title('SSE - n_clusters')plt.subplot(4,3,11)calinski_harabaz_score=np.array(calinski_harabaz_score)plt.plot(calinski_harabaz_score[:, 0], calinski_harabaz_score[:, 1])plt.title('calinski_harabaz_score - n_clusters')plt.show()

最终结果如下：n_clusters=2

n_clusters=2

n_clusters=5

n_clusters=5

n_clusters=9

n_clusters=9

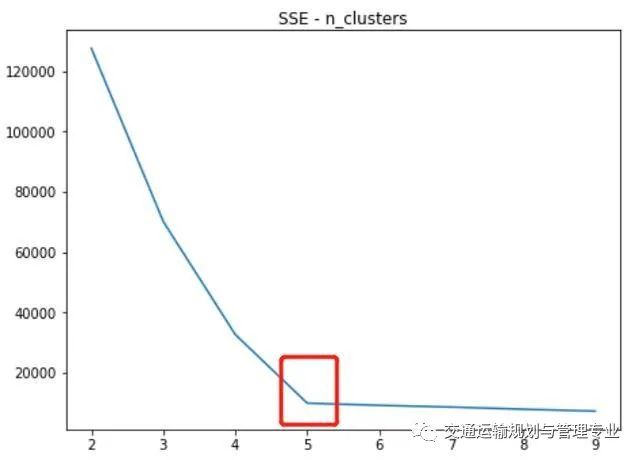
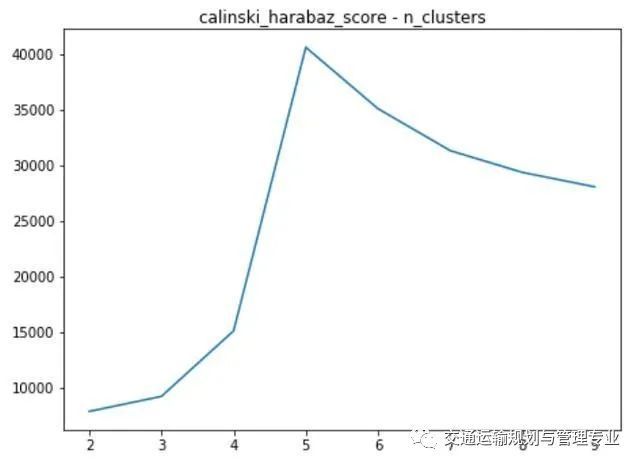
在不同的n_clusters取值情况下，SSE与calinski_harabaz_score的取值情况:

SSE随n_clusters变化

metrics.calinski_harabsaz_score随n_clusters的变化

通过SSE的定义可知，SSE随着n_clusters的增大是会变小的，一般会在SSE出现拐点的地方取值，同时还需要参考calinski_harabaz_score的取值。在此案例中能够看出，SSE在n_clusters=5的时候出现较大的拐点，calinski_harabaz_score在n_clusters=5的时候取得最大值。