代数多重网格AMG理论（C-AMG）的MATLAB代码学习心得

        最近在学习代数多重网格AMG理论，发现csdn上关于这方面内容比较少，于是自己看了一个很经典的matlab写的amg demo，分享一下关于Classic-AMG的学习新得，便于后人参考。我使用的demo可以从这个链接找到：AMG_matlab_demo

目录

什么是AMG？

程序层次结构

1 setup 准备阶段

2 Multigrid cycle 标准多重网格循环

程序流程简介

粗化算法

CAMG_GenerateCoarseGrid

CAMG_GetStrongDependencyMat

CAMG_InterpolateForPoint

多重网格迭代求解

总结

---

什么是AMG？

        代数多重网格（AMG）是利用几何多重网格（Geometric Multigrid, GMG）的一些重要原则和理念发展起来的不依赖于实际几何网格的多重网格方法。它继承了几何多重网格的主要优点，并且可以被用于更多类型的线性方程组。

        本文分享的是经典AMG理论，详情可以参考以下维基百科链接：C-AMG基本算法

程序层次结构

        我们知道，一个代数多重网格算法大致可以分为下述两个过程：

1 setup 准备阶段

        这部分构建代数多重网格的五个分量分别是各级网格信息，限制与插值算子，各级稀疏矩阵以及光顺方法，这部分是代数多重网格的重点过程，占了80%时间以上。

2 Multigrid cycle 标准多重网格循环

        这部分开始迭代求解，采用的算法与GMG几何多重网格方法完全一致，所以我们可以把重点放在第一的准备阶段上去。

        下面这几张图是程序的组成部分以及我自行制作的层次结构：

        

 

         其中test_Poisson2D&Generate2DMat_5P&Generate2DMat_9P这三个文件只是用来引入多重网格求解器，这里暂且忽略，FEM2D_data里有写好的A、b测试数据用来测试程序用。

程序流程简介

       首先我们打开Multigrid_Solver.m文件，看到程序给出的一些初始条件：

function [x, vcycle_cnt, rel_res] = Multigrid_Solver(A, b, smoother, pre_steps, pos_steps, rn_tol, max_vcycle)
% Multigrid solver for A * x = b using Classic AMG
% A          : [in]  The inital coefficient matrix
% b          : [in]  The right hand side
% smoother   : [in]  Function handle for a iterative method as a smoother
% pre_steps  : [in]  Number of iterations in the pre-smoothing
% pos_steps  : [in]  Number of iterations in the post-smoothing
% rn_tol     : [in]  The tolerance of the relative residual norm
% max_vcycle : [in]  Maximum number of V-clcyes to perform
% x          : [out] The solution after vcycle_cnt V-clcye
% vcycle_cnt : [out] Numbers of V-clcyes performed
% rel_res    : [out] Relative residual norm after each V-clcye

	if (nargin < 3) smoother   = @GS_Iter; end
	if (nargin < 4) pre_steps  = 1;	       end
	if (nargin < 5) pos_steps  = 1;	       end
	if (nargin < 6) rn_tol     = 1e-10;    end
	if (nargin < 7) max_vcycle = 100;      end
	
	n  = size(A, 1);
	x  = zeros(n, 1);
	rn = norm(b);
	vcycle_cnt = 0;
	rel_res(1) = rn;
	rn_stop    = rn * rn_tol;
	direct_n   = 16;
	PR_coef    = 1;
	
	% Generate coefficient matrices and interpolation operators of each level at once
	tic;
	[A_list, P_list, max_level] = CAMG_Vcycle_GenMat(A, direct_n);
	gm_t = toc;

       其中前后光滑次数最好都取1，direct_n为采用直接求解法时最小的矩阵规模，可以自行修改这个数值，PR_coef为P插值算子与R限制算子转换的系数，在我们得到插值算子P之后，通过求P的转置再乘以一个系数得到限制算子R（R=P'×PR_coef)，一般取1。

       之后通过CAMG_Vcycle_GenMat开始CAMG的准备阶段，我们打开CAMG_Vcycle_GenMat：

function [A_list, P_list, max_level] = CAMG_Vcycle_GenMat(A, direct_n)
% Generate the coefficient matrices for Classic AMG V-cycle
% A         : [in]  Original coefficient matrix
% direct_n  : [in]  Threshold for the smallest size of A in V-cycle
% A_list    : [out] The array of coefficient matrices on each level
% P_list    : [out] The array of interpolation (prolongation) operators on each level
% max_level : [out] Maximum level for V-cycle, initial is 1
	n = size(A, 1);
	A_list = {};
	P_list = {};
	level  = 1;
	A_list(level) = {A};
	
	while (n > direct_n)
		[CA, P] = CAMG_GenerateCoarseProblem(A);
		P_list(level) = {P};
		A_list(level + 1) = {CA};
		level = level + 1;
		A = CA;
		n = size(A, 1);
		
		nnz_ratio = nnz(A) / (size(A, 1) * size(A, 2));
		fprintf('Level %d, matrix size = %d,\t non-zero percentage = %2.4f \n', level, size(A, 1), nnz_ratio * 100.0);
	end
	max_level = level;
end

        可以看到定义几个细胞数组用来储存多级网格的系数矩阵以及网格间的插值算子，这里采用递推的方式来构建多级网格，先构建粗网格，然后把这一层粗网格当作下一次循环中的细网格。while循环内部判断当下网格系数矩阵维度数n大于直接求解判据direct_n时，继续构建更粗一级的网格，并且输出每级网格系数矩阵的非空值占比（一般情况下越粗的网格稀疏度就越低）。

       我们通过CAMG_GenerateCoarseProblem完成一层粗网格的生成，输入参数是本层网格系数矩阵，返回粗一级网格的系数矩阵CA，以及这两层网格间的传递算子P，具体实现方法我们来看下面AMG_GenerateCoarseProblem的具体代码：

function [CA, P] = CAMG_GenerateCoarseProblem(A)
% Using Classic AMG to generate the coarse grid matrix 
% and interlopation operator according to the input matrix
% A  : [in]  Fine grid problem matrix
% CA : [out] Coarse grid problem coefficient matrix
% P  : [out] Interpolation operator, CA = P^T * A * P
	
	is_cg_point = CAMG_GenerateCoarseGrid(A);
	cg_point_id = cumsum(is_cg_point);
	CA_n = sum(is_cg_point);
	A_n  = size(A, 1);
	sd_A = CAMG_GetStrongDependencyMat(A, 0.5);
	
	% Construct interpolation operator P
	P_rows = []; P_cols = []; P_vals = []; P_nnz = 0;
	n = size(A, 1);
	for curr_pid = 1 : n
		% P is CA_n cols, A_n rows, each row is a interplation relationship 
		% from coarse grid to fine grid
		[ip_id, ip_coef] = CAMG_InterpolateForPoint(curr_pid, A, sd_A, is_cg_point);
		for i = 1 : size(ip_id, 1)
			P_nnz = P_nnz + 1;
			P_rows(P_nnz) = curr_pid;
			P_cols(P_nnz) = cg_point_id(ip_id(i));
			P_vals(P_nnz) = ip_coef(i);
		end
	end
	P = sparse(P_rows, P_cols, P_vals, A_n, CA_n, P_nnz);
	
	% Construct coarse grid matrix
	CA = P' * A * P;
end

       要生成粗网格第一步首先应在细网格上根据某种规则找到粗网格点，一般采用RS粗化准则的较多，但本程序使用的是如下粗化算法：

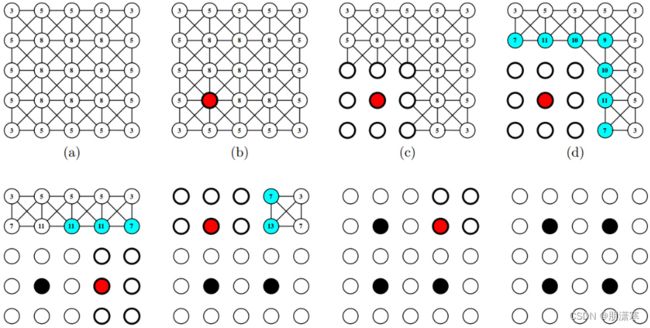
粗化算法

     首先将系数矩阵包含的网格信息转化为一副无向邻接图

1. 为图上每一个点赋权重，权重值等于其邻接的点的个数；
2. 选取当前图上未被分类的点中权重最大的点，将其加入粗网格格点集，将其所有邻居加入细网格格点集；
3. 对于所有新加入细网格格点集的点，将它们的邻居的权重 +1；
4. 重复 2-3，直至所有点都被分配完毕。

       具体实现过程我们来看CAMG_GenerateCoarseGrid函数：

---

CAMG_GenerateCoarseGrid

        由于代码过长这里不放全部代码，有需要的可以从开头链接处自行下载获得完整代码。

    n = size(A, 1);
	edge_list = (A ~= 0);
	edge_list = edge_list - diag(diag(edge_list));  % Remove the diagonal 
	x_degree  = edge_list * ones(n, 1);
	cg_point  = -ones(n, 1);
	
	unvisited_points = sum(cg_point == -1);

       这里A~=0获得了系数矩阵的非零项，我们知道系数矩阵暗含网格关系，非零项也就表示用系数矩阵的行列值表示的这两个点之间有连接关系，我们暂且忽略实际网格中这两个点的信息，只要这两个点相邻，就把保存着网格点间邻接关系信息的逻辑值存入edge_list，去对角项是因为系数矩阵的对角项没有保存不同点间的信息。 

       x_degree为上述粗化算法第一步中每个点的权重值，先初始化一个负单位列向量为所有网格点，未访问点个数就是cg_point中为负一元素的个数，之后我们通过粗化算法去遍历访问每一个网格点 ：

while unvisited_points > 0
		% Find next coarse grid point
		[~, new_cg_point] = max(x_degree); 
		cg_point(new_cg_point) = 1;
		x_degree(new_cg_point) = 0; 
		
		% Find new fine grid point neighbors
		neighbors = find(edge_list(new_cg_point, :) == 1);
		new_neighbors = [];
		for i = 1 : size(neighbors, 2)
			if (cg_point(neighbors(i)) == -1)
				new_neighbors = [new_neighbors neighbors(i)];
				% Mark new neighbors
				cg_point(neighbors(i)) = 0;  
				x_degree(neighbors(i)) = 0; 
			end
		end

上述代码段对应的图

       上面这段代码是寻找并标记粗网格点以及他的相邻点，我们先找到一个权重最大的点将其加入粗网格点集(令此位置点的cg_point=1)，之后通过find函数找到刚才这个点的所有相邻点，之后标记这些相邻点加入细网格点集（令此位置点的cg_point=0)，在new_neighbors中储存每个邻居点在edge_list的位置信息。

        % Mark new neighbors and add their unvisited neighbors' weight
		for i = 1 : size(new_neighbors, 2)
			curr_neighbor = new_neighbors(i);
			
			nn = find(edge_list(curr_neighbor, :) == 1);
			nn2 = [];
			for i = 1 : size(nn, 2)
				if (cg_point(nn(i)) == -1)      % Only update those unvisited neighbors
					nn2 = [nn2 nn(i)];
				end
			end
			
			for i = 1 : size(nn2, 2)
				x_degree(nn2(i)) = x_degree(nn2(i)) + 1;
			end
		end
		
		unvisited_points = sum(cg_point == -1);
	end

上述代码段对应的图

         

       上面这段代码对应粗化算法的第三步，nn = find(edge_list(curr_neighbor, :) == 1);这一句我们找到与刚才找到的一个粗网格点的邻居点相邻的点，之后通过nn2 = [nn2 nn(i)]把它们的位置信息储存在nn2里，通过x_degree(nn2(i)) = x_degree(nn2(i)) + 1，令每个刚才加入细网格点集的点的邻居点权重加一，这里要注意一定是还未访问过的点才可这样操作（对应if (cg_point(nn(i)) == -1)这句），最后统计所有未访问的点数量，如果所有点都已访问过，循环结束返回粗网格点信息。

---

CAMG_GetStrongDependencyMat

       在C-AMG 中插值和限制投影算子的定义依赖于边权大小，首先需获知不同点间的强弱连接关系，看下述代码：

function sd_mat = CAMG_GetStrongDependencyMat(A, theta)
% Mark all strong dependency in the graph that 
% $-a_{ij} >= theta * max_{k != i} {-a_{ik}}$
% A      : [in]  Edge list of a weighted directed graph 
% theta  : [in]  Strong dependency threshold
% sd_mat : [out] Edge list, marked strong connections: 1 for true, -1 for false
	n = size(A, 1);
	sd_mat = sparse(n, n);
	for row = 1 : n
		threshold  = theta * max(-A(row, :));
		if (threshold == 0)
			continue;
		end
		nnz_in_row = find( A(row, :) ~= 0);         
		nnz_in_row = setdiff(nnz_in_row, [row]);    % Ignore diagonal element
		sd_in_row  = find(-A(row, :) >= threshold);
		wd_in_row  = setdiff(nnz_in_row, sd_in_row);
		sd_mat(row, sd_in_row) =  1;
		sd_mat(row, wd_in_row) = -1;
	end
end

       根据强连接点的定义：给定阈值 0<θ≤1, 我们称变量ui 强依赖于uj , 如果满足以下关系： 

       这段代码相对好理解一些，threshold即是不等式右侧的表达式值，只需要找到每个点的所有邻居点（nnz_in_row = find( A(row, :) ~= 0)）然后判断其对应的系数矩阵值与threshold大小关系，即可得到不同点间的强弱连接关系。

---

CAMG_InterpolateForPoint

       得到强弱连接关系后我们就可以开始构建插值算子，详情参考：C_AMG基本算法

插值算子构建算法

       对于function [ip_id, ip_coef] = CAMG_InterpolateForPoint(curr_pid, A, sd_A, is_cg)每次传入一个网格点id、系数矩阵、网格点间的连接关系，以及粗网格点信息，返回这个点的所有邻接粗网格点ip_id以及周围粗网格点对此位置插值的贡献值。

if (is_cg(curr_pid) == 1)
		ip_id   = curr_pid;
		ip_coef = 1;
		return;
	end

       首先判断传入的点是否是粗网格点，如果是，则不需要进行插值。

    % Find all coarse grid points for interpolation
	neighbors = find(A(curr_pid, :) ~= 0);
	neighbors = setdiff(neighbors, curr_pid); %删对角线
	neighbors_cnt = size(neighbors, 2);
	ip_cnt  = 0;
	ip_id   = zeros(neighbors_cnt, 1);
	ip_coef = zeros(neighbors_cnt, 1);
	for i = 1 : neighbors_cnt
		curr_neighbor = neighbors(i);
		if (is_cg(curr_neighbor) == 1)
			ip_cnt = ip_cnt + 1;
			ip_id(ip_cnt)   = curr_neighbor;
			ip_coef(ip_cnt) = A(curr_pid, curr_neighbor);
		end
	end
	ip_id = ip_id(1 : ip_cnt);      %0项删除掉
	ip_coef = ip_coef(1 : ip_cnt);

       上面这段代码是在寻找插值点附近的所有粗网格点，先找到插值点附近所有的邻居点存在neighbors里，之后通过if (is_cg(curr_neighbor) == 1)找到这些邻居点中属于粗网格点的部分，直接用粗网格点对应的系数矩阵值来更新插值算子系数。

    % Redistribute the edge weight of all fine grid points with weak dependency
	a_ii_new = A(curr_pid, curr_pid);
	for i = 1 : neighbors_cnt
		curr_neighbor = neighbors(i);
		if ((is_cg(curr_neighbor) == 0) && (sd_A(curr_pid, curr_neighbor) == -1))
			a_ii_new = a_ii_new + A(curr_pid, curr_neighbor);
		end
	end

       上面这段代码对应插值算法构建的第一步，重分配弱连接点的边权给插值点。if ((is_cg(curr_neighbor) == 0) && (sd_A(curr_pid, curr_neighbor) == -1))这一句是在寻找细网格弱连接点。

    % Redistribute the edge weight of all fine grid points with strong dependency
	for i = 1 : neighbors_cnt
		curr_neighbor = neighbors(i);
		if ((is_cg(curr_neighbor) == 0) && (sd_A(curr_pid, curr_neighbor) == 1))
			cg_neighbor_list = [];
			cg_neighbor_weight_sum = 0;
			
			% Find all coarse grid points connected to curr_neighbor
			% and sum the edge weight of these connections
			for j = 1 : neighbors_cnt
				curr_check_neighbor = neighbors(j);
				if ((is_cg(curr_check_neighbor) == 1) && (A(curr_neighbor, curr_check_neighbor) ~= 0))
					cg_neighbor_weight_sum = cg_neighbor_weight_sum + A(curr_neighbor, curr_check_neighbor);
					cg_neighbor_list = [cg_neighbor_list j];
				end
			end
			
			% Redistribute the edge weight A(curr_pid, curr_neighbor) to each 
			% neighboring coarse grid point
			for k = 1 : size(cg_neighbor_list, 2)
				j = cg_neighbor_list(k);
				curr_check_neighbor = neighbors(j);
				contrib = A(curr_neighbor, curr_check_neighbor) / cg_neighbor_weight_sum * A(curr_pid, curr_neighbor);
				
				ip_id_pos = find(ip_id == curr_check_neighbor);
				ip_coef(ip_id_pos) = ip_coef(ip_id_pos) + contrib;
			end
		end
	end
	
	% Normalize the coefficients
	ip_coef = ip_coef ./ -a_ii_new;
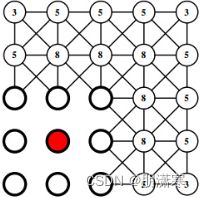
end

       这段代码则重分配强连接点的边权给自身与插值点都相邻的粗网格点。为了形象地描述这个过程，引入链接中的这个例子：图中中心点为 ui,待插值。N, W, S, E 四个点是粗网格点，NE, NW 是 ui 强连接的细网格点，SE, SW 是 uiui 弱连接的细网格点，边上各数值为边权。

         if ((is_cg(curr_neighbor) == 0) && (sd_A(curr_pid, curr_neighbor) == 1))就是找到NW与NE中的一个点，位置信息储存在curr_neighbor里。以j为参数的for循环里新增参数curr_check_neighbor，语句if ((is_cg(curr_check_neighbor) == 1) && (A(curr_neighbor, curr_check_neighbor) ~= 0))找到与NW或NE中某一个点有相邻关系的粗网格点，统计NW或NE中某一个点对他们的贡献和，并统计这些粗网格点的位置信息（cg_neighbor_list = [cg_neighbor_list j];），通过上述第三步的公式将NW与NE的边权重分配给W、N、E粗网格这三个点（ip_coef(ip_id_pos) = ip_coef(ip_id_pos) + contrib;），其中的contrib即是NW、NE对W、N、E重分配边权的贡献值。

        最终，套用公式令ip_coef = ip_coef ./ -a_ii_new;得到本插值点的插值算子系数，上述这个过程一共要进行当前网格的网格点数量次数。

---

       回到CAMG_GenerateCoarseProblem，通过P_rows、 P_cols、 P_vals三个向量即可构建插值算子的系数矩阵P，限制算子R=P'，自然得到粗网格稀疏矩阵CA = P' * A * P。

---

       回到CAMG_Vcycle_GenMat，不断重复上述CAMG_GenerateCoarseProblem过程直到最粗一级网格维数小于直接求解判据为止。至此代数多重网格的准备阶段（setup）完成。

---

多重网格迭代求解

       本程序采用了标准多重网格的Vcycle迭代方式与标准的高斯赛德光滑方法，网上已有很多资料介绍因此不做过多说明，值得注意的是这里新增了R与P间转换的一个系数PR_coef，令R = P' * PR_coef;这个系数的引入对于整个迭代求解的收敛速度有了新的影响，但具体如何取值我并没有进行实验。

总结

         本文是我学习了Classic_AMG_Demo-master后的一些心得，对程序进行了简单说明，由于时间匆忙以及参考资料缺少，不能保证100%的正确性，欢迎大家随时对我文中出现的问题提出质疑，共同交流共同进步！