基于隐式神经网络表达的数据压缩

数据压缩是一种在日常生活中广泛应用的技术，从算法角度来讲，压缩的过程是通过改变数据的表征范式以达到保留信息、去除冗余的过程。近来，深度学习在数据压缩领域的应用不仅表现出极好的性能，还为数据表征提出了具有启发性的新范式。

基于隐式神经网络表达（Implicit Neural Representation）的数据压缩模型以函数表征数据、其函数拟合数据的过程就是压缩过程，近期的工作表示[1][2][3]，基于INR的数据压缩模型网络结构简单，拟合迅速，并在语音、图片、甚至气象数据的压缩上超越传统算法。

学习基于INR的数据压缩算法可以拆解为对两个问题的探索，首先是INR模型如何表征数据，其次是如何训练INR模型。

问题一 INR如何表征数据？

根据通用近似定理[4]可知，给定合适的权重，神经网络可以非常简单的网络架构来逼近非常复杂函数，也就是说，以多层感知机构成的神经网络可以拟合一段语音的信号分布、一个图片的像素值分布、甚至是一个三维场景的体密度分布。

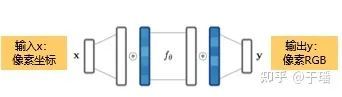
举例来讲，以图片的压缩为例，已知神经网络f1已经拟合并表征图片d1，那么在给定像素坐标x时，可以求得x处像素值为y = f1(x)，而在输入所有像素坐标后，可以求得整张图片的像素值，从而得到由函数f1表征的图片d1（见图1）。

同样的原理，神经网络f2可以表征图片d2，以此类推，神经网络就成为了数据的“函数式”表征（见图2）。

那么INR模型f1与f2之间有什么关联呢？在基于INR表征数据的算法中，表征同类数据（如图片、三维场景等）的INR模型拥有同样的结构、不同的权重。基于[2][3]可以得知，INR模型可以被分为基模型与调制模型，其中基模型对应权重为预训练得出，调制模型对应权重为基于不同数据样本进行增量训练得出，也就是说，f1与f2只有调制权重不同，而调制权重在整个模型权重中稀疏性极高。

基于上述的描述，我们可以得知，n张图片可以被一个基模型和n组调制权重表征，每组调制权重就是对应图片的压缩后的数据表征形式。

问题二 如何训练INR模型？

在了解INR模型拥有表征数据的能力后，第二个问题就是如何训练INR模型来迅速的拟合数据呢？数据压缩技术的应用场景繁多，其中无线通信的信号压缩等场景对实时性要求极高，所以INR模型的高性能训练与高效的拟合优化策略也至关重要。

在问题一的探讨中提到，INR模型可以分为基模型和调制模型，其中基模型的训练是离线进行，调制模型的训练是基于压缩的目标数据进行的权重微调过程，是在线进行。为了提升压缩效率，调制模型训练的实时性至关重要，考虑到以上诉求，COIN++ [2]中将元学习方法MAML[5]引入，以提升INR模型的训练效率。

MAML是一种模型优化方法，其目的在于针对一个模型学习最佳的初始化权重，从而使得该模型面向不同的任务进行训练时可以通过极少次权重更新收敛；其过程有两步，inner loop计算在给定初始化权重的情况下少次权重更新后的损失，outer loop则根据该损失优化初始化权重。

在INR模型训练的语境下，MAML可以被这样理解：其目的在于针对INR模型学习最佳的基模型权重，从而INR模型在面对不同数据时可以通过极少次的调制权重更新达到拟合的目的；其过程中inner loop只更新调制权重来计算压缩损失，outer loop则根据损失优化基模型权重。通过运用元学习方法，基于INR的数据压缩算法在压缩效率大大提升。

在COIN++的基础上，Functa [3]进一步提升了基于INR的数据压缩效率，直接运用生成类网络对调制权重进行预测，而其中生成类网络的训练数据集则是由元学习训练出的调制权重组成。

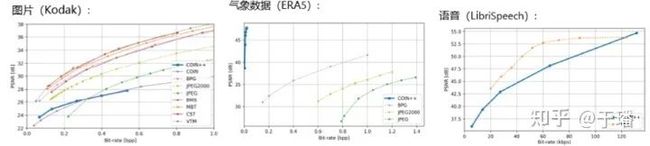
以上是基于INR的数据压缩技术概览，那么该计算在数据压缩场景中的效果如何呢？根据COIN++中实验结果可以看出，在压缩气象数据时表现出远远超越了传统方法的效果，而在压缩图片、语音数据时则只在有限的压缩比例下超越传统方法（见图3）。

综上所述，基于INR的数据压缩技术是一个非常有前景的研究方向，针对不同模态数据适用的INR模型结构、调制权重的稀疏性、以及拟合优化策略都值得进一步探索，同时， “通过模型拟合数据”的思想在实际场景中的应用也有很大的价值。

首先，INR模型的大小、结构、训练难度是与信息复杂度成正比，而非原数据的分辨率，这使得时空相关性强的数据能够得到卓越的压缩效果，达到极致的去除冗余信息的效果，其次， INR模型在被解压时，输入采样点可控制解压后数据的分辨率，用户可以自由的进行数据的部分解压、低分辨率解压、甚至是超分辨率解压。

[1] Emilien Dupont et al. “Coin: Compression with implicit neural representations”. In: arXiv preprint

arXiv:2103.03123 (2021).

[2] Emilien Dupont et al. “Coin++: Data agnostic neural compression”. In: arXiv preprint arXiv:2201.12904(2022).

[3] Emilien Dupont et al. “From data to functa: Your data point is a function and you should treat it like one”.In: arXiv preprint arXiv:2201.12204 (2022).

[4] Hornik, Kurt; Stinchcombe, Maxwell; White, Halbert (1989). Multilayer Feedforward Networks are Universal Approximators (PDF). Neural Networks. Vol. 2. Pergamon Press. pp. 359–366.

[5] Chelsea Finn, Pieter Abbeel, and Sergey Levine. Model-agnostic meta-learning for fast adaptation

of deep networks. In International Conference on Machine Learning, 2017.