神经辐射场的几何编辑CVPR2022
目录
- 摘要
- 1.引言
- 2.相关工作
-
- 2.1.新视图合成
- 2.2.3D编辑方法
- 3.方法
-
- 3.1.神经辐射场
- 3.2.显式曲面网格表示的编辑
- 3.3.变形转换到离散体积(Discrete Volume)
- 3.4.光线弯曲
- 4.实验
-
- 4.1.数据集和metrics
- 4.2.实验结果
摘要
隐式神经渲染,特别是神经辐射场(NeRF),在场景的新视图合成中显示出巨大潜力。然而,当前基于NeRF的方法无法使用户在场景中执行用户控制的形状变形(user-controlled shape deformation)。虽然现有的工作已经提出了一些根据用户的约束(user’s constraints)修改辐射场的方法,但修改仅限于颜色编辑或对象的平移和旋转。在本文中,我们提出了一种方法,允许用户对场景的隐式表示执行可控的形状变形,并合成编辑后场景的新视图图像,并且无需重新训练Nerf。具体而言,我们建立了目标场景的显式mesh表示(网格表示)和隐式neural表示之间的对应关系。用户可以首先利用完善的基于mesh的变形方法来变形场景的mesh表示。然后,我们的方法利用用户对mesh表示的编辑,通过引入四面体网格(tetrahedra mesh)作为代理来弯曲相机光线,从而获得编辑场景的渲染结果。大量的实验表明,我们的框架不仅可以在合成数据上实现理想的编辑效果,而且也可以在用户捕获的真实场景上实现良好编辑效果。
1.引言
新视角的视图合成在计算机视觉和计算机图形学中得到了广泛的研究。特别是最近提出的神经辐射场(NeRF)激发了大量后续工作,Nerf的相关工作旨在实现更好的视觉效果,更快的渲染速度,不同场景的泛化,应用于动态场景,减少输入视图。然而,作为一种隐式建模方法,神经辐射场很难让用户编辑或修改场景对象,而显式表示相对容易。网格表示(mesh representation)作为一种显式表示(explicit representation),通常用于形状建模和渲染(shape modeling and rendering)。有许多关于网格变形或编辑的研究工作。然而,一般很难获得真实场景的精确显式表示。从稀疏图像集,可以使用一些多视图立体(MVS,Multi-View Stereo)方法来重建场景的点云或网格表示,但质量通常较差。因此,基于隐式表示(如NeRFs)的新视图合成能力,进一步研究如何编辑隐式表示已成为一个新的探索方向。
一些工作已经研究了如何编辑NeRF。例如,EditingNeRF是第一个提出对隐式辐射场进行编辑的。他们在同一类别的一组合成3D模型上进行训练,如ShapeNet中的椅子和桌子,并引入形状编码和颜色编码分别表示不同模型的几何和外观。用户选择所需的颜色并在指定视图的图像上绘制一些粗略的涂鸦,以指示应更改的内容。然后,通过基于原始图像和编辑图像之间的loss更新网络,将局部编辑传播到3D区域。该工作仅限于颜色修改或形状的某些部分的移除,并且不可能对形状进行实质性修改,例如形状变形。最近的一项工作,ObjectNeRF,提出学习分解神经辐射场,将物体和背景分开。因此,它可以复制、移动或旋转对象以进行可编辑的场景渲染。然而,它也不支持形状变形。同时,一些工作考虑使用NeRF对动态场景建模,并使用多层感知器(MLP)预测场景变化。然而,它们要么限制对人体的编辑,要么只能从录制的视频中学习运动信息,不能执行主动编辑。
在本文中,我们提出了一种编辑神经辐射场的方法,该方法结合了显式表示中便于局部编辑的优点和隐式表示中真实渲染效果的优点。与之前的工作(EditingNeRF和ObjectNeRF)不同,我们专注于场景的几何内容,如图1所示,支持用户编辑场景几何,并可以在新视图中执行真实感渲染。这是第一个在一般场景的NeRF上执行用户控制形状变形的工作。为此,我们首先从训练好的NeRF中提取显式三角网格表示(triangular mesh representation)。用户对显式网格表示进行直观地变形。接下来,从三角形网格表示上构建四面体网格,四面体网格将三角形网格包围。我们使用三角形网格的变形来驱动四面体网格的变形,从而将场景几何曲面的变形传播到空间离散变形场。最后,我们使用四面体顶点插值来完成从离散变形场到连续变形场的传播。穿过四面体网格的光线将在连续变形场之后做相应弯曲,以便最终渲染结果符合用户的编辑。我们的方法是通用的,不限于人体等特定形状,适用于动物和一般物体等任意形状。
- 图1:我们提出了一种编辑静态神经辐射场(NeRF)的方法。用户只需要捕获多视图图像来构建NeRF表示,然后他们就可以显式直观地编辑场景的隐式表示。我们的方法可以对包含多个对象的场景几何体执行用户控制的形状变形。
2.相关工作
我们的NeRF编辑框架为编辑神经隐式场景表示的新视图合成提供了新的范例。这里,我们总结了新视图合成和3D变形(或3D编辑)方法的相关工作。
2.1.新视图合成
为了从给定的输入图像推断逼真的新视图合成结果,先前的工作依赖于真实世界场景的显式或隐式几何表示。最近,神经渲染取得了巨大的进展。它采用深度神经网络合成图像,可用于多种表示,如体素、点云、网格、多平面图像(MPIs,multi-plane images)和隐式场(implicit fields)。作为代表性作品之一,神经辐射场(NeRF)吸引了大量关注,它使用多层感知器(MLP)对场景的几何结构和外观进行建模。NeRF可以实现具有输入视图相关效果的新视图图像的逼真合成。然而,NeRF仍有缺点,大量工作扩展了原始NeRF,包括更好的合成效果,适用于动态场景,更快的渲染速度,对不同场景的泛化等等。在这项工作中,我们专注于 NeRF 的几何编辑(变形)。 如前所述,EditingNeRF提出在渲染图像上进行编辑,并使用网络优化来实现对整个图像和新颖视图图像的编辑。然而,编辑仅限于2D图像,无法更改对象的空间位置,更不用说更改对象的形状。ObjectNeRF具有分解架构,只能复制、移动或旋转对象。然而,我们的框架支持在NeRF中编辑对象的几何形状,然后可用于合成照片真实感的新视图图像以进行可视化。
2.2.3D编辑方法
编辑3D模型意味着在用户给定的一些控制下变形3D模型的形状。关于显式几何表示的编辑已经有很多工作。传统网格变形方法基于拉普拉斯坐标、泊松方程和双拉普拉斯座标。作为其中的代表性工作,ARAP(As-Rigid-As-Possible)变形是一种交互式网格编辑方案,通过保持局部变换的刚性,在变形过程中保留细节。驱动网格变形的另一种方法是通过代理,如骨架(skeletons)或笼(cages)。这些方法需要计算代理和网格顶点之间的权重,并将代理的变换传播到网格。随着几何模型的激增,数据驱动变形变得可用,它分析数据集中现有形状的变形先验,并产生更真实的结果。同时,大量数据还允许将神经网络引入3D编辑。除了显式网格表示之外,还可以结合神经网络编辑隐式场。Deng等人提出了变形隐式场(deformed implicit field),该场能够基于对象类别的学习信息建模密集曲面对应的形状编辑。我们的工作还旨在编辑隐式表示,特别是NERF。不同之处在于,我们利用了显式网格编辑的直观和方便性。通过建立显式网格表示和隐式神经表示之间的联系,我们使用成熟的网格变形方法编辑隐式表示的几何体。
3.方法
我们的工作基于神经辐射场(NeRF),它在新视图合成中具有很好的性能。我们的方法使用户能够对场景内容执行形状变形,并可以在编辑后从任意视图生成新图像。我们将首先简要回顾 NeRF 管道(第 3.1 节),然后介绍如何从场景的隐式表示中提取显式三角形网格表示,并使用户能够编辑网格表示(第 3.2 节)。
用户编辑场景的三角形网格表示后,我们需要将此变形转换为隐式体积表示(implicit volume representation)。我们将转换分为两个步骤。第一步是将曲面网格变形转换为体积网格(volumetric mesh),在其中我们构建了一个四面体网格(tetrahedra mesh),该网格围绕曲面网格(surface mesh),并将用户对曲面网格的编辑转换为四面体网格上的离散变形场(第3.3节)。下一步是将离散变形场变换为空间体积中的连续变形场,该变形场用于引导光线弯曲,以呈现符合用户编辑的图像(第3.4节)。
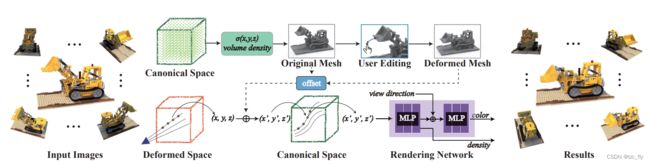
我们的方法建立了显式网格表示和隐式辐射场之间的联系,使用户能够通过直观编辑修改辐射场的几何体。方法pipeline如图2所示。
- 图2:NeRF Editing框架的pipeline。用户编辑重建的网格,并构建连续变形场以相应地弯曲光线。(Canonical space为变形前的空间,Deformed space为变形后的空间)
3.1.神经辐射场
神经辐射场NeRF提出使用多层感知器(MLP)网络从稀疏图像集建模场景的几何结构和外观。给定已知的摄像机参数,可以将每个图像的像素坐标变换到世界坐标系并与摄像机位置连接,以生成指向场景的光线(回顾NeRF数据预处理概述)。NeRF对光线上的点进行采样,并使用体渲染(volume rendering)获得每条光线积累到像素上的颜色。每个采样点的空间坐标 p = ( x , y , z ) p=(x,y,z) p=(x,y,z)和光线方向 d = ( θ , φ ) d=(\theta,φ) d=(θ,φ)将通过位置编码 ζ ( ⋅ ) ζ(·) ζ(⋅),然后输入全连接网络以预测体积密度 σ \sigma σ和RGB值 c c c( F Θ : ( ζ ( p ) , ζ ( d ) ) → ( σ , c ) F_{Θ}:(ζ(p),ζ(d))\rightarrow(\sigma,c) FΘ:(ζ(p),ζ(d))→(σ,c),其中 Θ Θ Θ代表全连接网络的参数)。预测密度值 σ \sigma σ可以解释为射线在采样点终止的可微概率,并且对应于射线 r ( t ) r(t) r(t)的图像像素的颜色 C ^ ( r ) \widehat{C}(r) C (r)可以通过离散积分来计算: C ^ ( r ) = ∑ i = 1 N e x p ( − ∑ j = 1 i − 1 σ j δ j ) ( 1 − e x p ( − σ i δ i ) ) c i \widehat{C}(r)=\sum_{i=1}^{N}exp(-\sum_{j=1}^{i-1}\sigma_{j}\delta_{j})(1-exp(-\sigma_{i}\delta{i}))c_{i} C (r)=i=1∑Nexp(−j=1∑i−1σjδj)(1−exp(−σiδi))ci其中, δ i = t i + 1 − t i \delta_{i}=t_{i+1}-t_{i} δi=ti+1−ti是相邻样本之间的距离。该网络由RGB损失函数监督,该函数是在生成的颜色 C ^ ( r ) \widehat{C}(r) C (r)和GT的颜色 C ( r ) C(r) C(r)之间计算的。
3.2.显式曲面网格表示的编辑
训练 NeRF 网络后,可以使用 Marching Cubes 直接从神经辐射场中提取显式三角形网格表示。然而,从原始NeRF网络提取的网格通常具有粗糙表面。为了获得满意的网格表示,我们采用NeuS中提出的重建方法,该方法采用无偏差体绘制方式(bias-free volume rendering),将几何体学习为神经符号距离函数(SDF,signed distance function)表示。从SDF的 zero-level set 提取的网格表示将用作用户的编辑对象,允许用户直观地编辑场景内容。在本文中,我们使用经典的ARAP(as-rigid-as-possible)变形方法,使用户能够交互变形网格。应注意,这里可以使用任何其他网格变形方法,包括基于skeleton和基于cage的方法。
提取的三角形网格表示为 S S S, N ( i ) N(i) N(i)代表节点 i i i相邻的节点集合。我们进一步将 v i ∈ R 3 v_{i}\in R^{3} vi∈R3表示为节点 i i i在网格 S S S上的位置。在用户编辑后,网格 S S S被变换为具有相同连接性和不同节点位置 v i ′ v_{i}' vi′的变形网格 S ′ S' S′(deformed mesh)。整体ARAP的变形能量(deformation energy)用于测量整个网格的刚度,是每个变形单元的变形能量之和,包括节点 i i i及其1阶邻居,如下所示: E ( S ′ ) = ∑ i = 1 n ∑ j ∈ N ( i ) w i j ∣ ∣ ( v i ′ − v j ′ ) − R i ( v i − v j ) ∣ ∣ 2 E(S')=\sum_{i=1}^{n}\sum_{j\in N(i)}w_{ij}||(v_{i}'-v_{j}')-R_{i}(v_{i}-v_{j})||^{2} E(S′)=i=1∑nj∈N(i)∑wij∣∣(vi′−vj′)−Ri(vi−vj)∣∣2其中, w i j = 1 2 ( c o t α i j + c o t β i j ) w_{ij}=\frac{1}{2}(cot\alpha_{ij}+cot\beta_{ij}) wij=21(cotαij+cotβij)是cotangent权重, α i j , β i j \alpha_{ij},\beta_{ij} αij,βij是与网格edge ( i , j ) (i,j) (i,j)相反的角度。 R i R_{i} Ri是顶点 i i i处的局部旋转。变形形状 S ′ S' S′通过使得ARAP能量最小化获得,该ARAP能量可以通过交替优化局部旋转 R i R_{i} Ri和变形位置 v i ′ v_{i}' vi′有效求解。
3.3.变形转换到离散体积(Discrete Volume)
用户编辑场景的三角形网格表示后,需要将变形转换为隐式体积表示(volume representation)。如前所述,我们将转换分为两个步骤。第一步,我们建立一个四面体网格(tetrahedral mesh,一种离散的体积表示方法)去覆盖提取的三角网格。从提取的三角形网格 S S S开始,我们首先计算包裹网格 S S S的笼形网格(cage mesh)。这可以通过在法线方向上从网格表面偏移一定距离来扩大三角形网格来实现。我们将默认值设置为从相机位置到对象中心的平均距离的5%。cage mesh的内部空间可以视为隐式体积的 “有效空间(effective space)”,因为场景的真实几何曲面附近的区域由该笼状网格包围。编辑具有多个对象的较大场景时,此设计还确保未编辑的其他对象不受影响。我们使用四面体化方法(tetrahedralization method),Tetwield,对笼形网格进行四面体化,以获得四面体网格表示 T T T。应注意的是,提取的三角形网格 S S S也包裹在四面体网格 T T T中。补充材料中可视化了一些提取的三角网格 S S S和相应的四面体网格(由四面体堆积组成的3D对象)。

- 补充材料:三角网格和四面体网格
我们使用三角网格节点 v i v_{i} vi的位移来驱动四面体网格 T T T的变形,这将surface deformation转换到四面体网格。变形的四面体网格表示为 T ′ T' T′, t k t_{k} tk和 t k ′ t_{k}' tk′分别表示变形前后的四面体网格的节点,其中 k k k是节点的索引。在这里,我们还使用 ARAP 变形方法在surface mesh变形约束下对四面体网格 T T T 进行变形。3.2节中的公式可以从三角形网格直接扩展到四面体网格。我们可以找到每个三角形网格顶点所在的四面体,并计算其相对于四面体四个顶点的重心坐标。优化问题变成: m i n E ( T ′ ) , s u b j e c t . t o . A t ′ = v ′ minE(T'),subject.to.At'=v' minE(T′),subject.to.At′=v′其中, A A A是重心权重矩阵。该优化问题可以使用拉格朗日乘子法转化为线性方程组。
3.4.光线弯曲
将表面变形转换到四面体网格后,我们可以得到“有效空间”的离散变形场。我们现在使用这些离散变换来弯曲光线。为了生成变形辐射场的图像(deformed radiance field),我们将光线投射到包含变形四面体网格的空间。对于射线上的每个采样点,我们找到它位于变形四面体网格 T ′ T' T′中的哪个四面体。使用 T T T和 T ′ T' T′之间的对应关系,可以获得从变形后的节点到变形前的节点的位移。通过对采样点所在四面体的四个节点的位移进行重心插值,采样点的位移返回到原始“有效空间”对比可以获得 ∆ p ∆p ∆p。我们加上位移 ∆ p ∆p ∆p转换为采样点的输入坐标,以预测密度和RGB值。 ( ζ ( p + ∆ p ) , ζ ( d ) ) → ( σ , c ) (ζ (p+∆p),ζ(d))\rightarrow(\sigma,c) (ζ(p+∆p),ζ(d))→(σ,c)沿射线的采样点的密度和RGB值用于3.1节中的公式计算相应的像素颜色。应注意,不在四面体网格 T ′ T' T′内的采样点将不会移动,即,四面体网格外的光线部分将不会弯曲。构建变形场的过程如图3所示。

图3:使用用户指定的离散变形来弯曲光线。
4.实验
4.1.数据集和metrics
Nerf-Editing 在几个公共合成数据上展示了结果,包括 mixamo 、乐高推土机和 NeRF 中的椅子。 此外,还在 FVS 数据集中真实捕获的马雕像和我们自己捕获的几个真实场景上测试了方法。mixamo中的角色是我们自己绘制的。我们使用Blender从上半球生成100个随机视图用于训练。对于来自NeRF数据集的数据,我们使用数据集的默认训练设置。对于自己拍摄的真实场景,我们留下一张图片进行验证,其他图片用于训练。
需要注意的是,与 dynamic NeRF 方法不同,在用户编辑后,很难获得新视图合成结果的ground truth,特别是在真实场景上,因为这样的编辑场景实际上并不存在。因此,我们主要对mixamo中的特征进行定量和定性评估。具体而言,我们装配mixamo角色模型,将变形角色渲染为ground truth,并将其与NeRF编辑方法的输出进行比较。我们使用结构相似性指数度量(SSIM,Structural Similarity Index Measure)、学习的感知图像块相似性(LPIPS,Learned Perceptual Image Patch Similarity)和峰值信噪比(PSNR,Peak Signal-to-Noise Ratio)作为评估方法性能的指标。我们还评估真实场景中的Fréchet初始距离(FID,Fréchet Inception Distance)分数,以衡量编辑前和编辑后结果之间的相似性,因为ground truth并非不可或缺。
4.2.实验结果
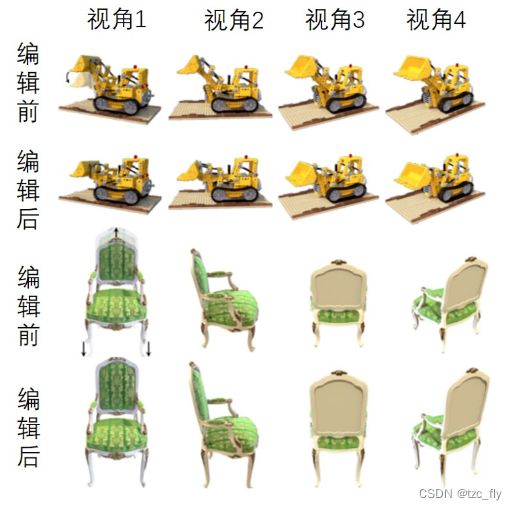
- 图4:展示了所提出方法在合成场景上的编辑结果;前两行展示了在乐高推土机模型上几何变形的结果,用户可以将推土机的铲子放下,实现了对复杂合成数据的编辑;后两行展示了对椅子模型变形编辑的结果,用户可以拉伸椅子的靠背和腿,实现对物体局部部件的编辑。
- 图5:NeRF editing框架(行“Edit1”、“Edit2”、“Edit3”)的结果与真实捕获的长颈鹿软玩具上的原始NeRF结果(行“Before”)进行了比较。不同的列显示不同的视图。我们可以将对象编辑成不同的姿势,并在不同的视图下进行渲染。“Edit Op”表示“编辑操作”。
- 图6:NeRF editing框架(行“After”)的结果与多个实际捕获数据的原始NeRF结果(行“Before”)进行比较。不同的列显示不同的视图。我们编辑静态神经辐射场,并在不同视图下显示变形结果。
注意,该研究设计了两种直接的baseline方法进行对比,以证明提出方法的优越性:
- 第一种是在弯曲光线时,直接选用最近邻的网格顶点位移作为该采样点的位移,记为Closest Point;
- 第二种选取了采样点最近邻的三个网格顶点,以距离的倒数作为系数线性插值得到位移,记为3NN。
- 图7:展示了与baseline方法的对比,前两行是在mixamo的合成数据上进行的编辑,变形后的物体 (GT) 可以通过对原模型变形得到。第三行是在真实拍摄物体上进行的编辑,变形后的GT不存在,所以使用NeRF的渲染结果作为代替。与Closest Point和3NN基线进行视觉比较。Closest Point和3NN可能会导致不连续,因此生成的渲染结果具有明显的伪影。
- 表1:与Closest Point和3NN基线进行定量比较。可以看出,Nerf-editing框架取得了更好的结果。注意,前三个指标是根据mixamo合成数据计算的,而最后一个FID是根据实际数据计算的。