DQN（deep Q-network）算法简述

本文通过整理李宏毅老师的机器学习教程的内容，简要介绍深度强化学习（deep reinforcement learning）中的 DQN（deep Q-network）算法。

李宏毅老师课程的B站链接：
李宏毅, 深度强化学习, Q-learning, basic idea
李宏毅, 深度强化学习, Q-learning, advanced tips
李宏毅, 深度强化学习, Q-learning, continuous action

相关笔记：
策略梯度法（policy gradient）算法简述
近端策略优化（proximal policy optimization）算法简述
actor-critic 相关算法简述

1. 基本概念

DQN 是基于价值（value-based）而非策略（policy-based）的方法，学习的不是策略，而是一个评论家（critic）。critic 并不直接采取行为，而是评价行为的好坏。

1.1 状态价值函数（state value function）

有一种 critic 叫做状态价值函数（state value function）$V^{\pi }(s)$，即以一个策略 $\pi$ 与环境做互动，当处于某一状态 $s$ 时，接下来直到游戏结束的累计激励的期望值。当策略不同时，即使状态相同，得到的激励也是不一样的，$V^{\pi }(s)$ 就不一样。

此外，由于无法列举所有的状态，因此 $V^{\pi }(s)$ 实际上是一个网络，在训练时也就是一个回归（regression）问题。

具体地，衡量状态价值函数有两种不同的方法：基于蒙特卡洛的方法（Monte-Carlo based approach, MC）和基于时序差分的方法（temporal-difference approach, TD）。

基于蒙特卡洛的方法即是让 actor 与环境做互动，优化目标为，使各状态的 $V^{\pi }(s)$ 与后续累计激励 $G_s$ 尽可能接近。

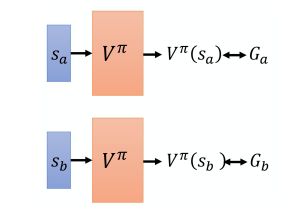
但是基于蒙特卡洛的方法在每次更新网络时，都需要把游戏玩到结束，但有些游戏的时间比较长，因此会采用基于时序差分的方法。该方法不需要把游戏玩到底，而是通过时序差分的方式，使相邻状态下的价值函数之差与前一状态的激励尽可能接近：

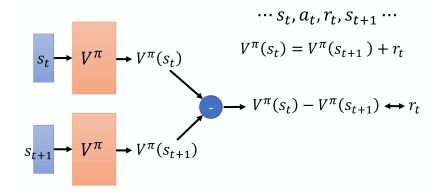
由于游戏本身可能具有随机性，激励即为随机变量，其方差会对算法效果产生影响。基于蒙特卡洛的方法由于使用累计激励 $G_s$，方差会很大；而基于时序差分的方法使用单步激励 $r_t$，方差比较小，但是会遇到一个问题就是 $V^{\pi }(s_{t+1})$ 可能估计不准，也会影响学习结果。实际上，基于时序差分的方法比较常用，而基于蒙特卡洛的方法较少见。

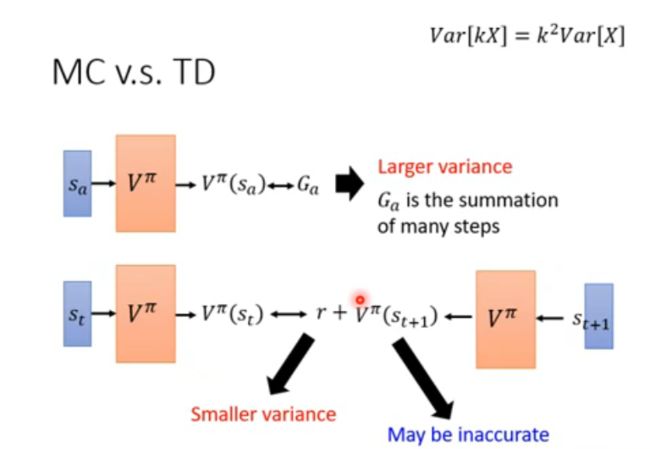
此外，两种方法产生的估计结果也可能不同，举例说明：

在上例中，当状态 $s_a$ 产生 $s_b$ 不是巧合时，即 $s_a$ 影响了 $s_b$，看到 $s_a$ 之后 $s_b$ 就会得不到激励，则基于蒙特卡洛的方法合理；而如果状态 $s_a$ 产生 $s_b$ 只是巧合，则基于时序差分的方法合理。

1.2 状态-动作价值函数（state-action value function, Q function）

另一种 critic 叫做状态-动作价值函数（state-action value function），也叫 Q 函数，即在某一状态 $s$ 采取某一动作 $a$，假设一直使用同一个策略 $\pi$，得到的累计激励的期望值。

需要注意的是，对于策略 $\pi$ 来说，在状态 $s$ 不一定采取动作 $a$，但 Q 函数可以强制其采取动作 $a$，而后续仍使用策略 $\pi$ 继续进行，即 $Q^{\pi }(s,a)$。具体地，Q 函数有两种写法：

只要有了 Q 函数，就可以做强化学习了，流程图如下：

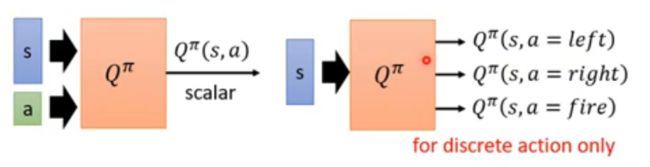
其中：
$${\pi }^{\prime }(s)=\arg \underset{a}{\max }{Q}^{\pi }(s,a)$$

所以，实际上并没有一个所谓的策略 ${\pi }^{\prime }$，${\pi }^{\prime }$ 是由 Q 函数推出来的。

下面证明为什么由 Q 函数推出来的 ${\pi }^{\prime }$ 比 $\pi$ 要好。

所谓的好，即是对所有状态而言，状态价值函数都更大，具体推导如下：
$$\begin{gathered} V^{\pi }(s)=Q^{\pi }(s,\pi (s))\le \underset{a}{\max }{Q}^{\pi }(s,a)=Q^{\pi }(s,{\pi }^{\prime }(s)) \\ {V}^{\pi }(s)\le Q^{\pi }(s,{\pi }^{\prime }(s))=E[r_t+V^{\pi }(s_{t+1})|s_t=s,a_t={\pi }^{\prime }(s_t)]\le E[r_t+Q^{\pi }(s_{t+1},{\pi }^{\prime }(s_{t+1}))|s_t=s,a_t={\pi }^{\prime }(s_t)]=E[r_t+r_{t+1}+V^{\pi }(s_{t+2})|...]\le E[r_t+r_{t+1}+Q^{\pi }(s_{t+2},{\pi }^{\prime }(s_{t+2}))|...]=...\le V^{{\pi }^{\prime }}(s) \end{gathered}$$

1.3 训练技巧

下面介绍几个 DQN 中一定会用到的技巧。

1.3.1 目标网络（target network）

第一个技巧是目标网络（target network）。

根据 Q 函数：
$$Q^{\pi }(s_t,a_t)=r_t+Q^{\pi }(s_{t+1},\pi (s_{t+1}))$$

其中，等号左侧是网络的输出，右侧是目标，但是由于目标中含有 Q 函数，因此目标一直在变，会给训练带来困难。

解决办法是把其中一个 Q 网络（通常是等号右侧的目标网络）固定住，最小化模型输出与目标之间的均方误差（mean square error），当等号左侧的 Q 网络更新过几次之后，再用更新过的 Q 网络去替换目标网络，继续迭代。如下图所示：

1.3.2 探索（exploration）

第二个技巧是探索（exploration）。

如果在某一状态下，所有动作均未被采取过，此时采取某个动作得到了正向的激励，会导致后续出现此状态时只采取这个动作，而不去探索其他的动作：

这个问题就是探索-利用窘境（exploration-exploitation dilemma）问题。

解决方法有两种：$ϵ$ 贪心（epsilon greedy）和玻尔兹曼探索（Boltzmann exploration）。

$ϵ$ 贪心方法如下：

玻尔兹曼探索的公式如下：
$$P(a|s)=\frac{e^{Q(s,a)}}{{\sum }_a{e}^{Q(s,a)}}$$

该方法有点像策略梯度，即根据 Q 函数定一个动作的概率分布。Q 值越大，采取该动作的概率越高，而指数运算使得概率不会为 0，即对于 Q 值小的动作也不代表不能尝试。

1.3.3 经验回放（experience replay）

第三个技巧是经验回放（experience replay），如下图所示：

经验回放有两个好处：

其一，实际在做强化学习时，往往最耗时的步骤是与环境做互动，训练网络反而是比较快的（用 GPU 训练其实很快）。用回放缓存区可以减少与环境做互动的次数，因为在训练时，经验不需要全部来自于某一个策略。一些过去的策略所得到的经验可以放在缓存区里被使用很多次，这样的采样利用率是比较高效的。

其二，在训练网络时，我们希望一个批次里面的数据越多样越好。如果数据都是同样性质的，性能会比较差。如果数据缓存区里面的经验来自于不同的策略，容易满足多样性。

这里指的说明的是，缓存区中的经验数据，即便使用的策略 $\pi$ 与当前策略不同，也没有影响。原因是，我们每次迭代所使用的采样经验是基于一个状态，而不是一个轨迹（trajectory），所以不受 off-policy 的影响。

1.4 算法流程

2. 进阶技巧

2.1 double DQN

在原始 DQN 算法中，由于网络存在误差，被高估的动作会被反复选择，因此 Q 值经常被高估。

为了解决这个问题，可同时使用两个网络，一个网络 $Q$ 用于更新参数选择动作，另一个固定不动的网络 $Q^{\prime }$ 用作目标网络计算 Q 值，即为 double DQN：
$$Q(s_t,a_t)=r_t+Q^{\prime }(s_{t+1},\arg \underset{a}{\max }Q(s_{t+1},a))$$

参考文献：
Hado V. Hasselt, “Double Q-learning”, NIPS 2010
Hado V. Hasselt, Arthur Guez, David Silver, “Deep Reinforcement Learning with Double Q-learning”, AAAI 2016

2.2 dueling DQN

dueling DQN 与原始 DQN 唯一的差别，是改变了网络的架构：

改变架构的好处：有时可以通过更新 $V(s)$ 而非 $A(s,a)$ 即可达到效果
为了让网络倾向于更新 $V(s)$ 而不是 $A(s,a)$，可以对 $A(s,a)$ 加一些约束。

参考文献：
Ziyu Wang, Tom Schaul, Matteo Hessel, Hado van Hasselt, Marc Lanctot, Nando de Freitas, “Dueling Network Architectures for Deep Reinforcement Learning”, arXiv preprint, 2015

2.3 优先经验回放（prioritized replay）

对于输出与目标之间差距较大的训练数据，设置较大的被采样概率，即优先权（priority）。

实际在做 prioritized replay 时，不仅会改变采样的过程，还会因为改变采样过程而改变更新参数的方法。所以它不只是改变了采样数据的分布，还改变了训练过程。

参考文献：
Prioritized Experience Replay

2.4 多步采样（multi-step）

通过连续多步的采样，可以在基于蒙特卡洛的方法和基于时序差分的方法间取得平衡：
$$Q(s_t,a_t)=\sum _{t^{\prime }=t}^{t+N}{r}_{t^{\prime }}+\hat{Q}(s_{t+N+1},a_{t+N+1})$$

2.5 噪声网络（noisy net）

如前所述，$ϵ$ 贪心探索相当于在动作空间加噪声，但有一个更好的方法叫做 noisy net，是在参数空间加噪声。它是指，每次在一个回合（episode）开始时，在Q 网络的每个参数上面加上一个高斯噪声（Gaussian noise），就把原来的 Q 函数变成 $\tilde{Q}$ :
$$a=\arg \underset{a}{\max }\tilde{Q}(s,a)$$

这里需要注意的是，噪声在一个回合内是不会改变的。

OpenAI 和 DeepMind 在同一时间提出了一模一样的方法，并且都发表在 ICLR 2018 会议中，区别在于，OpenAI 的方法是把每个参数直接加了一个高斯噪声；DeepMind 的方法比较复杂，噪声由一组参数控制，网络可以自己决定噪声的大小。

在参数空间加噪声的好处是，可以保证在相同状态下输出相同的动作，即依赖状态的探索（state-dependent exploration）。

参考文献：
Parameter Space Noise for Exploration, OpenAI
Noisy Networks for Exploration, DeepMind

2.6 分布式 Q 函数（distributional Q-function）

由于 Q 函数是累积激励的期望值，而相同的期望可能对应不同的分布，所以对分布进行建模更合理。

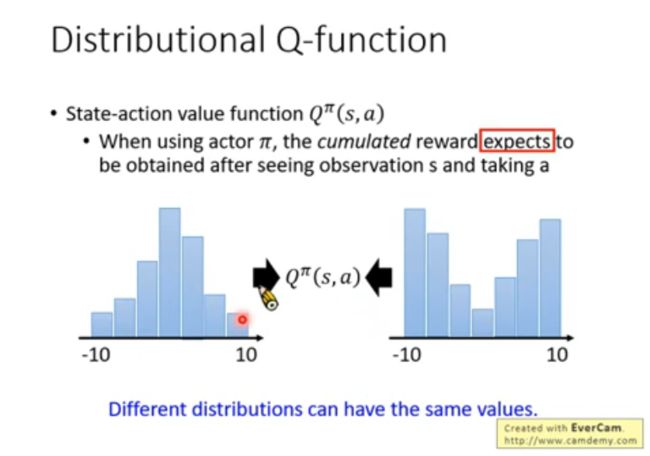
具体做法是，把分布的值对应到某个范围，输出范围内每个值的概率：

虽然实际在测试时，仍然选择平均值最大的动作执行，但其实可以有其他方法，例如在两个动作的平均值相近的情况下，选择一个风险较小的动作来执行。

该方法不易实现。

2.7 rainbow

最后一个技巧叫做彩虹（rainbow），即假设上述每种方法对应一种颜色，把所有方法综合起来，就变成彩虹。
（实际上前面只有 6 种技巧。）

可以对比 rainbow 和各种单一方法的效果，其中得分取中位数是为了防止波动过大：
（注：这里有 A3C 但没有单纯的 multi-step）

也可以在 rainbow 中去掉一种方法，对比各算法效果：

这里可以看出，去掉 double DQN 影响不大，在论文中的解释是，当有使用 distributional Q-function 时，通常就不会高估激励，反而可能由于限制范围的原因造成低估。

参考文献：
Rainbow: Combining Improvements in Deep Reinforcement Learning

3. 连续动作的场景

DQN 其实存在一些问题，最大的问题就是不容易处理连续动作。

如前所述，每次选取动作时须使 $Q$ 值最大：
$$a=\arg \underset{a}{\max }Q(s,a)$$

解决方案有如下四种：

第一个方案，可以采样出 $N$ 个可能的动作 $\{a_1,a_2,...,a_n\}$，代入 $Q$ 函数中，取 $Q$ 值最大的动作。

第二个方案，既然要解的是一个优化（optimization）问题，可以使用梯度上升法（gradient ascent），但是这意味着每次选择动作时还要训练一次网络，因此运算量很大。

第三个方案，设计一个网络架构，使得 $Q$ 函数的最大化变得容易：

其中，$\sum$ 矩阵一定是正定的。于是，$(a-\mu (s){)}^T\sum (s)(a-\mu (s))$ 的值越小，最终的 $Q$ 值就越大。论文中有介绍保证 $\sum$ 矩阵是正定的方法。

第四个方案，就是不使用 DQN 了。可以考虑将基于策略（policy）的方法 PPO 和基于价值（value）的方法 DQN 结合在一起，得到 actor-critic 的方法：