DQN算法的原理与复现
基本思路
先来解释下Q-learning
简单来说就是瞬时奖励+记忆经验奖励。
瞬时奖励:做了一个动作就能获得的奖励
经验奖励:按照训练时的经验,上一系列动作发生之后,接下来怎么做才能获得更大的奖励,换句话就是说根据复盘经验去研究如何更好地补刀,从而形成一系列的动作(连招)
DQN自然就是加入深度神经网络进行预测,我们先来看看Q-learning是如何运行的
1收集数据(即游戏记录)

2令目标等于以下公式(获得价值最高的选择):

3目标函数(获得最小的误差)

整体流程

伽马值(就是那个很像r的)用于减少下一步的贡献度,因为下一步与上一步紧密相连,故不能减少太多,我们也是将其设置为0.99
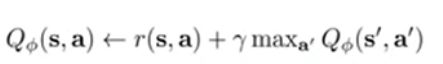
因为其是瞬时奖励,加的是记忆中价值量最大的动作,但也终归是记忆中的,我们要对其影响做一个削弱,构成一个估计值
举个通俗的例子,走迷宫
状态0,1,2,3,4,5,其中5是出口
目标就是能走出去
并非每个状态都是互通的(比如2到3)
通过不断地迭代让智能体逃出去
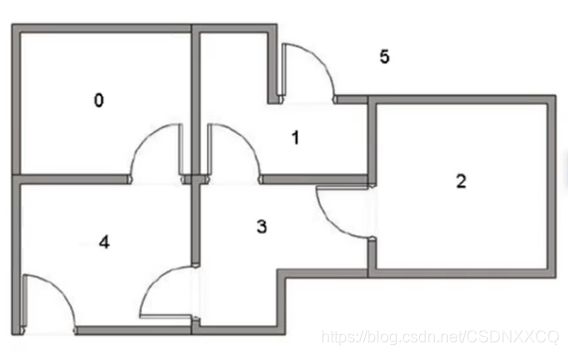
5是出口我们就直接把运行到状态5的奖励设为100,其余为0

数据的格式
对R与Q进行初始化
Q是一个由0构成的没有实际意义的空表,要不断地进行填充
行为state,列为action

-1表示此路不通,只要没到5,奖励都为0
开始迭代
假设初始化状态为1
根据右表action只能选择3和5
此时选择3还是5呢,当前的Q为空表,按理来说是要比较这两个选择的价值的,但是我们是从0开始训练,故我们只能先随机选一个,比如5
接下来就到了状态5,此时有三种选择,1,4,5,选哪个呢
![]()
![]()
其中0.8是伽马值,就是折扣因子,相当于经验记忆奖励的权重,然后由此我们就得到了Q(1,5),5亦代表了游戏结束
如此重复,尽可能地把每个可能性都试一遍,这也是为什么次数越多模型的准确度越高的原因,联想一波蒙特卡洛即可。
那么我们想一下,如果放到游戏画面,我们真的能做到穷举吗,那个像素点太多了,Q(s,a)就不能用表格来表达了,于是我们想到了用神经网络去表达,现在一般的方法是构建一个 replay buffers 到时候去里面取一个batch就行,其实就是off policy策略,这个策略的代码构建还是比较容易的,
第一种改进,double-dqn

红色为目标,蓝色为模型达到的程度
换句话说就是模型高估了自己

为了提升模型效果,我们在原来训练的基础上再用另一个神经网络训练一次
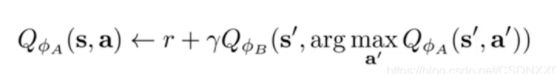
注意,里面的括号下方的小A与小B都代表一个神经网络
第二种改进,dueling-dqn
在同一个网络中分别嫁接两个全连接层,以此为原理使得网络能同时更新相同state下不同的行为(action)可能导致的结果

![]()
也就是说其实只有V(s)是变量用于微调
mulit-step-dqn策略
就像下围棋一样,
不光要看眼前的下一步,也要看下N步的结果,该算法就是在计算Q值得时候选择多个时间步
只看下一步
![]()
只看下N步
![]()
联想下梯度下降中的随机/批量,这个就是小批量
连续值的处理方法-连续动作
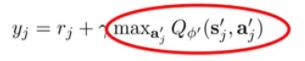
这就是一个求极值的问题,常用的解法有采样,梯度上升
不断地运行,并比较,选择一个最大值就可以了

问题来了,这样子不断地运算,动作越多计算的负担越大,于是我们要优化计算方法,改变数据的输入格式
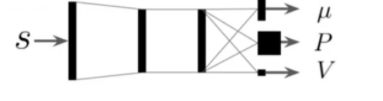
即重新定义Q网络,输出三个结果分别是向量,矩阵,值
由此构成新的公式

![]()
这个是恒为正的,
![]()
此时代入Q(s,a)即可得出
![]()
部分代码复现
训练网络
while True:
env.render()
action = RL.choose_action(observation)#根据状态选择行动
observation_,reward,done = env.step(action)#定义更新环境
RL.store_transition(observation,action,reward,observation_)
if (step>x) and (step%y== 0):#一定的次数后学习
RL.learn()
observation = observation_
if done:
break
step += 1
行动参数更新
def choose_action(self,observation):
observation = observation[np.newaxis,:]
if np.random.uniform() < self.epsilon:
actions_value = self.sess.run(self.q_eval,feed_dict = {self.s:observation})
action = np.argmax(actions_value)#选择最高价值的行动
else:
action = np.random.randint(0,self.n_actions)
return action
经验池
def store_transition(self,s,a,r,s_):
if not hasattr(self,'memory_counter'):
self.memory_counter = 0#计数器
transition = np.hstack(s,[a,r],s_)
index = self.memory_counter%self.memory_size#样本数量超过经验池大小时开始覆盖
self.memory[index,:] = transition
self.memory_counter += 1
学习函数
#学习函数
def leran(self):
q_traget = q_eval.copy()
batch_index = np.arange(self.batch_size,dtype = np.int32)
eval_act_index = batch_memory[:,self.n_fextures].astype(int)
reward = batch_memory[;self.n_fextures +1]
q_traget[batch_index,eval_act_index] = reward + self.gamma * np.max(q_next,axis = 1)
-,self.cost = self.sess.run([self._train_op,self.loss],feed_dict = {self.s:batch_memory[:,:self.n_fextures],self.q_traget:q_traget})
self.cost_his.append(self.cost)
网络搭建
def _build_net(self):
#----------------构建评估网络------------------
self.s = tf.placeholder(tf.float32, [None, self.n_features], name='s') # 输入
self.q_target = tf.placeholder(tf.float32, [None, self.n_actions], name='Q_target') #计算loss
with tf.variable_scope('eval_net'):
# c_names(collections_names) )是存储变量的集合
c_names, n_l1, w_initializer, b_initializer = \
['eval_net_params', tf.GraphKeys.GLOBAL_VARIABLES], 10, \
tf.random_normal_initializer(0., 0.3), tf.constant_initializer(0.1) #网络层的参数
# 第一层。稍后分配给目标网络时使用集合
with tf.variable_scope('l1'):
w1 = tf.get_variable('w1', [self.n_features, n_l1], initializer=w_initializer, collections=c_names)
b1 = tf.get_variable('b1', [1, n_l1], initializer=b_initializer, collections=c_names)
l1 = tf.nn.relu(tf.matmul(self.s, w1) + b1)
# 第二层。稍后分配给目标网络时使用集合
with tf.variable_scope('l2'):
w2 = tf.get_variable('w2', [n_l1, self.n_actions], initializer=w_initializer, collections=c_names)
b2 = tf.get_variable('b2', [1, self.n_actions], initializer=b_initializer, collections=c_names)
self.q_eval = tf.matmul(l1, w2) + b2
with tf.variable_scope('loss'):
self.loss = tf.reduce_mean(tf.squared_difference(self.q_target, self.q_eval))
with tf.variable_scope('train'):
self._train_op = tf.train.RMSPropOptimizer(self.lr).minimize(self.loss)
# ------------------ 构建目标网络 ------------------
self.s_ = tf.placeholder(tf.float32, [None, self.n_features], name='s_') # input
with tf.variable_scope('target_net'):
# c_names(collections_names) 是存储变量的集合
c_names = ['target_net_params', tf.GraphKeys.GLOBAL_VARIABLES]
# 第一层。稍后分配给目标网络时使用集合
with tf.variable_scope('l1'):
w1 = tf.get_variable('w1', [self.n_features, n_l1], initializer=w_initializer, collections=c_names)
b1 = tf.get_variable('b1', [1, n_l1], initializer=b_initializer, collections=c_names)
l1 = tf.nn.relu(tf.matmul(self.s_, w1) + b1)
# 第二层。稍后分配给目标网络时使用集合
with tf.variable_scope('l2'):
w2 = tf.get_variable('w2', [n_l1, self.n_actions], initializer=w_initializer, collections=c_names)
b2 = tf.get_variable('b2', [1, self.n_actions], initializer=b_initializer, collections=c_names)
self.q_next = tf.matmul(l1, w2) + b2



