近端策略优化(proximal policy optimization)算法简述
本文通过整理李宏毅老师的机器学习教程的内容,简要介绍深度强化学习(deep reinforcement learning)中的近端策略优化算法(proximal policy optimization)。
李宏毅老师课程的B站链接:
李宏毅, 深度强化学习, proximal policy optimization
相关笔记:
策略梯度法(policy gradient)算法简述
DQN(deep Q-network)算法简述
actor-critic 相关算法简述
PPO 是策略梯度法的一个变形,它是 OpenAI 现在默认的强化学习算法。
PPO, paper
与原始策略梯度法不同的是,PPO 是 off-policy 算法(原始策略梯度法是 on-policy 算法):

首先介绍 重要性采样(importance sampling) 的概念:
假设 x x x 是从分布 p p p 中采样出来,则:
E x ∼ p [ f ( x ) ] = ∫ f ( x ) p ( x ) d x ≈ 1 N ∑ i = 1 N f ( x i ) E_{x \sim p}[f(x)] = \int f(x) p(x) dx \approx \frac{1}{N} \sum_{i=1}^{N} f(x^i) Ex∼p[f(x)]=∫f(x)p(x)dx≈N1i=1∑Nf(xi)
当无法从分布 p p p 采样数据,只能从另一个分布 q q q 采样数据时:
E x ∼ p [ f ( x ) ] = ∫ f ( x ) p ( x ) d x = ∫ f ( x ) p ( x ) q ( x ) q ( x ) d x = E x ∼ q [ f ( x ) p ( x ) q ( x ) ] E_{x \sim p}[f(x)] = \int f(x) p(x) dx = \int f(x) \frac{p(x)}{q(x)} q(x) dx = E_{x \sim q}[f(x) \frac{p(x)}{q(x)}] Ex∼p[f(x)]=∫f(x)p(x)dx=∫f(x)q(x)p(x)q(x)dx=Ex∼q[f(x)q(x)p(x)]
即,用 q q q 代替 p p p 采样,需要乘上一个重要性权重(importance weight) p ( x ) q ( x ) \frac{p(x)}{q(x)} q(x)p(x) 来修正两个分布之间的差异。理论上 q q q 可以是任何分布,唯一的限制是当 q ( x ) q(x) q(x) 为 0 0 0 时, p ( x ) p(x) p(x) 也要为 0 0 0,否则会没有定义。
虽然可以把 p p p 换成任何 q q q,但是在实现上,两者不能差太多,否则会有一些问题。因为虽然 f ( x ) f(x) f(x) 和 f ( x ) p ( x ) q ( x ) f(x) \frac{p(x)}{q(x)} f(x)q(x)p(x) 的期望相同,但是方差不同:
D x ∼ p [ f ( x ) ] = E x ∼ p [ f ( x ) 2 ] − ( E x ∼ p [ f ( x ) ] ) 2 D_{x \sim p}[f(x)] = E_{x \sim p}[f(x) ^ 2] - (E_{x \sim p}[f(x)]) ^ 2 Dx∼p[f(x)]=Ex∼p[f(x)2]−(Ex∼p[f(x)])2
D x ∼ q [ f ( x ) p ( x ) q ( x ) ] = E x ∼ q [ ( f ( x ) p ( x ) q ( x ) ) 2 ] − ( E x ∼ q [ ( f ( x ) p ( x ) q ( x ) ) ] ) 2 = E x ∼ p [ f ( x ) 2 p ( x ) q ( x ) ] − ( E x ∼ p [ f ( x ) ] ) 2 D_{x \sim q}[f(x) \frac{p(x)}{q(x)}] = E_{x \sim q}[(f(x) \frac{p(x)}{q(x)}) ^ 2] - (E_{x \sim q}[(f(x) \frac{p(x)}{q(x)})]) ^ 2 = E_{x \sim p}[f(x) ^ 2 \frac{p(x)}{q(x)}] - (E_{x \sim p}[f(x)]) ^ 2 Dx∼q[f(x)q(x)p(x)]=Ex∼q[(f(x)q(x)p(x))2]−(Ex∼q[(f(x)q(x)p(x))])2=Ex∼p[f(x)2q(x)p(x)]−(Ex∼p[f(x)])2
举例说明当 p p p 和 q q q 差距比较大时可能发生的问题:

将重要性采样应用到 off-policy 情形,就可以把 on-policy 算法改进成 off-policy 算法。
具体地,根据策略梯度法的梯度更新公式:
on-policy:
▽ R ˉ θ = E τ ∼ p θ ( τ ) [ R ( τ ) ▽ ln p θ ( τ ) ] \triangledown \bar R_{\theta} = E_{\tau \sim p_{\theta}(\tau)}[R(\tau) \triangledown \ln p_{\theta}(\tau)] ▽Rˉθ=Eτ∼pθ(τ)[R(τ)▽lnpθ(τ)]
off-policy:
▽ R ˉ θ = E τ ∼ p θ ′ ( τ ) [ p θ ( τ ) p θ ′ ( τ ) R ( τ ) ▽ ln p θ ( τ ) ] \triangledown \bar R_{\theta} = E_{\tau \sim p_{\theta^\prime}(\tau)}[\frac{p_{\theta}(\tau)}{p_{\theta^\prime}(\tau)} R(\tau) \triangledown \ln p_{\theta}(\tau)] ▽Rˉθ=Eτ∼pθ′(τ)[pθ′(τ)pθ(τ)R(τ)▽lnpθ(τ)]
实际在更新梯度时,是对每个“状态-动作”分开计算,即:
on-policy:
▽ R ˉ θ = E ( s t , a t ) ∼ π θ [ A θ ( s t , a t ) ▽ ln p θ ( a t n ∣ s t n ) ] \triangledown \bar R_{\theta} = E_{(s_t, a_t) \sim \pi_\theta}[A^{\theta}(s_t, a_t) \triangledown \ln p_{\theta}(a^n_t | s^n_t)] ▽Rˉθ=E(st,at)∼πθ[Aθ(st,at)▽lnpθ(atn∣stn)]
off-policy:
▽ R ˉ θ = E ( s t , a t ) ∼ π θ ′ [ p θ ( s t , a t ) p θ ′ ( s t , a t ) A θ ′ ( s t , a t ) ▽ ln p θ ( a t n ∣ s t n ) ] \triangledown \bar R_{\theta} = E_{(s_t, a_t) \sim \pi_{\theta^\prime}}[\frac{p_\theta(s_t, a_t)}{p_{\theta^\prime}(s_t, a_t)} A^{\theta^\prime}(s_t, a_t) \triangledown \ln p_{\theta}(a^n_t | s^n_t)] ▽Rˉθ=E(st,at)∼πθ′[pθ′(st,at)pθ(st,at)Aθ′(st,at)▽lnpθ(atn∣stn)]
由于:
p θ ( s t , a t ) = p θ ( a t ∣ s t ) p θ ( s t ) p θ ′ ( s t , a t ) = p θ ′ ( a t ∣ s t ) p θ ′ ( s t ) p_\theta(s_t, a_t) = p_\theta(a_t | s_t) p_\theta(s_t) \\ p_{\theta^\prime}(s_t, a_t) = p_{\theta^\prime}(a_t | s_t) p_{\theta^\prime}(s_t) pθ(st,at)=pθ(at∣st)pθ(st)pθ′(st,at)=pθ′(at∣st)pθ′(st)
于是得到下式:
E ( s t , a t ) ∼ π θ ′ [ p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) p θ ( s t ) p θ ′ ( s t ) A θ ′ ( s t , a t ) ▽ ln p θ ( a t n ∣ s t n ) ] E_{(s_t, a_t) \sim \pi_{\theta^\prime}}[\frac{p_\theta(a_t | s_t)}{p_{\theta^\prime}(a_t | s_t)} \frac{p_\theta(s_t)}{p_{\theta^\prime}(s_t)} A^{\theta^\prime}(s_t, a_t) \triangledown \ln p_{\theta}(a^n_t | s^n_t)] E(st,at)∼πθ′[pθ′(at∣st)pθ(at∣st)pθ′(st)pθ(st)Aθ′(st,at)▽lnpθ(atn∣stn)]
由于 actor 会看到的状态与其采取的动作关系不大,而且 p θ ( s t ) p_\theta(s_t) pθ(st) 很难算,因此假设 p θ ( s t ) = p θ ′ ( s t ) p_\theta(s_t) = p_{\theta^\prime}(s_t) pθ(st)=pθ′(st),将 p θ ( s t ) p θ ′ ( s t ) \frac{p_\theta(s_t)}{p_{\theta^\prime}(s_t)} pθ′(st)pθ(st) 删掉,得:
E ( s t , a t ) ∼ π θ ′ [ p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) A θ ′ ( s t , a t ) ▽ ln p θ ( a t n ∣ s t n ) ] ∗ E_{(s_t, a_t) \sim \pi_{\theta^\prime}}[\frac{p_\theta(a_t | s_t)}{p_{\theta^\prime}(a_t | s_t)} A^{\theta^\prime}(s_t, a_t) \triangledown \ln p_{\theta}(a^n_t | s^n_t)] \quad * E(st,at)∼πθ′[pθ′(at∣st)pθ(at∣st)Aθ′(st,at)▽lnpθ(atn∣stn)]∗
上式为梯度公式,可以通过梯度反推原目标函数,由:
▽ f ( x ) = f ( x ) ▽ ln f ( x ) \triangledown f(x) = f(x) \triangledown \ln f(x) ▽f(x)=f(x)▽lnf(x)
可得目标函数:
J θ ′ ( θ ) = E ( s t , a t ) ∼ π θ ′ [ p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) A θ ′ ( s t , a t ) ] J^{\theta^\prime}(\theta) = E_{(s_t, a_t) \sim \pi_{\theta^\prime}}[\frac{p_\theta(a_t | s_t)}{p_{\theta^\prime}(a_t | s_t)} A^{\theta^\prime}(s_t, a_t)] Jθ′(θ)=E(st,at)∼πθ′[pθ′(at∣st)pθ(at∣st)Aθ′(st,at)]
写成 J θ ′ ( θ ) J^{\theta^\prime}(\theta) Jθ′(θ) 是因为,括号里的 θ \theta θ 代表要去优化的参数, θ ′ \theta^\prime θ′ 是真正在与环境互动用作示范的参数。 J θ ′ ( θ ) J^{\theta^\prime}(\theta) Jθ′(θ) 是可以计算的,而更新参数则按照 ∗ * ∗ 式进行。
在前面介绍重要性采样时提到,如果 p θ ( a t ∣ s t ) p_\theta(a_t | s_t) pθ(at∣st) 和 p θ ′ ( a t ∣ s t ) p_{\theta^\prime}(a_t | s_t) pθ′(at∣st) 相差很多,采样结果就会不好。因此,避免两者相差太多就是 PPO 算法要做的事情。
在 PPO 算法中,除本来要优化的目标之外,又加入了一项约束:
J P P O θ ′ ( θ ) = J θ ′ ( θ ) − β K L ( θ , θ ′ ) J^{\theta^\prime}_{PPO}(\theta) = J^{\theta^\prime}(\theta) - \beta KL(\theta, \theta^\prime) JPPOθ′(θ)=Jθ′(θ)−βKL(θ,θ′)
其中, K L ( θ , θ ′ ) KL(\theta, \theta^\prime) KL(θ,θ′) 表示 KL 散度,用于度量 θ \theta θ 与 θ ′ \theta^\prime θ′ 之间的差异; β \beta β 大于 0 0 0,用于调节约束程度。
需要注意的是,这里讲的 θ \theta θ 与 θ ′ \theta^\prime θ′ 之间的差异(或者说距离),并非参数上的差异,而是行为(behaviour)上的差异;此外,并不一定要用 KL 散度来度量,L1 和 L2 范数也可以。
有关 KL 散度:

KL 散度也叫相对熵,恒非负,其值越大, P P P 与 Q Q Q 的差异越大,当 P ≡ Q P \equiv Q P≡Q 时取 0 0 0。
PPO 算法有一个前身,即 信任区域策略优化(TRPO,trust region policy optimization) ,采用直接约束 KL 散度的方式:
J T R P O θ ′ ( θ ) = J θ ′ ( θ ) K L ( θ , θ ′ ) < δ J^{\theta^\prime}_{TRPO}(\theta) = J^{\theta^\prime}(\theta) \quad \quad KL(\theta, \theta^\prime) < \delta JTRPOθ′(θ)=Jθ′(θ)KL(θ,θ′)<δ
但由于基于梯度进行优化时,约束很难处理,因此通常采用 PPO,而非 TRPO。
此外,PPO 与 TRPO 的性能相近,但是 PPO 的算法实现容易得多。
上述 PPO 算法为 PPO1 算法 ,通过使用 KL 散度进行惩罚(penalty)的方式,保证 θ \theta θ 与 θ ′ \theta^\prime θ′ 之间的相似性,因此也叫近端策略优化惩罚(PPO-penalty)。
关于 PPO1,还有一个 自适应 KL 散度(adaptive KL divergence) 的方法,即对参数 β \beta β 进行动态调整:
当 K L ( θ , θ ′ ) > K L max KL(\theta, \theta^\prime) > KL_{\max} KL(θ,θ′)>KLmax 时,说明惩罚项没有发挥作用,调大 β \beta β;
当 K L ( θ , θ ′ ) < K L min KL(\theta, \theta^\prime) < KL_{\min} KL(θ,θ′)<KLmin 时,说明惩罚项的效果过强,调小 β \beta β。
除 PPO1 外,还有一个 PPO2 算法 ,不需要计算 KL 散度,而是通过裁剪(clip)的方式进行约束,即近端策略优化裁剪(PPO-clip):
J P P O 2 θ ′ ( θ ) ≈ ∑ ( s t , a t ) min ( p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) A θ ′ ( s t , a t ) , c l i p ( p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) , 1 − ϵ , 1 + ϵ ) A θ ′ ( s t , a t ) ) J^{\theta^\prime}_{PPO2}(\theta) \approx \sum_{(s_t, a_t)} \min(\frac{p_\theta(a_t | s_t)}{p_{\theta^\prime}(a_t | s_t)} A^{\theta^\prime}(s_t, a_t), \quad clip(\frac{p_\theta(a_t | s_t)}{p_{\theta^\prime}(a_t | s_t)}, 1 - \epsilon, 1 + \epsilon) \ A^{\theta^\prime}(s_t, a_t)) JPPO2θ′(θ)≈(st,at)∑min(pθ′(at∣st)pθ(at∣st)Aθ′(st,at),clip(pθ′(at∣st)pθ(at∣st),1−ϵ,1+ϵ) Aθ′(st,at))
裁剪的原理如下:
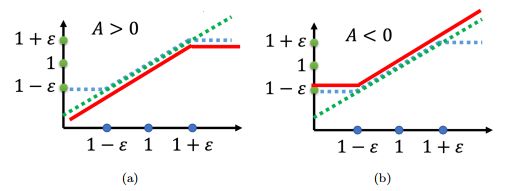
当优势函数 A > 0 A > 0 A>0 时, 我们希望 p θ ( a t ∣ s t ) p_\theta(a_t | s_t) pθ(at∣st) 越大越好,但是大于 1 + ϵ 1 + \epsilon 1+ϵ 就没有好处了;
当优势函数 A < 0 A < 0 A<0 时,我们希望把 p θ ( a t ∣ s t ) p_\theta(a_t | s_t) pθ(at∣st) 减小,但是减到 1 − ϵ 1 - \epsilon 1−ϵ 就可以了,不要压得更小。
总之,就是不要让 p θ ( a t ∣ s t ) p_\theta(a_t | s_t) pθ(at∣st) 和 p θ ′ ( a t ∣ s t ) p_{\theta^\prime}(a_t | s_t) pθ′(at∣st) 的差距太大。