actor-critic 相关算法简述

本文通过整理李宏毅老师的机器学习教程的内容，简要介绍深度强化学习（deep reinforcement learning）中基于 actor-critic 的相关算法。

李宏毅老师课程的B站链接：
李宏毅, 深度强化学习, actor-critic

相关笔记：
策略梯度法（policy gradient）算法简述
近端策略优化（proximal policy optimization）算法简述
DQN（deep Q-network）算法简述

asynchronous advantage actor-critic（A3C）

参考文献：
Volodymtr Mnih, Adria Puigdomenech Badia, Mehdi Mirza, Alex Graves, Timothy P. Lillicrap, Tim Harley, David Silver, Koray Kavukcuoglu, “Asynchronous Methods for Deep Reinforcement Learning”, ICML 2016

在基于 actor-critic 的相关算法里面，最知名的方法是 asynchronous advantage actor-critic，简称 A3C。
如果去掉异步（asynchronous），就是 advantage actor-critic，即 A2C。

首先回顾一下策略梯度法：
$$▽{\bar{R}}_{\theta }\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}(\sum _{t^{\prime }=t}^{T_n}{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}^n-b)▽\ln p_{\theta }(a_t^n|s_t^n)$$

记累计激励为 $G$：
$$G_t^n=\sum _{t^{\prime }=t}^{T_n}{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}^n$$

但是由于互动的过程本身是有随机性的，累计激励可能很不稳定，而每次更新参数前的采样次数又不可能很多，就有可能出现问题：

于是考虑用累计激励 $G$ 的期望值来代替采样的值，获取期望的方法就是基于价值的（value-based）方法，即 DQN。

DQN 有两种 critic，即状态价值函数（state value function）$V^{\pi }(s)$ 和状态-动作价值函数（state-action value function）$Q^{\pi }(s,a)$：

其中，使用基于蒙特卡洛的方法（Monte-Carlo based approach, MC）和基于时序差分的方法（temporal-difference approach, TD）的估计方法均可，时序差分比较稳定，蒙特卡罗比较精确。

实际上，累计激励 $G$ 的期望值就是 $Q$，即：
$$E[G_t^n]=Q^{{\pi }_{\theta }}(s_t^n,a_t^n)$$

关于基线，一个常见的做法使用状态价值函数 $V^{{\pi }_{\theta }}(s_t^n)$ 来表示，即：

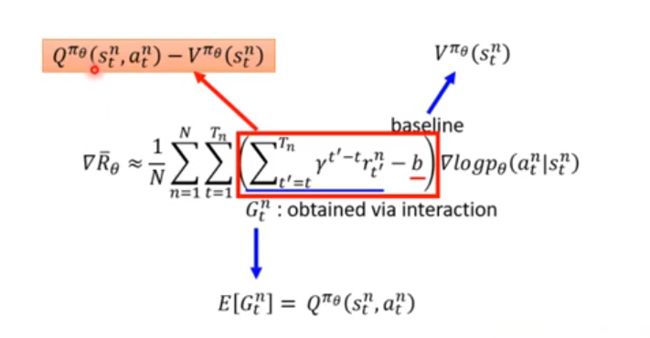
上述方法的缺点是，需要估计 $Q$ 和 $V$ 两个网络，估计不准确的风险会加倍。实际上，我们可以只估计一个网络，即 $V$ 网络，用 $V$ 的值来表示 $Q$ 的值。由于：
$$Q^{\pi }(s_t^n,a_t^n)=E[r_t^n+V^{\pi }(s_{t+1}^n)]$$

把期望去掉，即可直接用 $V$ 表示 $Q$：
$$Q^{\pi }(s_t^n,a_t^n)=r_t^n+V^{\pi }(s_{t+1}^n)$$

于是得到优势函数（advantage）的表达式：
$$r_t^n+V^{\pi }(s_{t+1}^n)-V^{\pi }(s_t^n)$$

更新策略 $\pi$ 的策略梯度公式即为：
$$▽{\bar{R}}_{\theta }\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}(r_t^n+V^{\pi }(s_{t+1}^n)-V^{\pi }(s_t^n))▽\ln p_{\theta }(a_t^n|s_t^n)$$

至于去掉期望值的原因，是原始 A3C 论文尝试各种方法进行实验比较的结果。

整体流程如下：

在策略梯度方法中，收集资料后，就要拿去更新策略；
但是在 actor-critic 方法中，不是直接用那些资料去更新策略，而是先用这些资料去估计价值函数 $V$ （可以用基于蒙特卡罗的方法或基于时序差分的方法），再基于价值函数，使用上式更新策略 $\pi$。

这里有两个技巧。

其一，在实现 actor-critic 时，我们需要估计两个网络，即 $V$ 函数的网络和策略的网络 $\pi$。由于这两个网络的输入都是状态 $s$，因此前面几层是可以共享的，尤其是输入为图像的游戏：

其二，我们需要探索（exploration）的机制。一个常见的方法是对策略 $\pi$ 的输出做一个约束，使输出分布的熵（entropy）不要太小，即希望不同的动作被探索的概率平均一些。这样可以尝试各种不同的动作，对环境探索得更好。

上述算法即为 advantage actor-critic（A2C），最后解释什么是异步（asynchronous）。

如下图所示，每个 actor 都是并行运行的，即“各做各的，不管彼此”，当某个进程运行结束准备回传参数时，原来的参数可能已经被其他 actor 覆盖了，但也没关系，直接更新就可以了，即为“异步”。
（注：图中的 $△\theta$ 应为 $▽\theta$）

pathwise derivative policy gradient

参考文献：
David Silver, Guy Lever, Nicolas Heess, Thomas Degris, Daan Wierstra, Martin Riedmiller, “Deterministic Policy Gradient Algorithms”, ICML 2014
Timothy P. Lillicrap, Jonathan J. Hunt, Alexander Pritzel, Nocolas Heess, Tom Erez, Yuval Tassa, David Silver, Daan Wierstra, “Continuous Control with Deep Reinforcement Learning”, ICLR 2016

接下来介绍 pathwise derivative policy gradient 算法。该算法的思路是，critic 不止评价动作的好坏，还要告诉 actor 什么动作是好的，即：
$$\arg \underset{a}{\max }{Q}^{\pi }(s,a)$$

但是如果是连续动作的场景，求解上述优化问题会比较困难，所以可以另外学习一个网络来求解这个优化问题（类比 GAN）：

算法流程是，先用一个策略 $\pi$ 与环境互动，估计出 $Q$ 函数，然后固定 $Q$，再去学习策略 $\pi$，得到一个更好的 actor，如此循环往复，如下图所示：

类似目标网络（target network）中的真正 $Q$ 网络和目标 $Q$ 网络（参见 DQN 部分），该算法中也有两个 actor，即真正的 $\pi$ 和目标 $\hat{\pi }$。
此外，之前提到的技巧，如 replay buffer 和 exploration 等都能用到。

具体的流程如下（对比原始的 DQN）：

actor-critic 与 GAN 的关系

actor-critic 与 GAN 是很类似的，具体可参考论文：
David Pfau, Oriol Vinyals, “Connecting Generative Adversarial Networks and Actor-Critic Methods”, arXiv preprint 2016

两者都以很难训练闻名，所以文章中收集了各种方法，讲述了如何把 GAN 训练起来。又由于做 GAN 和 actor-critic 的是两群人，因此文章有列出两种算法中分别有哪些方法有人尝试过，如下图所示：