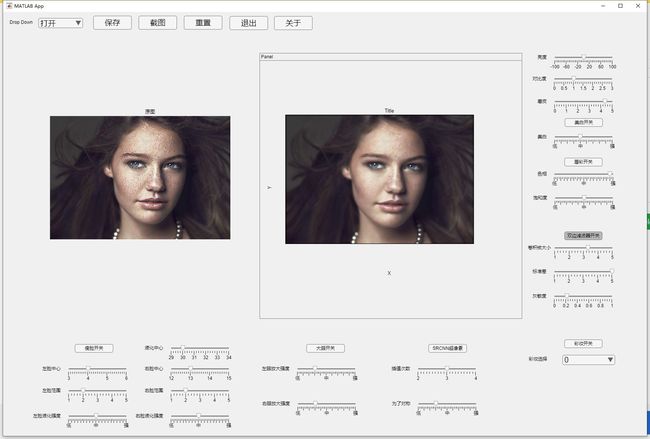
数字图像处理期末大作业-美图秀秀
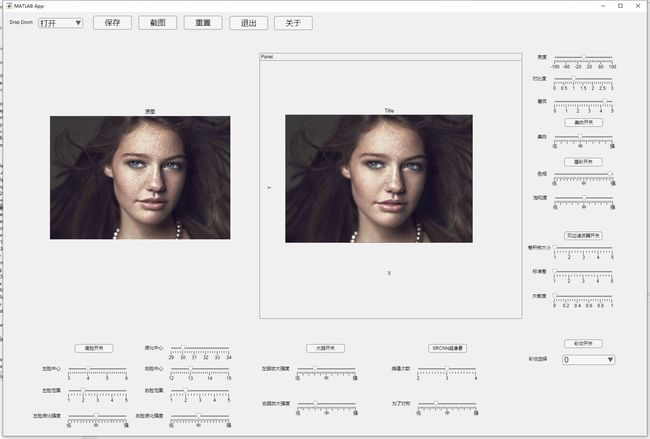
本项目是以matlab为主语言并设计GUI界面的一款简易美图秀秀,包含基础的图像处理和一些常见美颜算法
对于一些matlab较难实现的算法采用C++或python来实现
⭐️ github地址:https://github.com/mibbp/MeituShow
里面有我完整的代码,你想直接运行记得看readme配置一下环境,本博客更多的是讲解原理
《数字图像处理》
期末大作业
| 项目名称: | 简易版美图秀秀 |
|---|---|
| 班 级: | 数字媒体技术一班 |
| 姓 名: | 刘龙浩 |
| 学 号: | 20203317773154 |
西南石油大学信息学院
2022年10月24日
一、任务描述
近几年来随着各类直播场合、美颜相机 app 的不断出现,美化相片已经成为人们消遣的一种娱乐享受,尤其是在人们对美颜滤镜的需求也越来越多的情况下,这对广大年轻的朋友已成为不可或缺的需求。
美颜本质上是图像信号处理技术对于静态图像的应用,此次选择以美图秀秀作为期末课题,一方面是该课题会涉及到很多算法于数据结构,另一方面是相较其他课题更具挑战性
本项目主线实现功能点有:
-
简单的图像处理如增加图像亮度,对比度等
-
采用AWB算法美白人像
-
采用双边滤波算法磨皮
-
采用液化算法并用dlib提取特征点实现瘦脸
-
基于液化算法并用dlib提取特征点实现大眼
-
采用dlib提取特征点,采用Andrew求凸包并用BFS实现唇彩
-
采用SRCNN超分辨率算法实现提升照片像素
-
采用Beauty-GAN算法实现彩妆迁移
-
视频实时处理
-
交互式瘦脸
现今,与美颜相关的图像变形技术大量运用于动画和影视制作、短视频和直播、医学整形、身份代理、后代相貌预测等,未来,将有更广泛更广阔的应用。
二、设计思路
首先就是大体框架,我这里是先抽象设计,在我看来美图秀秀每个功能都是以下三步
- 获取照片
- 处理照片
- 输出照片
那就对这三步做分别处理就行,因为美图秀秀设计功能点相当多,为了避免冲突或逻辑出错所以前期框架要足够抽象能够适用所有情况,所以采用这三步为框架模型
获取照片
先是获取照片,获取照片途径有很多比如从文件夹选择、拍照、视频实时处理等等,但总的来说都是从某个流中获取一张照片罢了,即使是视频也可以把他拆分为多个连续的单一照片,为了所有功能都能适用于不同的图像以及图像流,所以最终处理的都是同一个图像变量,区别只是选择的输入流不同罢了,并且因为这个设计,导致我后续调用别的外部程序甚至多种语言的程序来处理都没有任何问题,初步只设计了文件夹选择照片和视频,后续要加其他获取照片途径可以直接添加,说简单点就是这么设计前面在花哨也不影响因为最终都会百川纳海
处理照片
首先,我的逻辑是要处理的都是同一个图像变量,美图秀秀涉及的功能点非常多,如果进行多个处理比如说先瘦脸在美白和先美白再瘦脸其实效果不一样甚至有些时候会出错,出现这个问题的原因就是处理的并不是同一个图像变量,因为顺序变了,所以要规定好一个处理顺序,保证所有的处理都是同一个照片不会出现因为顺序颠倒而产生逻辑问题
其次,大部分图像处理因为追求效果而导致实现复杂,所以效率不是更快,这里其实可以采用一些多线程并行处理或者使用GPU加速等一些技巧来提升效率,不过为了不要进行没必要的处理并且为了方便调试所以给每个处理都加了一个开关只有当开关打开才会执行该处理
输出照片
输出照片没啥好说的,最终都是把处理完的照片显示在该显示的区域罢了,区别就是最终输出的格式,比如照片有jpg、png,视频又有mp4、avi等格式但都不影响
三、功能模块
磨皮算法
先说最简单的磨皮算法,磨皮其实就是把人脸上不光滑的东西磨掉,那这些不光滑的东西其实就是噪点,所以可以很自然的想到运用一些滤波算法去做磨皮处理
均值滤波
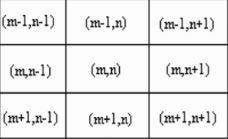
均值滤波无疑是最简单的,他的想法就是通过领域加权来达到滤波的目的,领域通常是指以自己为中心的周围八个元素,其实也就是一个 3 × 3 3 \times 3 3×3的卷积核或者说滤波器,八领域如下图所示
因为正常情况下都是照片上有噪点,也就是噪点数量远小于有效像素数量,而不是噪点上有照片,所以一个像素点周围八个元素一定是有效像素更多,那计算周围八个连带自己的总和除以9产生的新值就可以作为滤波后的像素值,因为有效像素比噪点多所以计算的均值一定是有效像素占比更大,然后遍历每个像素点都对他求一个八邻域均值,整体过程其实就是个卷积
高斯滤波
均值滤波的加权其实就是大家都是1,所以算下来的结果就是平均值,看上去很公平,但是实际上并不是,对于离目标像素点理应权重更大(明明是我先来的),因为在一个低频区域(也就是联通区域)离得越近那我们应该更相似,那么距离我越近提供的有效信息也就越多,所以他的权重也应该更大,离的越远权重应该越低,而这很明显符合高斯函数的特征,而且人们认为大多数图片噪声是符合高斯分布的(就是正态分布,由中心极限定理表明,一个随机变量如果是由大量微小的、独立的随机因素的叠加结果,那么这个变量一般都可以认为服从正态分布),所以我们把滤波器的值改一下,改成基于距离的高斯函数加权
高斯函数(正态分布函数)如下所示
G ( x , y ) = 1 2 π σ 2 e − x 2 + y 2 2 σ 2 G(x,y) = \frac {1}{2\pi\sigma^2}e^{- \frac{x^2+y^2}{2\sigma^2}} G(x,y)=2πσ21e−2σ2x2+y2
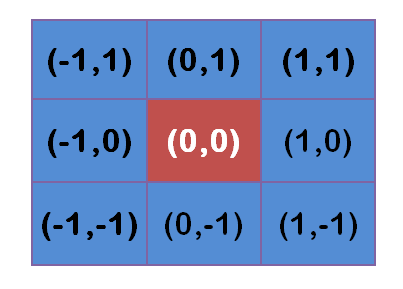
假设中心点坐标为 ( 0 , 0 ) (0,0) (0,0),那么他的八邻域就分别为
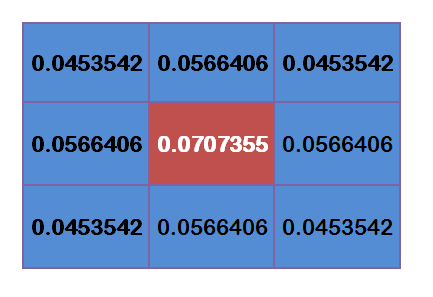
然后计算出距离套高斯函数,这里设 σ = 1.5 \sigma = 1.5 σ=1.5,则模糊半径为1的权重矩阵为
但是还得进行归一化,也就是让他们的权重之和为1,因为得保证他们和其他处理处于同一量级,对于上面的值分别处以0.4787147就好了
但你实际写代码很简单matlab这些都有自带实现好的,可以看看高斯滤波的效果
运行结果
磨皮效果还凑合
双边滤波
虽然高斯滤波效果还凑合但是他有个致命问题那就是他会模糊五官,这是我们不想看到的,为了不模糊五官我们可以采用保边滤波算法,其中双边滤波就是最经典简单的保边滤波了
先说为什么高斯滤波会模糊五官,因为它只关注位置信息,高斯滤波认为距离中心点越近权重越大,这种只关注距离的思想在某些情况是可行的,比如在低频平坦区域,距离越近的像素肯定分布越相近,但是在高频边缘区域,这种方法就会适得其反,会损失掉有用的边缘信息,这个时候就要用到保边滤波算法
想深入了解双边滤波算法原理的我建议看这两篇论文,我这里只做通俗的讲解
-
Fast O(1) Bilateral Filtering Using Trigonometric Range Kernels
-
Fast Adaptive Bilateral Filtering
算法原理
我们可以很容易发现五官的边界和皮肤有很明显的区别(不然你可以看不出这个人有鼻子有眼的),也就是说在五官和皮肤的交界处一定会有极大的像素值差,原本的高斯滤波是只以距离差为变量,那我们在此基础上再加个像素值差,也就是说距离中心点距离越近权重越高,但是和中心点的像素值差值越大权重越小,且像素值差值的影响要大于距离值
于是就设计出双边滤波的一个公式
g ( p ) = η ( p ) − 1 ∑ q ∈ Ω G σ s ( ∥ p − q ∥ ) G σ r ( ∣ F ( p ) − F ( q ) ∣ ) F ( q ) η ( p ) = ∑ q ∈ Ω G σ s ( ∥ p − q ∥ ) G σ r ( ∣ F ( p ) − F ( q ) ∣ ) G σ s ( ∥ p − q ∥ ) = e − ( i − m ) 2 + ( j − n ) 2 2 σ s 2 G σ r ( ∣ F ( p ) − F ( q ) ∣ ) = e − [ F ( i , j ) − F ( m , n ) ] 2 2 σ r 2 p , q 表 示 像 素 点 , F ( p ) 表 示 该 点 像 素 值 Ω 表 示 图 片 , ( i , j ) 为 卷 积 核 中 心 ( m , n ) 则 表 示 卷 积 核 中 心 周 围 其 他 值 g(p) = \eta(p)^{-1}\sum_{q\in\Omega}G_{\sigma_s}(\Vert p-q\Vert) G_{\sigma_r}(\vert F(p)-F(q)\vert)F(q) \\ \eta(p) = \sum_{q\in\Omega}G_{\sigma_s}(\Vert p-q\Vert) G_{\sigma_r}(\vert F(p)-F(q)\vert) \\ G_{\sigma_s}(\Vert p-q\Vert) = e^{-\frac {(i-m)^2+(j-n)^2} {2\sigma_s^2} } \\ G_{\sigma_r}(\vert F(p)-F(q)\vert) = e^{-\frac {[F(i,j)-F(m,n)]^2} {2\sigma_r2} } \\ p,q表示像素点,F(p)表示该点像素值 \\ \Omega 表示图片,(i,j)为卷积核中心 \\ (m,n)则表示卷积核中心周围其他值 g(p)=η(p)−1q∈Ω∑Gσs(∥p−q∥)Gσr(∣F(p)−F(q)∣)F(q)η(p)=q∈Ω∑Gσs(∥p−q∥)Gσr(∣F(p)−F(q)∣)Gσs(∥p−q∥)=e−2σs2(i−m)2+(j−n)2Gσr(∣F(p)−F(q)∣)=e−2σr2[F(i,j)−F(m,n)]2p,q表示像素点,F(p)表示该点像素值Ω表示图片,(i,j)为卷积核中心(m,n)则表示卷积核中心周围其他值
这个公式看着很吓人其实真的很简单,但其实就是俩高斯函数的叠加一个是以距离为变量一个是以像素差值为变量,并做卷积求和, η ( p ) − 1 \eta(p)^{-1} η(p)−1是用来做归一化处理的, G σ s ( ∥ p − q ∥ ) G_{\sigma_s}(\Vert p-q\Vert) Gσs(∥p−q∥) 就是以像素值为变量的高斯函数, G σ r ( ∣ F ( p ) − F ( q ) ∣ ) G_{\sigma_r}(\vert F(p)-F(q)\vert) Gσr(∣F(p)−F(q)∣) 则是以像素差值为变量的高斯函数,具体分析可以看论文或者私聊问我
代码
% 双边滤波器
function results = B_filter(~,Img,tempsize,sigma0,sigma1)
gauss = fspecial('gauss',2*tempsize+1,sigma0);
[m,n] = size(Img);
% tempsize为卷积核大小
for i = 1+ tempsize : m - tempsize
for j = 1+ tempsize : n - tempsize
% 提取处理区域得到梯度敏感矩阵
% 得到灰度差值矩阵,并用高斯函数处理为灰度差越大则最终数值越小的权重矩阵
temp = abs(Img(i - tempsize:i + tempsize,j - tempsize:j + tempsize) - Img(i,j));
temp = exp(-temp.^2/(2*sigma1^2));
%将权重矩阵与高斯滤波器相乘,得到双边滤波器,并将权值和化为一
filter = gauss.*temp;
filter = filter/sum(filter(:));
% 卷积求和
Img(i,j) = sum(sum((Img(i - tempsize:i + tempsize,j - tempsize:j + tempsize).*filter)));
end
end
results = Img;
end
% 双边滤波函数
function results = BF(app,I)
tempsize = round(app.Slider_4.Value); %控制卷积核大小的参数
sigma1 = round(app.Slider_5.Value); %控制标准差
sigma2 = app.Slider_6.Value; %控制灰度的敏感性,越大的灰度差,权重越小
%模板补零,便于卷积操作,不然会使得图片区域出现黑边
img = double(padarray(I,[tempsize,tempsize],0))/255;
imgr = img(:,:,1);
imgg = img(:,:,2);
imgb = img(:,:,3);
img(:,:,1) = app.B_filter(imgr,tempsize,sigma1,sigma2);
img(:,:,2) = app.B_filter(imgg,tempsize,sigma1,sigma2);
img(:,:,3) = app.B_filter(imgb,tempsize,sigma1,sigma2);
results = img;
end
效果对比
瘦脸算法
这一块我是用python写的主要是matlab没有找到比较好的提取特征点的模型,如果提取特征点不精确很多算法效果都不会很好,所以改用python去写,C++也可以写效果比python好,但是matlab调用python要更简单一些,c++的生成mex文件才行还得按照他的规则来写
瘦脸算法本质上就是人脸图像变形算法,人脸图像变形技术主要有两个比较关键的,一个是空间映射,另一个就是重采样技术,空间映射又分为前向映射和后向映射,我们采用的使后向映射一般都是后向映射,因为后向映射变形后的图像能稳定、平滑地过渡变化,并得到良好的渐变效果,满足人的视觉感官体验。
人脸特征点
人脸特征主要应具有普遍性(人人拥有)、唯一性(人人不同)、稳定性(不因时间、年龄、环境的变化而变化)和采集方便性(应釆集容易、设备简单、对人影响程度小)等特点。比如人脸轮廓,五官那些
人脸检测
我们实际使用的训练好的模型提取特征点,但这里还是大概讲一下算法原理
想提取人脸特征首先的检测到人脸才行,检测人脸我应该在上课时候讲了一下,这里就懒得打字了,建议直接看论文
基于Harr特征
Harr-like特征是Viola等提出的一种简单矩形特征,因其类似于Harr小波而得名,脸部的一些特征可以由矩形特征简单的描绘,如下图示范:
上图中两个矩形特征,表示出人脸的某些特征。比如中间一幅表示眼睛区域的颜色比脸颊区域的颜色深,右边一幅表示鼻梁两侧比鼻梁的颜色要深
矩形特征对一些简单的图形结构,比如边缘、线段,比较敏感,但是其只能描述特定走向(水平、垂直、对角)的结构,因此比较粗略。如上图,脸部一些特征能够由矩形特征简单地描绘,例如,通常眼睛要比脸颊颜色更深;鼻梁两侧要比鼻梁颜色要深;嘴巴要比周围颜色更深。
对于一个 24×24 检测器,其内的矩形特征数量超过160,000个,必须通过特定算法甄选合适的矩形特征,并将其组合成强分类器才能检测人脸。
常用的矩形特征有三种:两矩形特征、三矩形特征、四矩形特征,如图:
特征值计算
特征矩阵的特征值就是白色区域像素值减去黑色区域像素值,因为矩阵数量很多,所以需要一个能够快速计算矩阵区间和的算法也就是二维前缀和算法,这玩意很简单网上一搜就会,就是求出 s u m ( x , y ) sum(x,y) sum(x,y), s u m ( x , y ) sum(x,y) sum(x,y)的意思就是以图形左上角 ( 0 , 0 ) (0,0) (0,0)为矩阵左上顶点, x , y x,y x,y为右下顶点,计算除该矩阵的像素和,只需 O ( N M ) O(NM) O(NM)的时间复杂度就可以预处理出来
然后查询的时间复杂度是 O ( 1 ) O(1) O(1)的,如下图所示我们相求X矩阵的像素值
因为绿色、紫色、红色、蓝色矩阵都已经求出来了所以直接绿色减去蓝色和紫色然后再加上重复相减的红色区域就是X矩阵的像素值
Adaboost训练人脸检测模型
刚刚说了我们需要得到一个好的特征矩阵来提取特征,但是我们不知道那个好,那我们就找到所有的特征矩阵然后训练找到那个比较好的
这个算法原理其实就是三个臭皮匠,顶个诸葛亮,我上课应该也做了演示,这里简单说一下流程就是先来一个弱分类器,可以很垃圾甚至你写给随机给值都行(就是这样工作量会变大所以一般都是会选个最优弱分类器),然后对他初始赋权都一样然后进行初步训练,训练后可能有些表现得很好有些不好,然后就调整权重,把那些效果不好的权重拉高然后降低好的生成第二个模型,然后再根据结果调整权重,最后把所有训练得结果分配权重整合起来就变成了强分类器
弱分类器的训练和选取
以20*20图像为例,78,460个特征,如果直接利用AdaBoost训练,那么工作量是极其极其巨大的。
所以必须有个筛选的过程,筛选出T个优秀的特征值(即最优弱分类器),然后把这个T个最优弱分类器传给AdaBoost进行训练。
现在有人脸样本2000张,非人脸样本4000张,这些样本都经过了归一化,大小都是20x20的图像。那么,对于78,460中的任一特征 f i f_i fi,我们计算该特征在这2000人脸样本、4000非人脸样本上的值,这样就得到6000个特征值。将这些特征值排序,然后选取一个最佳的特征值,在该特征值下,对于特征 f i f_i fi来说,样本的加权错误率最低。
弱分类器训练过程大致为以下几步
-
对每个特征,计算所有训练样本的特征值
-
将特征值排序
-
排完序后遍历对每个元素计算
- 全部正例权重和记为 T + T^+ T+
- 全部负例权重和记为 T − T^- T−
- 该元素前正例权重和记为 S + S^+ S+
- 该元素前负例权重和记为 S − S^- S−
-
选取当前元素的特征值 和它前面的一个特征值之间的数作为阈值,所得到的弱分类器就在当前元素处把样本分开 —— 也就是说这个阈值对应的弱分类器将当前元素前的所有元素分为人脸(或非人脸),而把当前元素后(含)的所有元素分为非人脸(或人脸)。该阈值的分类误差为:
e = m i n ( S + + ( T − − S − ) , S − + ( T + − S + ) ) e = min(S^+ + (T^--S^-),S^-+(T^+-S^+)) e=min(S++(T−−S−),S−+(T+−S+))
正列就是正样本,可以理解为正值,就我们会为每个点分配一个权重,分配正确的为正数,错误的是负数,比如人脸就是正样本,非人脸就是负样本
由于一共有78,460个特征、因此会得到78,460个最优弱分类器,在78,460个特征中,我们选取错误率最低的特征,用来判断人脸,同时用此分类器对样本进行分类,并更新样本的权重。
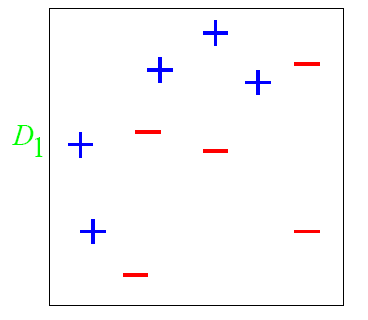
有一个非常经典的例子就是
图中’+‘和’-'表示不同的类别,我们想训练出一个特征矩阵能够分出这两类,一开始都赋一样的权比如0.1,第一次训练出的结果是这样的
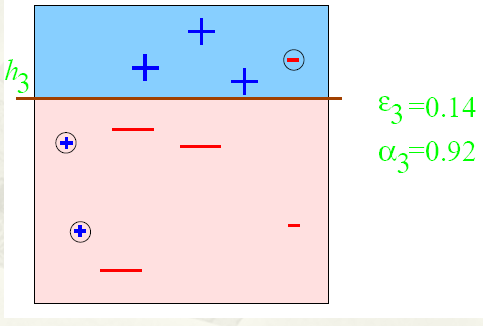
权重都是一样的话那这样就是最理想的,因为左边都是正列,右边加进来就会变差,但是这个还不行因为还有很多正列没有被包含进来,这时候我们把那些没被包含进来的正列加权,对已经加进来的正列减全,这样第二次训练就变成了
虽然把所有正列都包进来了但是还是有一些负的,所以把负的权重增大,包含进来的正的减小,这样第三次训练就变成了
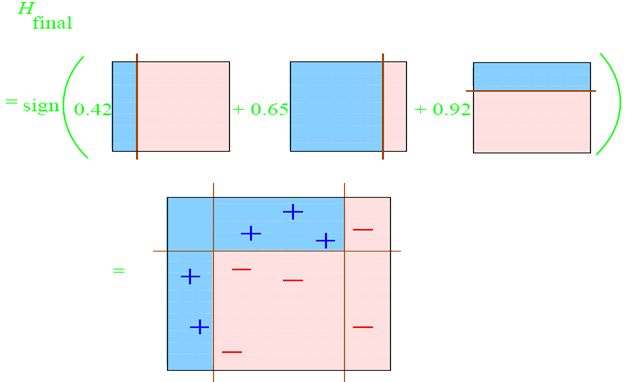
然后把这三次训练加权结合就变成了最终的强分类器
特征点提取
特征点提取也有很多算法,感兴趣的可以自行去了解吧,比如HOG,CNN这些
我这里采用的是dlib模型提取人脸68个特征点,因为我自己尝试了写之后发现效果很差不如直接用别人训练好的模型(我是fw)
配置好CMake dlib opencv等环境
"""
作者:Mibbp
日期: 2022年10月30日
"""
import dlib
import cv2
import numpy as np
import math
predictor_path = 'D:/dlib-shape/shape_predictor_68_face_landmarks.dat' # 导入模型
# 使用dlib自带的frontal_face_detector作为我们的特征提取器
detector = dlib.get_frontal_face_detector()
predictor = dlib.shape_predictor(predictor_path)
def landmark_dec_dlib_fun(img_src):
img_gray = cv2.cvtColor(img_src, cv2.COLOR_BGR2GRAY)
land_marks = []
rects = detector(img_gray, 0)
for i in range(len(rects)):
land_marks_node = np.matrix([[p.x, p.y] for p in predictor(img_gray, rects[i]).parts()])
for idx,point in enumerate(land_marks_node):
# 68点坐标
pos = (point[0,0],point[0,1])
# print(idx,pos)
# 利用cv2.circle给每个特征点画一个圈,共68个
cv2.circle(img_src, pos, 5, color=(0, 255, 0))
# 利用cv2.putText输出1-68
font = cv2.FONT_HERSHEY_SIMPLEX
cv2.putText(img_src, str(idx + 1), pos, font, 0.3, (0, 0, 255), 1, cv2.LINE_AA)
land_marks.append(land_marks_node)
return land_marks
def main():
src = cv2.imread('C:/Users/mibbp/Pictures/xfsy_0068.jpg')
# cv2.imshow('src', src)
landmark_dec_dlib_fun(src)
cv2.imshow("src", src)
cv2.waitKey(0)
if __name__ == '__main__':
main()
如上图所示,其中1 ~ 17为人脸轮廓,18 ~ 22为左眉毛,23 ~ 27为右眉毛,28 ~ 36为鼻子,37 ~ 42为左眼,43 ~ 48为右眼,49 ~ 60为外嘴唇轮廓,61 ~ 68为内嘴唇或牙齿轮廓
液化算法
瘦脸算法有很多,本质上都是像素迁移或者图像扭曲算法,比如基于最小二乘法的MLS,还有这里介绍的液化算法
想深入理解的可以看论文,我这里只做通俗解释
-
MLS: Image Deformation Using Moving Least Squares
-
液化:Interactive Image Warping
-
人脸图像变形技术
算法原理
这些像素迁移或者图像扭曲算法,其实都可以看作是把某一个像素移动到一个目标位置,比如瘦脸就是把脸外围的像素往里收缩,实际上就是计算出目标点的位置,然后把当前点替换成目标点的像素就行,但是直接替换肯定使不行的,因为计算出的目标点坐标是实数,但是实际上像素点坐标都是整数,而且为了能够使变化后的图形更平滑,所以要用一些重采样技术进行一些插值处理
前向映射和后向映射
空间映射是指建立原图像与目标图像之间各对应像素点的映射关系的函数,而其中又分为前向映射和后向映射说人话前向映射就是指通过原图像某个像素点算出目标图像对应像素点,后向映射就是通过目标图像像素点算出他是由原图像那个点转移过去的
图像变形中,各像素点之间的映射关系一般不是一一对应的,会产生“空洞”和“混叠”现象(源图像中的多点映射到目标图像中的一点)的前向映射方式并不能满足图像变形过程中的要求,为了解决这一问题,我们可以采用非均勾采样、相交检测等方法,但是这些方法会带来空间和时间上开销较大的不利影响。为了保证变形图像的唯一性(没有“空洞”和“混叠”现象)、完整性,我们采用后向映射的方法可以很好地解决时间和空间上的开销问题,它将目标图像中的每个像素点都映射到源图像中对应的某个位置,这些位置的灰度值利用重釆样技术得到。由于后向映射在实现方式上很方便,仅用源图像中的特征作为目标特征,用变形后的图像即目标图像中的特征作为源特征建立映射关系就可以完成。因此后向映射成为主流的映射方式。
最近邻域插值
这个名字听着可厉害其实就是对求出的点的坐标四舍五入一下就好了,也就是求得的实数点 ( x , y ) (x,y) (x,y)的像素值 R G B ( x , y ) RGB(x,y) RGB(x,y)由距离该店最近的像素点RGB值替代
R G B ( x , y ) = R G B ( r o u n d ( x ) , r o u n d ( y ) ) RGB(x,y) = RGB(round(x),round(y)) RGB(x,y)=RGB(round(x),round(y))
领域平均插值
邻域平均插值将实数点处的灰度值用它的邻域像素点的平均值来代替。设点处的个最近邻像素为, A , B , C , D A,B,C,D A,B,C,D。它们的灰度值分别为 g r a y ( A ) , g r a y ( B ) , g r a y ( C ) , g r a y ( D ) gray(A),gray(B),gray(C),gray(D) gray(A),gray(B),gray(C),gray(D)。则
R G B ( x , y ) = R G B ( A ) + R G B ( B ) + R G B ( C ) + R R G B ( D ) 4 RGB(x,y) = \frac {RGB(A)+RGB(B)+RGB(C)+RRGB(D)} {4} RGB(x,y)=4RGB(A)+RGB(B)+RGB(C)+RRGB(D)
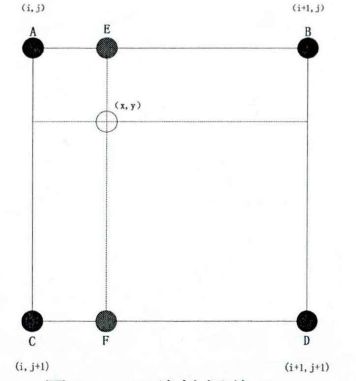
双线性插值
设 ( x , y ) (x,y) (x,y) 点处的 4 个最近邻像素 A , B , C , D A,B,C,D A,B,C,D 的坐标分别为 ( i , j ) , ( i , j + 1 ) , ( i + 1 , j ) , ( i + 1 , j + 1 ) (i,j),(i,j+1),(i+1,j),(i+1,j+1) (i,j),(i,j+1),(i+1,j),(i+1,j+1) 如图所示。
双线性插值按以下步骤计算处的灰度值:
首先计算 E , F E,F E,F 这两点的RGB值 R G B ( E ) , R G B ( F ) RGB(E),RGB(F) RGB(E),RGB(F):
R G B ( E ) = ( x − i ) [ R G B ( B ) − R G B ( A ) ] + R G B ( A ) R G B ( F ) = ( x − i ) [ R G B ( D ) − R G B ( C ) ] + R G B ( C ) RGB(E) = (x-i)[RGB(B)-RGB(A)]+RGB(A) \\ RGB(F) = (x-i)[RGB(D)-RGB(C)]+RGB(C) RGB(E)=(x−i)[RGB(B)−RGB(A)]+RGB(A)RGB(F)=(x−i)[RGB(D)−RGB(C)]+RGB(C)
则 ( x , y ) (x,y) (x,y)得RGB值为:
R G B ( x , y ) = ( y − j ) [ R G B ( F ) − R G B ( E ) ] + R G B ( E ) RGB(x,y) = (y-j)[RGB(F)-RGB(E)]+RGB(E) RGB(x,y)=(y−j)[RGB(F)−RGB(E)]+RGB(E)
相对于邻域平均插值和最近邻域插值,双线性插值虽然有较大的计算量,但其插值结果比较平滑。考虑到人脸图像需要高度的真实感,选择使用双线性插值进行重采样
液化算法思路
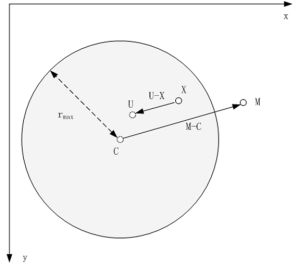
假设当前点为 X ( x , y ) X (x,y) X(x,y),指定变形区域的中心点为 C ( C x , C y ) C(C_x,C_y) C(Cx,Cy),变形区域半径为 r r r,调整变形终点(从中心点到某个位置M)为 M ( M x , M y ) M(M_x,M_y) M(Mx,My),变形程度为 s t r e n g t h strength strength,当前点对应变形后的目标位置为 U U U。变形规律如下,
-
圆内所有像素均沿着变形向量的方向发生偏移
-
距离圆心越近,变形程度越大
-
距离圆周越近,变形程度越小,当像素点位于圆周时,该像素不变形
-
圆外像素不发生偏移
U ⃗ = X ⃗ − ( r m a x 2 − ∣ X ⃗ − C ⃗ ∣ 2 ( r m a x 2 − ∣ X ⃗ − C ⃗ ∣ 2 ) + ∣ M ⃗ − C ⃗ ∣ 2 ) ( M ⃗ − C ⃗ ) \vec{U} = \vec{X} - \bigg(\frac{r_{max}^2 - \vert \vec{X}-\vec{C} \vert^2 }{(r_{max}^2 - \vert \vec{X}-\vec{C} \vert^2 ) + \vert \vec{M}-\vec{C} \vert^2}\bigg) (\vec{M}-\vec{C}) U=X−((rmax2−∣X−C∣2)+∣M−C∣2rmax2−∣X−C∣2)(M−C)
对上面公式进行改进,加入变形程度控制变量strength,改进后瘦脸公式如下
K 0 = 100 S t r e n g t h K 1 = ( x − C x ) 2 + ( y − C y ) 2 t x = ( r 2 − ( x − C x ) 2 ( r 2 − ( x − C x ) 2 ) + K 0 ( M x − C x ) 2 ) 2 ( M x − C x ) t y = ( r 2 − ( y − C y ) 2 ( r 2 − ( y − C y ) 2 ) + K 0 ( M y − C y ) 2 ) 2 ( M x − C x ) d x = x − t x ( 1.0 − K 1 r ) d y = y − t y ( 1.0 − K 1 r ) K_0 = \frac{100}{Strength} \\ K_1 = \sqrt(x-C_x)^2 + (y-C_y)^2 \\ t_x = \bigg( \frac{r^2-(x-C_x)^2}{(r^2-(x-C_x)^2) + K_0(M_x-C_x)^2} \bigg)^2 (M_x-C_x) \\ t_y = \bigg( \frac{r^2-(y-C_y)^2}{(r^2-(y-C_y)^2) + K_0(M_y-C_y)^2} \bigg)^2 (M_x-C_x) \\ d_x = x-t_x(1.0-\frac{K_1}{r}) \\ d_y = y-t_y(1.0-\frac{K1}{r}) K0=Strength100K1=(x−Cx)2+(y−Cy)2tx=((r2−(x−Cx)2)+K0(Mx−Cx)2r2−(x−Cx)2)2(Mx−Cx)ty=((r2−(y−Cy)2)+K0(My−Cy)2r2−(y−Cy)2)2(Mx−Cx)dx=x−tx(1.0−rK1)dy=y−ty(1.0−rK1)
代码
import dlib
import cv2
import numpy as np
import math
predictor_path = 'D:/dlib-shape/shape_predictor_68_face_landmarks.dat'
detector = dlib.get_frontal_face_detector()
predictor = dlib.shape_predictor(predictor_path)
def landmark_dec_dlib_fun(img_src):
img_gray = cv2.cvtColor(img_src, cv2.COLOR_BGR2GRAY)
land_marks = []
rects = detector(img_gray, 0)
for i in range(len(rects)):
land_marks_node = np.matrix([[p.x, p.y] for p in predictor(img_gray, rects[i]).parts()])
land_marks.append(land_marks_node)
return land_marks
def localTranslationWarp(srcImg, startX, startY, endX, endY, radius,Strength):
ddradius = float(radius * radius)
copyImg = np.zeros(srcImg.shape, np.uint8)
copyImg = srcImg.copy()
K0 = 100/Strength
ddmc = (endX - startX) * (endX - startX) + (endY - startY) * (endY - startY) # (m-c)^2
H, W, C = srcImg.shape
for i in range(W):
for j in range(H):
# 计算该点是否在形变圆的范围之内
# 优化,第一步,直接判断是会在(startX,startY)的矩阵框中
if math.fabs(i - startX) > radius and math.fabs(j - startY) > radius:
continue
distance = (i - startX) * (i - startX) + (j - startY) * (j - startY)
K1 = math.sqrt(distance)
if (distance < ddradius):
# 计算出(i,j)坐标的原坐标
# 计算公式中右边平方号里的部分
ratio = (ddradius - distance) / (ddradius - distance + K0 * ddmc)
ratio = ratio * ratio
# 映射原位置
UX = i - (ratio * (endX - startX) * (1.0 - (K1 / radius)))
UY = j - (ratio * (endY - startY) * (1.0 - (K1 / radius)))
# 根据双线性插值法得到UX,UY的值
value = BilinearInsert(srcImg, UX, UY)
# 改变当前 i ,j的值
copyImg[j, i] = value
return copyImg
# 双线性插值法
def BilinearInsert(src, ux, uy):
w, h, c = src.shape
if c == 3:
x1 = int(ux)
x2 = x1 + 1
y1 = int(uy)
y2 = y1 + 1
part1 = src[y1, x1].astype(np.float) * (float(x2) - ux) * (float(y2) - uy)
part2 = src[y1, x2].astype(np.float) * (ux - float(x1)) * (float(y2) - uy)
part3 = src[y2, x1].astype(np.float) * (float(x2) - ux) * (uy - float(y1))
part4 = src[y2, x2].astype(np.float) * (ux - float(x1)) * (uy - float(y1))
insertValue = part1 + part2 + part3 + part4
return insertValue.astype(np.int8)
def face_thin_auto(src,LStrength,RStrength,Lcen,Rcen,Lrad,Rrad,Center):
# src为原图像
# LStrength,RStrength为左右脸形变强度
# Lcen,Rcen为左右脸形变中心
# Lrad,Rrad为形变范围半径
# Center为形变重点一般就是人脸中心鼻子那一块
LStrength为
landmarks = landmark_dec_dlib_fun(src)
# print(landmarks)
# 如果未检测到人脸关键点,就不进行瘦脸
if len(landmarks) == 0:
return
for landmarks_node in landmarks:
# print(landmarks_node)
left_landmark = landmarks_node[Lcen]
left_landmark_down = landmarks_node[Lcen+Lrad]
right_landmark = landmarks_node[Rcen]
right_landmark_down = landmarks_node[Rcen+Rrad]
endPt = landmarks_node[Center]
# 计算第Lcen个点到第Lcen+Lrad个点的距离作为瘦脸距离
r_left = math.sqrt(
(left_landmark[0, 0] - left_landmark_down[0, 0]) * (left_landmark[0, 0] - left_landmark_down[0, 0]) +
(left_landmark[0, 1] - left_landmark_down[0, 1]) * (left_landmark[0, 1] - left_landmark_down[0, 1]))
# 计算第Rcen个点到第Rcen+Rrad个点的距离作为瘦脸距离
r_right = math.sqrt(
(right_landmark[0, 0] - right_landmark_down[0, 0]) * (right_landmark[0, 0] - right_landmark_down[0, 0]) +
(right_landmark[0, 1] - right_landmark_down[0, 1]) * (right_landmark[0, 1] - right_landmark_down[0, 1]))
# 瘦左边脸
thin_image = localTranslationWarp(src, left_landmark[0, 0], left_landmark[0, 1], endPt[0, 0], endPt[0, 1],
r_left,LStrength)
# 瘦右边脸
thin_image = localTranslationWarp(thin_image, right_landmark[0, 0], right_landmark[0, 1], endPt[0, 0],
endPt[0, 1], r_right,RStrength)
# 显示
# cv2.imshow('thin', thin_image)
# 保存
cv2.imwrite('C:/Users/mibbp/Pictures/thin.jpg', thin_image)
def test():
print("pytest1")
def main(LStrength,RStrength,Lcen,Rcen,Lrad,Rrad,Center):
LStrength = int(LStrength)
RStrength = int(RStrength)
Lcen = int(Lcen)
Rcen = int(Rcen)
Lrad = int(Lrad)
Rrad = int(Rrad)
Center = int(Center)
src = cv2.imread('C:/Users/mibbp/Pictures/pysltest.jpg')
# cv2.imshow('src', src)
face_thin_auto(src,LStrength,RStrength,Lcen,Rcen,Lrad,Rrad,Center)
cv2.waitKey(0)
if __name__ == '__main__':
main()
效果展示
大眼算法
这里和上一个瘦脸算法是一个东西其实,所以就不过多去讲原理了,就是逆变换了一下,就瘦脸我们说的是一个范围他往里收缩,越靠近中心收缩强度越大,越靠近边界越小,边界外不收缩,而大眼则是放过来,我们越靠近中心变化越小,越靠近边界变化越大,边界外不变,先说原版的我这里做了一点优化
原版
以眼睛中心为中心点,对眼睛区域向外放大,就实现了大眼的效果。大眼的基本公式如下
f s ( r ) = ( 1 − ( r r m a x − 1 ) 2 a ) r f_s(r) = \big(1-( \frac{r}{r_{max}} -1 )^2 a\big)r fs(r)=(1−(rmaxr−1)2a)r
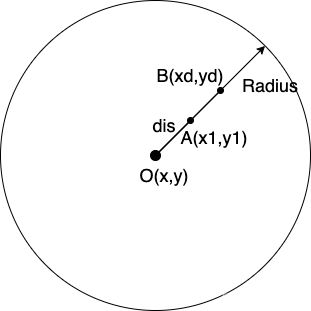
假设眼睛中心点为 O ( x , y ) O(x,y) O(x,y),大眼区域半径为 R a d i u s Radius Radius,当前点位为 A ( x 1 , y 1 ) A(x1,y1) A(x1,y1),对其进行改进,加入大眼程度形变强度变量Strength,其中Strength的取值范围为0~100。
d i s 2 = ( x 1 − x ) 2 + ( y 1 − y ) 2 K 0 = S t r e n g t h / 100.0 k = 1.0 − ( 1.0 − d i s 2 R a d i u s 2 ) K 0 x d = ( x 1 − x ) k + x y d = ( y 1 − y ) k + y dis^2 = (x_1-x)^2 + (y_1 - y)^2 \\ K_0 = Strength/100.0 \\ k = 1.0 - (1.0-\frac{dis^2}{Radius^2})K_0 \\ x_d = (x_1 - x)k+x y_d = (y_1 - y)k+y dis2=(x1−x)2+(y1−y)2K0=Strength/100.0k=1.0−(1.0−Radius2dis2)K0xd=(x1−x)k+xyd=(y1−y)k+y
Mbp-ImageWarping
原版的有一个最关键的问题就是眼睛是椭圆,你用圆形的效果并不是很好,你用圆形公式计算的中心半径啥的都不是准确的,所以这里我自己优化了一下,改成椭圆的了,中间肯定会涉及大量计算几何,如果我还是高三那我秒解,但是我现在大三了所以可能会有某些地方写的很冗余
首先,你的先计算出眼睛的一个椭圆方程,这样才好方便接下来的计算,那这时候就得需要根据眼睛的特征点来计算,首先你要知道如果是以dlib 68特征点模型提取人脸特征点的话那么37 ~ 42就是左眼,43 ~ 48就是右眼,这里就以左眼做讲解
我一开始的设计是求出38,42的中点,求出39,41中点,然后以这俩中点作为焦点,然后以三直线相交形成的三角形的中心作为中心
但是后来我发现可以直接拟合这六个特征点求出椭圆方程
Eye = []
for i in range(startIndex, endIndex+1):
# startIndex就是眼睛起始特征点比如左眼就是37,end就是终点
# landmarks_node是提取的68个特征点
Eye.append([landmarks_node[i][0, 0], landmarks_node[i][0, 1]])
ellipseEye = cv2.fitEllipse(np.array(Eye))
# ellipse_Eye[0] 椭圆中心
# ellipse_Eye[1] 短轴和长轴
# 其他属性可以网上自查
然后就可以根据拟合出的椭圆建立椭圆方程,然后计算出椭圆的焦点,焦距,短轴,长轴等基本属性
然后套上面那个圆的公式就好了
代码
import dlib
import cv2
import numpy as np
import math
predictor_path = 'D:/dlib-shape/shape_predictor_68_face_landmarks.dat'
detector = dlib.get_frontal_face_detector()
predictor = dlib.shape_predictor(predictor_path)
def landmark_dec_dlib_fun(img_src):
img_gray = cv2.cvtColor(img_src, cv2.COLOR_BGR2GRAY)
land_marks = []
rects = detector(img_gray, 0)
for i in range(len(rects)):
land_marks_node = np.matrix([[p.x, p.y] for p in predictor(img_gray, rects[i]).parts()])
land_marks.append(land_marks_node)
return land_marks
def getEllipseCross(p1x, p1y, p2x, p2y, a, b, centerX, centerY):
resx = 0
resy = 0
k = (p1y - p2y) / (p1x - p2x);
m = p1y - k * p1x;
A = (b * b + (a * a * k * k))
B = 2 * a * a * k * m
C = a * a * (m * m - b * b)
X1 = (-B + math.sqrt(B * B - (4 * A * C))) / (2 * A)
X2 = (-B - math.sqrt(B * B - (4 * A * C))) / (2 * A)
# Y1 = math.sqrt(1 - (b * b * X1 * X1 ) / (a * a) )
# Y2 = math.sqrt(1 - (b * b * X2 * X2 ) / (a * a) )
Y1 = k * X1 + m
Y2 = k * X2 + m
if getDis(p2x, p2y, X1, Y1) < getDis(p2x, p2y, X2, Y2):
resx = X1
resy = Y1
else:
resx = X2
resy = Y2
return [resx + centerX, resy + centerY]
def getLinearEquation(p1x, p1y, p2x, p2y):
sign = 1
a = p2y - p1y
if a < 0:
sign = -1
a = sign * a
b = sign * (p1x - p2x)
c = sign * (p1y * p2x - p1x * p2y)
return [a, b, c]
def getDis(p1x, p1y, p2x, p2y):
return math.sqrt((p1x - p2x) * (p1x - p2x) + (p1y - p2y) * (p1y - p2y))
def get_line_cross_point(p1x, p1y, p2x, p2y, p3x, p3y, p4x, p4y):
# print(p1x, p1y)
# print(p2x, p2y)
# print(p3x, p3y)
# print(p4x, p4y)
a0, b0, c0 = getLinearEquation(p1x, p1y, p2x, p2y)
a1, b1, c1 = getLinearEquation(p3x, p3y, p4x, p4y)
# print(a0,b0,c0)
# print(a1,b1,c1)
D = a0*b1-a1*b0
if D==0:
return None
x = (b0*c1-b1*c0)/D
y = (a1*c0-a0*c1)/D
return x, y
def localTranslationWarp(srcImg, startIndex, endIndex,Strength,landmarks_node):
midIndex = (startIndex + endIndex + 1) >> 1
startDot = landmarks_node[startIndex]
endDot = landmarks_node[endIndex]
midDot = landmarks_node[midIndex]
Eye = []
for i in range(startIndex, endIndex+1):
Eye.append([landmarks_node[i][0, 0], landmarks_node[i][0, 1]])
ellipseEye = cv2.fitEllipse(np.array(Eye))
# cv2.ellipse(srcImg, ellipseEye, (0, 255, 0), 1)
# cv2.imshow("eli",srcImg)
radius = math.sqrt(
(startDot[0, 0] - midDot[0, 0]) * (startDot[0, 0] - midDot[0, 0]) -
(startDot[0, 1] - midDot[0, 1]) * (startDot[0, 1] - midDot[0, 1])
) / 2
list = []
for i in range(0,3):
tmplist = []
tmplist = get_line_cross_point(
landmarks_node[startIndex + i][0, 0], landmarks_node[startIndex + i][0, 1],
landmarks_node[midIndex + i][0, 0], landmarks_node[midIndex + i][0, 1],
landmarks_node[startIndex + ((i + 1) % 3)][0, 0], landmarks_node[startIndex + ((i + 1) % 3)][0, 1],
landmarks_node[midIndex + ((i + 1) % 3)][0, 0], landmarks_node[midIndex + ((i + 1) % 3)][0, 1]
)
list.append(tmplist)
# for l in list:
# print(l)
a = getDis(list[0][0], list[0][1], list[1][0], list[1][1])
b = getDis(list[1][0], list[1][1], list[2][0], list[2][1])
c = getDis(list[2][0], list[2][1], list[0][0], list[0][1])
centerX = (a * list[0][0] + b * list[1][0] + c * list[2][0]) / (a + b + c)
centerY = (a * list[0][1] + b * list[1][1] + c * list[2][1]) / (a + b + c)
# print(centerX)
# print(centerY)
# print(" ")
width, height, cou = srcImg.shape
Intensity = 15*512*512/(width*height)
ddradius = float(radius * radius)
copyImg = np.zeros(srcImg.shape, np.uint8)
copyImg = srcImg.copy()
K0 = Strength / 100.0
# 计算公式中的|m-c|^2
eyeWidth = radius
eyeHeight = getDis((landmarks_node[startIndex+1][0, 0] + landmarks_node[startIndex+2][0, 0]) / 2,
(landmarks_node[startIndex+1][0, 1] + landmarks_node[startIndex+2][0, 1]) / 2,
(landmarks_node[midIndex+1][0, 0] + landmarks_node[midIndex+2][0, 0]) / 2,
(landmarks_node[midIndex+1][0, 1] + landmarks_node[midIndex+2][0, 1]) / 2)
centerX = ellipseEye[0][0]
centerY = ellipseEye[0][1]
ellipseA = ellipseEye[1][1]
ellipseB = ellipseEye[1][0]
ellipseC = math.sqrt(ellipseA * ellipseA - ellipseB * ellipseB)
# print(ellipseA, ellipseB, ellipseC)
# print(centerX, centerY)
# ddmc = (endX - startX) * (endX - startX) + (endY - startY) * (endY - startY)
#
for i in range(width):
for j in range(height):
# 计算该点是否在形变圆的范围之内
# 优化,第一步,直接判断是会在(startX,startY)的矩阵框中
# if math.fabs(i - centerX) > ((eyeHeight / 2) * 1.5) or math.fabs(j - centerY) > ((eyeWidth / 2) * 1.5):
# continue
if getDis(i, j, centerX - ellipseC, centerY) + getDis(i, j, centerX + ellipseC, centerY) > 2 * ellipseA:
continue
print(i, j)
[crossX, crossY] = getEllipseCross(0, 0, i - ellipseEye[0][0], j - ellipseEye[0][1], ellipseEye[1][1],
ellipseEye[1][0], ellipseEye[0][0], ellipseEye[0][1])
print(crossX, crossY)
radius = getDis(centerX, centerY, crossX, crossY)
ddradius = radius * radius
distance = (i - centerX) * (i - centerX) + (j - centerY) * (j - centerY)
K1 = 1.0 - (1.0 - distance / ddradius) * K0
# 映射原位置
UX = (i - centerX) * K1 + centerX
UY = (j - centerY) * K1 + centerY
print(UX, UY)
# 根据双线性插值法得到UX,UY的值
value = BilinearInsert(srcImg, UX, UY)
# 改变当前 i ,j的值
copyImg[j, i] = value
return copyImg
# 双线性插值法
def BilinearInsert(src, ux, uy):
w, h, c = src.shape
if c == 3:
x1 = int(ux)
x2 = x1 + 1
y1 = int(uy)
y2 = y1 + 1
part1 = src[y1, x1].astype(np.float) * (float(x2) - ux) * (float(y2) - uy)
part2 = src[y1, x2].astype(np.float) * (ux - float(x1)) * (float(y2) - uy)
part3 = src[y2, x1].astype(np.float) * (float(x2) - ux) * (uy - float(y1))
part4 = src[y2, x2].astype(np.float) * (ux - float(x1)) * (uy - float(y1))
insertValue = part1 + part2 + part3 + part4
return insertValue.astype(np.int8)
def face_thin_auto(src,LStrength,RStrength):
landmarks = landmark_dec_dlib_fun(src)
# 如果未检测到人脸关键点,就不进行瘦脸
if len(landmarks) == 0:
return
for landmarks_node in landmarks:
# print(landmarks_node)
bigEyeImage = localTranslationWarp(src,36,41,LStrength,landmarks_node)
bigEyeImage = localTranslationWarp(bigEyeImage,42,47,RStrength,landmarks_node)
cv2.imshow('bigEye', bigEyeImage)
# cv2.imwrite('C:/Users/mibbp/Pictures/bigEye.jpg', bigEyeImage)
def main(LStrength, RStrength):
src = cv2.imread('C:/Users/mibbp/Pictures/bytest.jpg')
cv2.imshow('src', src)
face_thin_auto(src,LStrength,RStrength)
cv2.waitKey(0)
if __name__ == '__main__':
main()
运行结果对比
原图
原版
我的版本
美白算法
这个很简单,这里采用的是白平衡(AWB)算法
YCbCr空间
YUV空间是以前为了解决同时兼容黑白和彩色电视机提出来的,Y指亮度,UV代表颜色分量,黑白电视只显示Y亮度通道就行,而彩色电视则加入颜色分量就行,这里的YCbCr就是如此,其中Y表示亮度,Cb,Cr表示蓝色和红色分量,RGB颜色空间可以和YCbCr互转乘一个矩阵就好了
这里之所以采用YCbCr空间是因为RGB空间里人脸的肤色受亮度影响相当大,所以肤色点很难从非肤色点中分离出来,也就是说在此空间经过处理后,肤色点是离散的点,中间嵌有很多非肤色,这为肤色区域标定(人脸标定、眼睛等)带来了难题。如果把RGB转为YCrCb空间的话,可以忽略Y(亮度)的影响,因为该空间受亮度影响很小,肤色会产生很好的类聚。这样就把三维的空间降为二维的CrCb,肤色点会形成一定得形状,如:人脸的话会看到一个人脸的区域,手臂的话会看到一条手臂的形态,对处理模式识别很有好处,根据经验某点的CrCb值满足:133≤Cr≤173,77≤Cb≤127 那么该点被认为是肤色点,其他的就为非肤色点。
灰色世界算法
灰色世界假设:任意一副图像,当它有足够的色彩变化,则它的RGB分量的均值会趋于相等
这是一个假设,灰色世界算法就是基于这个假设的,写起来也是真的简单
∵ R m e a n = G m e a n = B m e a n 以 G 为 基 准 算 法 R , B 的 增 益 ∴ R g a i n = G m e a n R m e a n ∴ B g a i n = G m e a n B m e a n ∴ R ′ = R ⋅ R g a i n ∴ B ′ = B ⋅ B g a i n \because R_{mean} = G_{mean} = B_{mean} \\ 以G为基准算法R,B的增益 \\ \therefore R_{gain} = \frac{G_{mean}}{R_{mean}} \\ \therefore B_{gain} = \frac{G_{mean}}{B_{mean}} \\ \therefore R' = R\cdot R_{gain} \\ \therefore B' = B\cdot B_{gain} ∵Rmean=Gmean=Bmean以G为基准算法R,B的增益∴Rgain=RmeanGmean∴Bgain=BmeanGmean∴R′=R⋅Rgain∴B′=B⋅Bgain
完美反射算法
完美反射算法基于这样一种假设,一幅图像中最亮的像素相当于物体有光泽或镜面上的点,它传达了很多关于场景照明条件的信息。如果景物中有纯白的部分,那么就可以直接从这些像素中提取出光源信息。因为镜面或有光泽的平面本身不吸收光线,所以其反射的颜色即为光源的真实颜色,这是因为镜面或有光泽的平面的反射比函数在很长的一段波长范围内是保持不变的。完美反射法就是利用用这种特性来对图像进行调整。算法执行时,检测图像中亮度最高的像素并且将它作为参考白点。基于这种思想的方法都被称为是完美反射法也称镜面法。
R g a i n = m a x ( R m a x , G m a x , B m a x ) R m a x G g a i n = m a x ( R m a x , G m a x , B m a x ) G m a x B g a i n = m a x ( R m a x , G m a x , B m a x ) B m a x R_{gain} = \frac{max(R_{max},G_{max},B_{max})}{R_{max}} \\ G_{gain} = \frac{max(R_{max},G_{max},B_{max})}{G_{max}} \\ B_{gain} = \frac{max(R_{max},G_{max},B_{max})}{B_{max}} Rgain=Rmaxmax(Rmax,Gmax,Bmax)Ggain=Gmaxmax(Rmax,Gmax,Bmax)Bgain=Bmaxmax(Rmax,Gmax,Bmax)
动态阈值法
- 将图像从RGB空间变换到YCrCb空间
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \begin{bmatri…
-
白点检测:为了增强算法的鲁棒性,将图像分为12部分
-
计算每个区域的 C r , C b C_r,C_b Cr,Cb的均值 M r , M b M_r,M_b Mr,Mb,N为每块区域的像素个数:
M r = ∑ C r ( i , j ) N , M b = ∑ C b ( i , j ) N M_r = \frac {\sum C_r(i,j)}{N},M_b = \frac {\sum C_b(i,j)}{N} Mr=N∑Cr(i,j),Mb=N∑Cb(i,j) -
计算每个区域的Cr,Cb分量的绝对偏差的均值Dr,Db:
D r = ∑ ∣ C r ( i , j ) − M r ∣ N , D b = ∑ ∣ C b ( i , j ) − M b ∣ N D_r = \frac {\sum \vert C_r(i,j) - M_r\vert }{N},D_b = \frac {\sum \vert C_b(i,j) - M_b\vert }{N} Dr=N∑∣Cr(i,j)−Mr∣,Db=N∑∣Cb(i,j)−Mb∣
-
-
最后整幅图像的均值 Mb,Mr 以及方差 Db,Dr 由除去T条件c后剩下的块计算平均值得到。
-
选择候补白点,若某像素满足一下条件:
C b ( i , j ) − ( M b + D b × s i g n ( M b ) ) < ∣ 1.5 × D b ∣ C b ( i , j ) − ( 1.5 × M r + D r × s i g n ( M r ) ) < ∣ 1.5 × D r ∣ C_b(i,j)-(M_b+D_b\times sign(M_b)) < \vert 1.5 \times D_b \vert \\ C_b(i,j)-(1.5 \times M_r+D_r\times sign(M_r)) < \vert 1.5 \times D_r \vert Cb(i,j)−(Mb+Db×sign(Mb))<∣1.5×Db∣Cb(i,j)−(1.5×Mr+Dr×sign(Mr))<∣1.5×Dr∣ -
然后根据候补白点的像素亮度值由高到低排列,从候补白点中选取亮度值在前 10%的白点做为参考白点。白平衡的增益值就是根据选取的参考白点确定的。
-
为了让校正后的图像亮度跟校正前的图像亮度保持在同一水平,在增益计算时采用最大的亮度值作为参考。增益系数的计算公式公式如下:
R g a i n = Y m a x R a v g w , G g a i n = Y m a x G a v g w , B g a i n = Y m a x B a v g w R_{gain}= \frac {Y_{max}} {R_{avgw}},G_{gain}= \frac {Y_{max}} {G_{avgw}},B_{gain}= \frac {Y_{max}} {B_{avgw}} Rgain=RavgwYmax,Ggain=GavgwYmax,Bgain=BavgwYmax
function results = SkinWhitening(app,Img)
value = app.Slider_29.Value;
im = Img;
im1=rgb2ycbcr(im);%将图片的RGB值转换成YCbCr值%
YY=im1(:,:,1);
Cb=im1(:,:,2);
Cr=im1(:,:,3);
[x, y, z]=size(im);
tst=zeros(x,y);
Mb=mean(mean(Cb));
Mr=mean(mean(Cr));
%计算Cb、Cr的均方差%
Tb = Cb-Mb;
Tr = Cr-Mr;
Db=sum(sum((Tb).*(Tb)))/(x*y);
Dr=sum(sum((Tr).*(Tr)))/(x*y);
%根据阀值的要求提取出near-white区域的像素点%
cnt=1;
for i=1:x
for j=1:y
b1=Cb(i,j)-(Mb+Db*sign(Mb));
b2=Cr(i,j)-(1.5*Mr+Dr*sign(Mr));
if (b1<abs(1.5*Db) && b2<abs(1.5*Dr))
Ciny(cnt)=YY(i,j);
tst(i,j)=YY(i,j);
cnt=cnt+1;
end
end
end
cnt=cnt-1;
iy=sort(Ciny,'descend');%将提取出的像素点从亮度值大的点到小的点依次排列%
nn=round(cnt/10);
Ciny2(1:nn)=iy(1:nn);%提取出near-white区域中10%的亮度值较大的像素点做参考白点%
%提取出参考白点的RGB三信道的值%
mn=min(Ciny2);
for i=1:x
for j=1:y
if tst(i,j)<mn
tst(i,j)=0;
else
tst(i,j)=1;
end
end
end
R=im(:,:,1);
G=im(:,:,2);
B=im(:,:,3);
R=double(R).*tst;
G=double(G).*tst;
B=double(B).*tst;
%计算参考白点的RGB的均值%
Rav=mean(mean(R));
Gav=mean(mean(G));
Bav=mean(mean(B));
Ymax=double(max(max(YY)))*0.15;%计算出图片的亮度的最大值%
%计算出RGB三信道的增益%
Rgain=Ymax/Rav;
Ggain=Ymax/Gav;
Bgain=Ymax/Bav;
%通过增益调整图片的RGB三信道%
im(:, :, 1)=im(:, :, 1) * Rgain * (value / 5);
im(:, :, 2)=im(:, :, 2) * Ggain * (value / 5);
im(:, :, 3)=im(:, :, 3) * Bgain * (value / 5);
results = im;
end
结果
唇彩算法
唇彩算法本质上很简单,就是把嘴唇那个区域染成合适的颜色就好了,但是实际上的处理还是很复杂的,不过还好上学期学的计算机图形学学了相应的算法和数据结构
四转八联通种子填充
种子填充算法本质就是BFS,DFS搜索(和本次实验无关:关于搜索我在B站也有录视频讲过链接),这个在之前的数据结构课是学了的就是广度优先和深度优先,不过老师发的源码让我不能理解的就是他是用栈实现的BFS,因为一般BFS都是队列或者优先队列实现DFS才是递归用栈。
这里我主要说如何用BFS实现。
四联通
种子填充算法主要流程是这样的:
- 将种子点入队。如果队列为空,则转 3,否则转 2
- 从队头取出一个元素(也就是一个点),并将该点置成填充色,并判断该像素相邻的四连接点是否为边界色或已经置为多边形的填充色,若不是,则将该点入队。转 2)
- 结束。
如果你能理解上面流程那直接往下看,不理解的话我解释一下一些名词。
四联通或者说四连接就一个点的上下左右四个点
那你现在再回去看看算法流程就是,先确定一个起始点我们称为种子点(要在填充图形内部),将他先入队,然后每次从队列取出队头元素,将其上色,然后判断这个点的上下左右四个点,看是否满足条件(不是边界点,且没有上色)如果满足将他入队,然后一直这样下去直到队列为空。
用队列的原因就是因为可以将不用的点弹出优化空间,减少内存消耗,不用栈是因为他容易爆而且他先进后出(他凭什么后来居上),如果内存不够就手动调一下堆栈内存或者开全局,全局变量放在堆里的内存管够
八联通
八联通和四联通一样就是四个方向多了个左上,左下,右上,右下,
为啥要这样啊因为有这种特殊情况
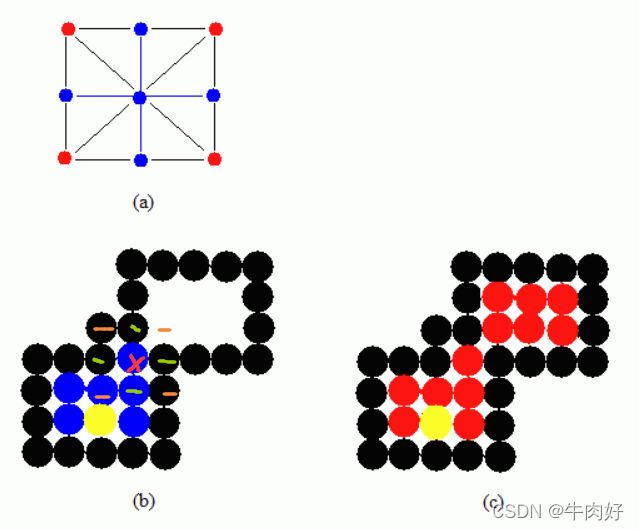
对于左边那个x点绿色是四联通到的点,橙色是八联通能额外到的点,四联通到不了左上角的空白区域所以无法填充,而八联通可以,右边就是八联通填充效果。
八联通就放向多加四个就行,就这么简单,但是这样也会变慢很多,因为他每次扩展多扩展了一倍
优化种子填充算法
我接下来说的就是我写的优化版本了,如果只是应付实验报告的话,用老师的代码套上面我写的就行。
在我写的时候有个bug不过懒得找反正能跑,而且结果对。
我这里主要优化除了刚刚用BFS队列去优化以外,还实现了四联通转八联通的优化,外加哈希表存储已填充的点。
四联通转八联通
之所以用八联通就是无法处理上述那种特殊情况,但是八联通很慢也很占内存,因为扩展了八个点,所以我设想能否去优化四联通去实现这种特殊情况,我这里用的方法是四联通但是方向不是上下左右,而是左上左下右上右下四个方向,然后一开始引入两个相邻种子点,为什么呢,看图:

1,2点是一开始入队的两个相邻种子点,黑色点是2好点四联通扩展出的所有点,白色点是1号点四联通扩展出的所有点,所以我们只用了四联通却实现了八联通的效果。切实际情况测试下来,每次扩展其实平均在两次(手动模拟一下就知道了),从八降到了二,无论是空间还是时间都是质的提升。
边界处理
对于向外扩展的点判断其是否是在填充图形内可以参考之前的有效边表的处理,内部点才入队将其上色
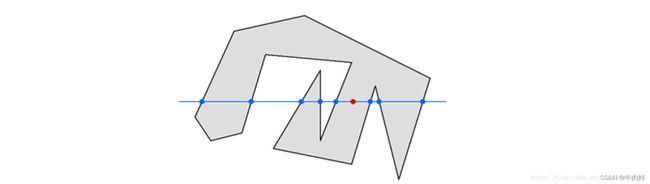
奇-偶规则(Odd-even Rule)
从任意位置p作一条射线,若与该射线相交的多边形边的数目为奇数,则p是多边形内部点,否则是外部点。
非零环绕数规则(Nonzero Winding Number Rule)
首先使多边形的边变为矢量。
将环绕数初始化为零。
再从任意位置p作一条射线。当从p点沿射线方向移动时,对在每个方向上穿过射线的边计数,每当多边形的边从右到左穿过射线时,环绕数加1,从左到右时,环绕数减1。
处理完多边形的所有相关边之后,若环绕数为非零,则p为内部点,否则,p是外部点。
这个就是个拓展主要处理区域重叠。
代码
"""
作者:Mibbp
日期: 2022年11月02日
"""
# encoding:utf-8
from collections import deque
import dlib
import numpy as np
import cv2
def resize(image, width=600):
r = width * 1.0 / image.shape[1]
dim = (width, int(image.shape[0] * r))
resized = cv2.resize(image, dim, interpolation=cv2.INTER_AREA)
return resized
def rect_to_bb(rect):
x = rect.left()
y = rect.top()
w = rect.right() - x
h = rect.bottom() - y
return x, y, w, h
def getbgr(image, xx, yy):
bb = 0
gg = 0
rr = 0
bgr = image[yy, xx]
for ii in range(-1, 1):
for jj in range(-1, 1):
if ii == 0 and jj == 0:
continue
tx = xx + ii
ty = yy + jj
tbgr = image[ty, tx]
bb += tbgr[0]
gg += tbgr[1]
rr += tbgr[2]
bb = int(bb / 8 / 3 + bgr[0] / 3 * 2)
gg = int(gg / 8 / 3 + bgr[1] / 3 * 2)
rr = int(rr / 8 / 3 + bgr[2] / 3 * 2)
print(bb, gg, rr)
return bgr
def shape_to_np(shape, dtype="int"):
coords = np.zeros((68, 2), dtype=dtype)
for i in range(0, 68):
coords[i] = (shape.part(i).x, shape.part(i).y)
return coords
def bfs(image, edge_list, convex):
que = deque()
dis = np.zeros((image.shape[0], image.shape[1]), dtype=int)
for node in edge_list:
que.append((node[0], node[1]))
dis[node[0], node[1]] = -10
cc = 0
while que:
cc += 1
now = que.popleft()
# nbgr = image[now[1], now[0]]
if dis[now[0], now[1]] + 1 < 0:
for xx in range(-1, 1):
for yy in range(-1, 1):
ty = yy + now[1]
tx = xx + now[0]
if cv2.pointPolygonTest(convex, (tx, ty), False) < 0:
if dis[tx, ty] > dis[now[0], now[1]] + 1:
dis[tx, ty] = dis[now[0], now[1]] + 1
tbgr = image[ty, tx]
if tbgr[0] + 40 < 255:
image[ty, tx][0] = tbgr[0] + 40
if tbgr[1] - 10 < 255:
image[ty, tx][1] = tbgr[1] - 10
if tbgr[2] - 10 < 255:
image[ty, tx][2] = tbgr[2] - 10
if (tx, ty) not in que:
que.append((tx, ty))
print(cc)
return image
def outside_edge_judge(x, y, d1, d2, edgelist, threshold, img):
a1 = 1 if -threshold <= d1 <= threshold else 0
a2 = 1 if -threshold <= d2 <= threshold else 0
if a1 + a2 == 1:
edgelist.append([y, x])
return True
return False
def inside_edge_judge(x, y, d1, edgelist, threshold, img):
a = 1 if -threshold <= d1 <= threshold else 0
if a == 1:
edgelist.append([y, x])
return True
return False
def mouth_area_rect(points):
mins = points.min(axis=0)
maxs = points.max(axis=0)
return mins[0], maxs[0] + 1, mins[1], maxs[1] + 1
def most_frequently_hsv(img, array):
arr = []
for pixel in array:
yy = pixel[0]
xx = pixel[1]
ph = img[yy, xx][0]
ps = img[yy, xx][1]
pv = img[yy, xx][2]
arr.append([ph, ps, pv])
arr = np.array(arr)
h = np.argmax(np.bincount(arr[:, 0]))
s = np.argmax(np.bincount(arr[:, 1]))
v = np.argmax(np.bincount(arr[:, 2]))
return int(h), int(s), int(v)
def color_delta(c1, c2):
c1 = np.array(c1)
c2 = np.array(c2)
delta = c1 - c2
return np.max(delta) - np.min(delta)
def exact_lip_points(img, all_points, color):
color = np.array(color)
exact_points = []
delta = 20
for pixel in all_points:
pixel_hsv = np.array(img[pixel[0], pixel[1]])
if color_delta(color, pixel_hsv) < delta:
exact_points.append(pixel)
return exact_points
def side_edge_move(edge_points_array, type, color, min_delta, max_delta, min_e, max_e, img):
res = {}
rgb_color = (154, 107, 113)
# color=(rgb_color[0]*180,rgb_color[1]*255,rgb_color[2]*255)
if type == 'outside':
type = 1
elif type == 'inside':
type = -1
else:
type = 0
# 首先找出每一列的两个边界点 [0]是上边界,[1]是下边界
for px in edge_points_array:
x = px[1]
y = px[0]
if x in res.keys():
if y < res[x][0]:
res[x][0] = y
if y > res[x][1]:
res[x][1] = y
else:
res[x] = [y, y]
# 确保每列都有上下两个边界
for x, yrange in res.items():
if res[x][0] == res[x][1]:
if x + 1 in res.keys():
res[x][0] = res[x + 1][0]
res[x][1] = res[x + 1][1]
else:
res[x][0] = res[x - 1][0]
res[x][1] = res[x - 1][1]
# 遍历每个边界
if type != 0:
for x, yrange in res.items():
direction = 0 if type == 1 else 1
upside_hsv = img[yrange[direction], x] # 外边缘是上边界,内边缘是下边界
e = 0
# 外边缘上边界在嘴唇,则向上逃离
# 内边缘下边界在嘴唇,也向上逃离
while color_delta(color, upside_hsv) - min_delta < 0 and e > -min_e:
e -= 1
upside_hsv = img[yrange[direction] + e, x]
# 外边缘上边界在外部,则向下靠拢
# 内边缘下边界在外部,也向下靠拢
while color_delta(color, upside_hsv) - max_delta > 0 and e < max_e:
e += 1
upside_hsv = img[yrange[direction] + e, x]
res[x][direction] = yrange[direction] + e
direction = 1 - direction
downside_hsv = img[yrange[direction], x] # 外边缘是下边界,内边缘是上边界
e = 0
# 外边缘下边界在嘴唇,则向下逃离
# 内边缘上边界在嘴唇,也向下逃离
while color_delta(color, downside_hsv) - min_delta < 0 and e < min_e:
e += 1
downside_hsv = img[yrange[direction] + e, x]
# 外边缘下边界在外部,则向上靠拢
# 内边缘上边界在外部,也向上靠拢
while color_delta(color, downside_hsv) - max_delta > 0 and e > -max_e:
e += -1
downside_hsv = img[yrange[direction] + e, x]
res[x][direction] = yrange[direction] + e
return res
def outline(res, img, color):
for x, yrange in res.items():
img[yrange[0], x] = (0, 0, 0)
img[yrange[1], x] = (0, 0, 255)
def padding_inside_points(pts, edge_points):
# 0,12为左侧两嘴角
# 6,16为右侧两嘴角
left_x1 = pts[0][0]
left_x2 = pts[12][0]
y = pts[12][1]
for x in range(left_x1, left_x2):
edge_points.append([y, x])
right_x1 = pts[16][0]
right_x2 = pts[6][0]
y = pts[16][1]
for x in range(right_x1, right_x2):
edge_points.append([y, x])
def draw_Convex(image,hull,color):
length = len(hull)
for i in range(len(hull)):
cv2.line(image, tuple(hull[i][0]), tuple(hull[(i + 1) % length][0]), color, 2)
def feature(path, color, outside_tuple=(40, 50, 3, 2), inside_tuple=(90, 100, 3, 1)):
(a1, a2, a3, a4) = outside_tuple
(b1, b2, b3, b4) = inside_tuple
detector = dlib.get_frontal_face_detector() # [cy]:人脸检测仪
predictor = dlib.shape_predictor("D:/dlib-shape/shape_predictor_68_face_landmarks.dat") # [cy]:关键点检测器
image = cv2.imread(path) # [cy]:读取 输入图像.jpg
image = resize(image, width=600) # [cy]:缩放 图像,宽为1200
print(image.shape) # [cy]:image尺寸 (高,宽,3)
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY) # [psy]:转为灰度图
# 传入灰度图像,检测出里面的所有脸,某张脸的矩形:rect=[(左上角坐标),(右下角坐标)]
# OpenCV坐标
# (0,0) - (100,0)
# | |
# (0,100) - (100,100)
rects = detector(gray, 1) # [psy]:灰度图里定位人脸
shapes = [] # [psy]:shapes存储找到的人脸框,人脸框仅包含四个角数值如frontal_face_detector.png所示。
for (i, rect) in enumerate(rects): # 遍历所有脸的方框
shape = predictor(gray, rect) # 用关键点检测器检测出关键点们
shape = shape_to_np(shape) # 关键点们变成numpy数组
shape = shape[48:] # 关键点[48-67]是嘴唇区域
# print(shape)
shapes.append(shape) # 把这张脸的嘴唇关键点插入到shapes
# print("111")
# 图片转为hsv形式,色调(H),饱和度(S),亮度(V)
# H: 0 — 180
# S: 0 — 255
# V: 0 — 255
image = cv2.cvtColor(image, cv2.COLOR_BGR2HSV)
for shape in shapes:
# 遍历每个嘴唇
# 获取嘴唇像素的矩形
xstart, xend, ystart, yend = mouth_area_rect(shape)
# 图像的高与宽
# sx, sy = image.shape[0], image.shape[1]
# 外嘴唇左半边凸包
hull_left = cv2.convexHull(np.concatenate((shape[0:4], shape[7:12])))
# print(hull_left)
# color = (0,255,0)
# draw_Convex(image,hull_left,color)
# 外嘴唇右半边凸包
hull_right = cv2.convexHull(shape[3:8])
# color = (0,125,0)
# draw_Convex(image,hull_right,color)
# 内嘴唇凸包
hull_inside = cv2.convexHull(shape[12:])
# for i in range(12,19):
# print(shape[i])
# print(("111"))
# print(hull_inside)
color = (0,200,0)
draw_Convex(image,hull_inside,color)
# 嘴唇外边缘上的点
outside_edge_points = []
# 嘴唇内边缘上的点
inside_edge_points = []
# 嘴唇上的所有点
lip_points = []
for xx in range(xstart, xend):
for yy in range(ystart, yend):
# 获得(xx,yy)到左外凸包的距离,正数说明在内部,measureDist:是否返回准确距离
dist_left = cv2.pointPolygonTest(hull_left, (xx, yy), measureDist=True)
# 获得(xx,yy)到右外凸包的距离,正数说明在内部,measureDist:是否返回准确距离
dist_right = cv2.pointPolygonTest(hull_right, (xx, yy), measureDist=True)
# 获得(xx,yy)到内凸包的距离,正数说明在内部,measureDist:是否返回准确距离
dist_inside = cv2.pointPolygonTest(hull_inside, (xx, yy), measureDist=True)
# 判断在外边缘则加入边缘点集
outside_edge_judge(xx, yy, dist_left, dist_right, outside_edge_points, 0.5, image)
# 判断在内边缘则加入边缘点集
inside_edge_judge(xx, yy, dist_inside, inside_edge_points, 1, image)
# (在外嘴唇左凸包以内或在外嘴唇右凸包以内)且在内嘴唇凸包以外为嘴唇
if dist_left >= -0.5 or dist_right >= -0.5:
if dist_inside < 20:
lip_points.append([yy, xx])
often_color = most_frequently_hsv(image, lip_points) # 得到最频繁的颜色组合
outside_edge_points = side_edge_move(outside_edge_points, 'outside', often_color, a1, a2, a3, a4, image)
padding_inside_points(shape, inside_edge_points) # [cy]:补齐内边缘点,以内嘴角和外嘴角之间为准
inside_edge_points = side_edge_move(inside_edge_points, 'inside', often_color, b1, b2, b3, b4, image)
# cv2.rectangle(image, (xstart, ystart-100), (xend, yend-100), often_color, thickness=2) # 显示在图像上
for pixel in lip_points:
yy = pixel[0]
xx = pixel[1]
on_lip = False
if xx in inside_edge_points.keys():
if outside_edge_points[xx][0] < yy < inside_edge_points[xx][0] or \
inside_edge_points[xx][1] < yy < outside_edge_points[xx][1]:
on_lip = True
else:
if outside_edge_points[xx][0] < yy < outside_edge_points[xx][1]:
on_lip = True
if on_lip:
image[yy, xx][0] = color[0]
image[yy, xx][1] = color[1]
# image[yy, xx][2] += 10
# outline(outside_edge_points, image, often_color)
# outline(inside_edge_points, image, often_color)
# for pixel in exact_points:
# yy = pixel[0]
# xx = pixel[1]
# image[yy, xx][0] = color[0]
# image[yy, xx][1] = color[1]
# image[yy, xx][2] = 255
# for pixel in shape:
# xx = pixel[0]
# yy = pixel[1]
# image[yy, xx][0] = 0
# image[yy, xx][1] = 0
# image[yy, xx][2] = 255
image = cv2.cvtColor(image, cv2.COLOR_HSV2BGR)
# image = cv2.GaussianBlur(image, (7, 7), 0)
# shape=shapes[0]
# polygon1 = np.concatenate((shape[0:4], shape[7:12])) # 48 49 50 51 55 56 57 58 59
# polygon2 = shape[3:8] # 51 52 53 54 55
# cv2.polylines(image, [polygon1], True, (0, 0, 0), 2)
# cv2.polylines(image, [polygon2], True, (0, 0, 250), 2)
return image
def update(h,s):
input_image_path = "C:/Users/mibbp/Pictures/sl2.jpg" # 输入图像.jpg
lipstick_color = [h,s, 0] # [cy]:嘴唇颜色
image_output = feature(input_image_path, lipstick_color) # 处理图像
cv2.imshow("output", image_output) # 显示 输出图像2.jpg
# cv2.imwrite("C:/Users/mibbp/Pictures/Lipstickoutput.jpg" , image_output) # 保存 输出图像2.jpg
# cv2.waitKey(0)
def nothing(x):
pass
def test():
print('Lipstick11')
def main():
h=170
s=220
if(h>180):
h-=180
update(h,s)
cv2.waitKey(0)
if __name__=="__main__":
main()
彩妆迁移
超像素
算法原理
原论文
SRCNN
代码
%% read ground truth image
im = imread('C:/Users/mibbp/Pictures/sl2.jpg');
%im = imread('Set14\zebra.bmp');
%% set parameters
up_scale = 3;
model = 'D:/数值图像分析/SRCNN/model/9-5-5(ImageNet)/x3.mat';
% up_scale = 3;
% model = 'model\9-3-5(ImageNet)\x3.mat';
% up_scale = 3;
% model = 'model\9-1-5(91 images)\x3.mat';
% up_scale = 2;
% model = 'model\9-5-5(ImageNet)\x2.mat';
% up_scale = 4;
% model = 'model\9-5-5(ImageNet)\x4.mat';
%% work on illuminance only
if size(im,3)>1
im = rgb2ycbcr(im);
im = im(:, :, 1);
end
im_gnd = modcrop(im, up_scale);
im_gnd = single(im_gnd)/255;
%% bicubic interpolation
im_l = imresize(im_gnd, 1/up_scale, 'bicubic');
im_b = imresize(im_l, up_scale, 'bicubic');
%% SRCNN
im_h = SRCNN(model, im_b);
%% remove border
im_h = shave(uint8(im_h * 255), [up_scale, up_scale]);
im_gnd = shave(uint8(im_gnd * 255), [up_scale, up_scale]);
im_b = shave(uint8(im_b * 255), [up_scale, up_scale]);
%% compute PSNR
psnr_bic = compute_psnr(im_gnd,im_b);
psnr_srcnn = compute_psnr(im_gnd,im_h);
%% show results
fprintf('PSNR for Bicubic Interpolation: %f dB\n', psnr_bic);
fprintf('PSNR for SRCNN Reconstruction: %f dB\n', psnr_srcnn);
subplot(1,2,1), imshow(im_b); title('Bicubic Interpolation');
subplot(1,2,2), imshow(im_h); title('SRCNN Reconstruction');
imwrite(im_b, ['Bicubic Interpolation' '.bmp']);
imwrite(im_h, ['SRCNN Reconstruction' '.bmp']);
交互式瘦脸
这个原理和上面那个一样就是不需要人脸检测了所以更简单,但是代码有点Bug,太忙了实在是不想改了
代码
for cou =1:300
if cou==1
I = imread('C:/Users/mibbp/Pictures/pysltest.jpg');%读入图片
else
I = imread('C:/Users/mibbp/Pictures/pltest.jpg');
end
figure
imshow(I);
h = drawcircle('Color','k','FaceAlpha',0.4);
M = ginput(1);
[m,n,~] = size(I);
center = [floor(h.Center(2)),floor(h.Center(1))];%变形前的圆心
radius = h.Radius;%变形的圆半径
RGB_buff = I;
%遍历圆形选区的每一个像素
for i=1:m
for j=1:n
distant = sqrt((i-center(1)).^2+(j-center(2)).^2);
if distant <= radius
% R_buff = I(i,j,1);
% G_buff = I(i,j,2);
% B_buff = I(i,j,3);
x = [i,j];%变形后的坐标
U = x - ((radius^2 - (x - center).^2) / (radius^2 - (x - center).^2 + (M - center).^2))^2 * (M - center);%逆变换公式
% K1 = real(sqrt( (x(1) - center(1))^2 + (x(2) - center(2))^2) );
% U = real(x - U*(1.0-K1/radius));
% if(U(1)<0||U(2)<0)
% continue;
% end
% center
% x
% U
%用双线性插值算出U所在的位置的RGB分量
% A = [real(round(U(1)-0.5)),real(round(U(2)-0.5))];
% B = [real(round(U(1)+0.5)),real(round(U(2)-0.5))];
% C = [real(round(U(1)-0.5)),real(round(U(2)+0.5))];
% D = [real(round(U(1)+0.5)),real(round(U(2)+0.5))];
%
% RGBE = I(A(1),A(2)) + (U(1)-A(1)) * (I(B(1),B(2))-I(A(1),A(2)));
% RGBF = I(C(1),C(2)) + (U(1)-C(1)) * (I(D(1),D(2))-I(C(1),C(2)));
% % I(x);
% I(x) = RGBE + (U(2)-A(2)) * (RGBF - RGBE);
% % I(x);
uu = floor(U);
ab = U-uu;
a = ab(1);
b = ab(2);
m1 = uu(1);
n1 = uu(2);
for k=1:3
I(i,j,k)=(1-a)*(1-b)*RGB_buff(m1,n1,k)+a*(1-b)*RGB_buff(m1+1,n1,k)+(1-a)*b*RGB_buff(m1,n1,k)+a*b*RGB_buff(m1+1,n1+1,k);
end
end
end
end
figure
imshow(I);
answer = questdlg('是否要继续调整', ...
'选择', ...
'YES','NO','NO');
switch answer
case 'YES'
imwrite(I,"C:/Users/mibbp/Pictures/pltest.jpg");
case 'NO'
msgbox("退出调整");
break;
end
end
四、创新点
整体设计框架不知道有没有人和我想的一样,但是效果很好,可扩展性也很高
大眼算法算是比较创新的,其他的都是有原算法或者论文的,这个大眼应该找不到跟我一样的可能
四转八联通填充也算是我想出来的,但是也可能早就有人想出来了毕竟不难
不太清楚创新点定义是啥,如果要是没啥人发现的话那可能就这些了
五、心得体会
就用到的算法都不简单,也学了很多新的算法,但是本质上都是一些学过的算法和数据结构的应用,一开始想做的是车牌识别因为很简单,后面发现没人做出来美图秀秀,所以想了想还是做出来一个能让大家参考一下,虽然用时很短只做了不到一周但是学了很多东西,一开始也比较迷茫不清楚做什么功能,看了美图秀秀软件感觉也没啥功能,主要就是瘦脸美白那些,即使知道了做啥也不清楚具体怎么做,只能网上大量搜索相关博客和具体算法的论文来学习,前几天就是各种看论文理解算法思路,努力看懂实现代码的逻辑
虽然最终做出来的效果一般,但是好在也学到了不少新东西