申明:全为我今天所学的知识的简单总结,内容可能比较乱。只是为了做简单的知识的回顾和总结,可能有些知识点也可以帮助解决遇到的问题。
1.pandas.read_csv()读取CSV文件。在excel文件保存的时候可以保存为csv文件。
2.pandas.value_counts(data["列名“],sort=True).sort_index() 读出该列中不同属性值分别对应的个数
3.样本不均衡怎么办(比如说百分之90就是都是属于0类,百分之10属于1类),过采样和下采样。
下采样:对于不均衡数据变成均衡数据,让属于0类和1类的一样少。
过采样:将少的样本生成一些数据,使得0类和1类的数据一样多。
4.From sklearn.preprocessing import StandardScaler(标准化数据,对于一些数据跟其他比起来比较大或者不规律,先标准化到0-1之间
data['新列名’]=StandardScaler().fit_transform(data['列名‘].reshape(-1,1))将想要标准化的那一列就行标准化,并且会新生成一个列,可以定义一个新的列名。reshape()一列,多少行让程序自己去计算
data.drop['列名'].axis=0 ....(///
data.ix[:,data.columns!='列名’]DataFrame中的ix操作先行后列,式子中表示所有行,但是不取指定的列。
5.np.random.choice(在哪选,选多少,是否可以代替)从数据中随机选出一定数量的结果
np.concatenate()将数据进行合并
6.交叉验证:(先对数据进行洗牌)去除数据的规律性
对数据进行切分,训练数据和测试数据进行切分(当然这的测试数据只是为了交叉验证,和广义的测试数据不一样。现在的所有切分都是在训练数据上进行的)
假设分为三份A,B,C
首先用A+B进行训练模型,然后用C来测试参数。 其次用A+C训练模型,用B来测试参数。
最后用B+C进行训练模型,然后用A来测试参数 (交叉验证是为了验证参数,当有几个参数可选的时候用这个来验证,也可以分为5段等)最后使数据尽量平稳不会太高也不会太低。
From sklearn.cross_validation import train_test_split#引入切分数据
为什么在下采样的时候还要对原数据进行切分,因为下采样的数据训练完的模型是要用原数据的测试数据来进行测试,不是拿下采样数据的测试数据来测试,毕竟量太少了。。
7.建模:逻辑回归
精度:真实值和预测值进行比较,相等的总的数量比上所有的数量。
有些情况下,精度很高,但是没什么实际作用。预测癌症,大家都预测出来没毛病。但是其实我们是想要预测出来的。 所以精度会骗人。
recall:召回率。还是用癌症的例子说明。比方一共100人,10个有癌症。我们想要检测出癌症的就是这10个人。召回率就是说最后我们检测出来的人数比上我们想要检测的总人数在这里也就是10.(使用更多)
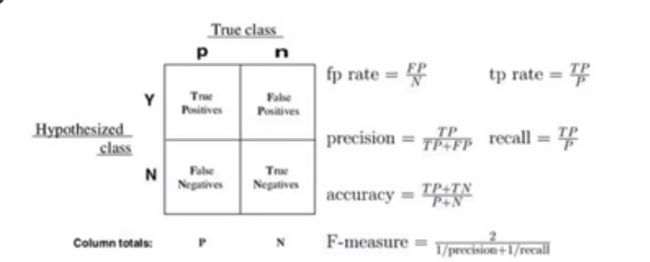
召回率=TP/TP+FN (混淆矩阵马上说)
相关正类:TP 就是把本来是正例的预测成了正例 无关负类:FP 把本来是负类预测称了正类
FN :正类判定为负类 TN:负类判定为负类。(个数)
From sklearn.linear_model import LogiticRsgression#逻辑回归
From sklearn.cross_validation import KFold(这个数表示做几倍的交叉验证)
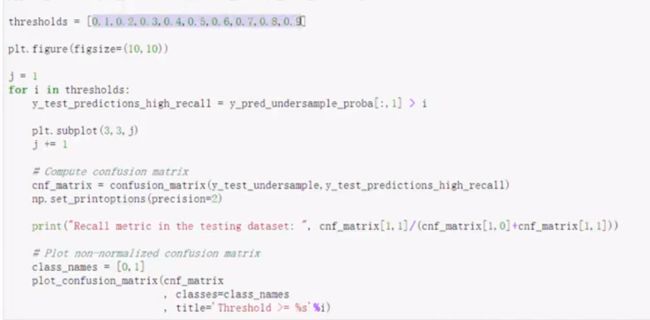
cross_val_score评估结果 根据不同的threshold来画混淆矩阵
正则化:
在召回率相同的情况下,判断模型的参数值太过于浮动不行,需要稳定,防止过拟合危险。
正则化惩罚项:大力惩罚波动较大的参数模型
loss损失函数+1/2W的平方加上惩罚函数,越不稳定,loss越大,加上惩罚函数再来比较两个参数模型。
L2正则化加的1/2W的平方 L1正则化直接加W的绝对值
可以在L1和L2前加倍数。λL2的λ等于多少效果会更好,可以以通过交叉验证来评估。
逻辑回归模型LogisticRegression(C=(惩罚系数λ),正则化类型L1或者L2)
用交叉验证出来的值去训练模型
recall_score()计算召回率
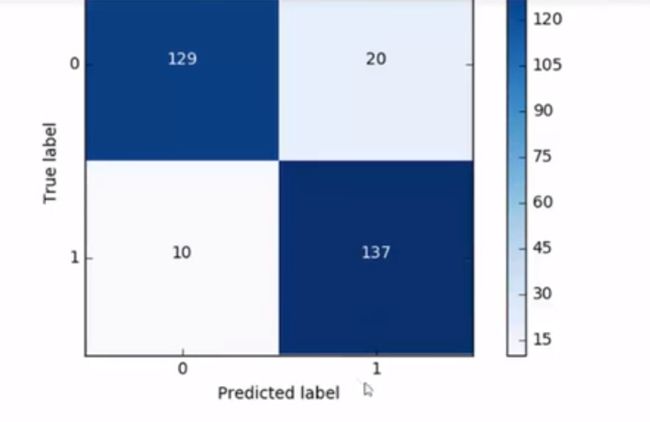
8.混淆矩阵
x轴为预测值,Y轴为真实值,来计算衡量指标recal和精度
9.下采样法,才通过混淆矩阵可以看到,召回率是高了,但是导致有许多被误杀的,预测错了/使得精度降低,这是下采样的潜在问题。
10.过采样:
SMOTE样本生成策略。对于少数类的每一个样本,以欧氏距离为标准计算他到少数类样本集总所有样本的距离,使得到其K近邻
确定采样倍率。 假设五倍。 选择d1到d5(这些都是x的k近邻),用公式构建样本。
对于d1到d5:Xnew=x+rand(0,1)×(x(上边有波浪)-x)表示二者之间的距离
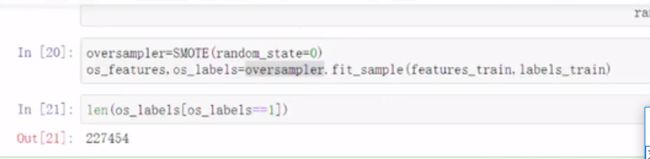
引入SMOTE:FROM imblearn.over_sampling(下采样,under) import SMOTE
SMOTE.fit_sample(只对训练集操作)
误杀率比下采样低,当然recall也要低一点。
10.决策树:
衡量标准:熵值
表示随机变量的不确定性的度量
H(x)=-sum(p×logp)越大概率的得到的熵值越小,反之越大
决策一个节点的选择:
信息增益:表示特正X使得Y的不确定性减小的程度
遍历每个特征使得分类的熵值降低,减小不确定性
将使不确定性减少最多的特征为根节点,其他依次按照此排序
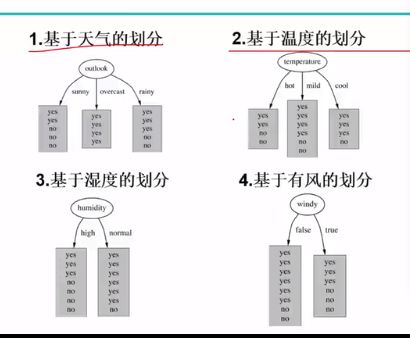
构造决策树:计算拿哪个特征值作为根结点比较合适
e.g. 9天打球,5天不打 此时的熵为9/14×log29/14+。。。。=0.940
基于不同特征时计算不同结果的熵值“:
以天气为根节点:
晴天:2天yes,3天NO,所以熵值为2/5乘以log2/5+...0.971
雨天: 0.971
对于没种天气的概率,雨天4/14,晴天5/14
总的熵值就等于:该天气概率乘以熵值+。。。=该特征的熵值《0.940
所以增益了
然后把其他特征也以这种方式计算增益,然后,找到最大增益的为根节点,
ID3算法:就是基于增益的算法
(假设拿ID作为特征 每个叶子节点熵值都为0 信息增益最大 但是ID只是一个编号对结果没有任何影响,但是其熵值争议增益最大,会把他作为最优特征,但这是不符合现实的
C4.5:ID3算法升级 信息增益率
考虑自身熵 对于ID本身【1,2,3,4,5,6,7】自身熵值是很大的
信息增益率就等于=信息增益/自身熵值 就可以避免上面ID的那种情况
CART:用GINI系数来做衡量标准 和熵值类似衡量标准类似,只是计算方式不同
计算公式:SUM(Pk(1-Pk))=1-SUM(Pk的平方)
连续值怎么办?就是说针对某一个特征时并没有很明确的子类,即像天气可以由晴天和雨天,但是没有这一些明确的分类时,而是一堆连续的数字,那么该如何求解其增益等等,就可以二分。找一个数作文二分的标准,然后小于他的作为一个属性来看待,大于他的又是一个,这样既可求解增益值。
连续值离散化 二分 找一个点按这个点来进行切分
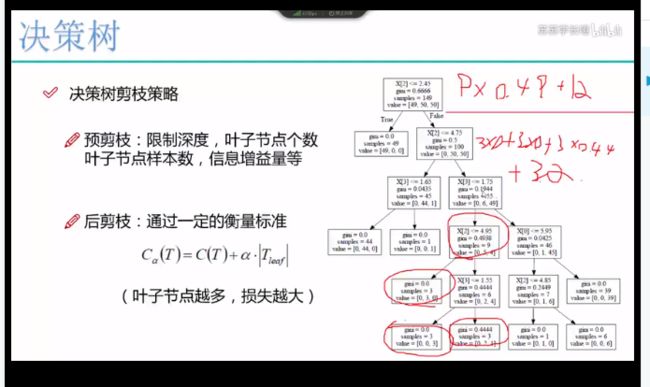
11.决策树剪枝策略:
决策树过拟合风险比较大,在测试集上效果不如在训练集上。
预剪枝:边建立决策树边进行剪枝 控制树的深度,叶子结点个数
限制广度
限制深度:限制特征 限制叶子结点个数
限制叶子节点样本数
后剪枝:Cα(T)=C(T)+α乘Tleaf的绝对值
Ct表示当前的一个损失,对每一个叶节点点,叶子节点样本数乘熵值或者基尼系数 把所有叶子节点损失加在一起
α表示限制叶子结点个数
叶子结点越多损失越大
12.sklearn实现
tree.DecisoinTreeRegressor(max_depth=1).fit()
参数:
1.criterion gini or entropy 选择熵或者基尼系数
2.splitter best or random 特征比较大的时候,从头到尾选择特征耗时间,best遍历所有,random选择其中一部分,默认best
3.max_features None
常用:4.max_depth最大深度,只选择最好的两个特征
常用:5.min——samples——split 叶子结点的样本数小于规定值则不要再份了
6.min_samples_laef限制了叶子节点最少的样本数 如果某叶子结点样本数目小于该值则回合兄弟节点一起被剪纸,如果样本量不大。则不需要管,如果10W则可尝试5
7.max_leaf_nodes通过限制最大的叶子节点数防止过拟合
12.决策树可视化
生成一个.dot文件:
dot_data=
tree.export_graphviz(
dtr(树的实例),
out_file=None,
feature_names=housing.feature_names[6:8]
filler=True
impurity=False,
rounded=True
)###生成一个.dot文件
展示一个.dot文件:
import pydotplus
graph=pydotplus.graph_from_dot_data(dot_data)
graph.get_nodes()[7].set_fillcolor("颜色")
from IPython.diplay import Image
Image(graph.create_png())
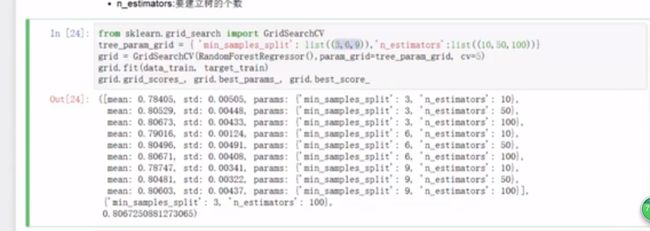
13.参数选择,用gridsearch来选择
sklearn.grid_search import GridSearchCV###也是通过交叉验证的
参数:(算法传进去,参数(用字典的格式),cv=5(进行几次的交叉验证 把训练集平均分开n份,A+B建模,C测试 最后吧每次结果取个平均)
grid.fit(_)
grid.grid_scores_,grid.best_params_,grid.best_score_
13.集成算法
Bagging:训练多个分类器取平均 f(x)=1/M SUM(Fm(x))
并行训练13.
e.g
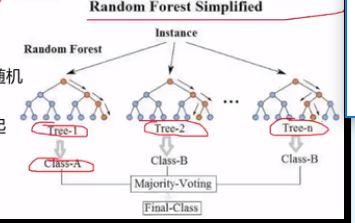
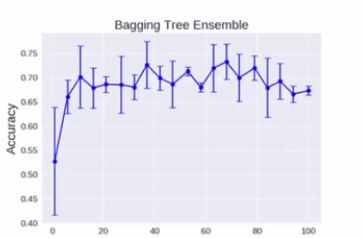
随机森林 随机:不同的树之间是有差异的,不是一模一样的。不是数越多越好。到一定程度就上下浮动了。
数据采样随机(有放回,随机),特征选择随机(随机选择N个)
优势:
不用特征选 择方案,可以处理高维度问题
A B C D 想要知道B特征的重要性 刚开始利用ABCD来训练。得到一个错误率,然后破坏B的数据构造B1,然后继续用AB1CD来训练得到第二个错误,比较这两个错误
A+B+C+D=====error1
A+B1+C+D====error2
error1约等于error2 B不重要 对结果影响不大
2>>>1远大于1 说明B的作用很大
Boosting模型:从弱学习器开始加强,通过加权来进行训练
A预测 有误差50 B树去预测残差 30 C树预测18 最终还有误差2
串行算法
典型代表:
AdaBoost,Xgboost
AdaBoost会根据前一次的分类效果调整数据权重
如果某一个数据在这次分错了,那么下一次就给他更大的权重
刚开始给每个测试数据一个权重
根据测试结果,对错的将其权重增加,当然
其他权重降低之后也可能会预测错,每次修改权重
权重越大,切分时越朝着它,
最终结果:每个分类器根据自身准确性来确定各自的权重,再合体分类越好权值越重
Stacking:
堆叠:堆叠各种各样的算法
第一阶段将特征输入得到结果值,可以选择任意多的分类器
第二阶段将第一阶段的输出作为输入,输出其结果
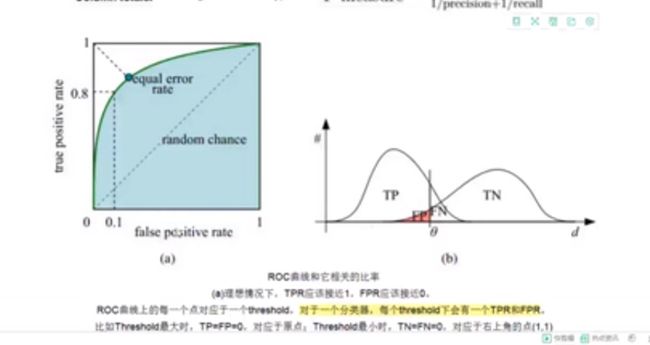
ROC和AUC明天在进行记录。