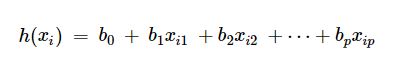【机器学习实战】线性回归

目录：

一、介绍

1.线性回归的类型

2.假设条件

二、用Python构建一个回归器步骤

三、用Python实现简单线性回归

1.模拟数据及绘图

2.简单线性回归过程

3.使用scikit-learn中的线性回归

四、用Python实现多元线性回归

1.加载Boston住房数据集数据

2.数据集分为训练集和测试集

3.计算出系数与截距

4.绘制散点图

五、应用领域

---

一、介绍

线性回归可以定义为统计模型，用于分析因变量与给定的一组自变量之间的线性关系。变量之间的线性关系意味着，当一个或多个自变量的值更改（增加或减少）时，因变量的值也将相应更改（增加或减少）。

数学上的关系可以借助以下方程式来表示：

Y = aX + b

在这里，Y是我们试图预测的因变量，X是我们用来进行预测的自变量，a是回归线的斜率，b是一个常数，称为截距。

1.线性回归的类型

• 简单线性回归
• 多元线性回归

2.假设条件

以下是关于由线性回归模型建立的数据集的一些假设：

多重共线性：线性回归模型假设数据中很少或没有多重共线性。基本上，当自变量或要素具有相关性时，就会发生多重共线性。

自相关：数据中几乎没有自相关。基本上，当残差之间存在依赖性时，就会发生自相关。

变量之间的关系：线性回归模型假定响应变量和特征变量之间的关系必须是线性的。

二、用Python构建一个回归器步骤

Scikit-learn，一个用于机器学习的Python库，也可以用于在Python中建立一个回归器。

在以下示例中，我们将构建基本的回归模型，该模型将使一条线适合数据，即线性回归。在Python中构建回归器的必要步骤如下：

步骤1：导入必要的python包。

步骤2：导入数据集。

步骤3：将数据整理到训练和测试集中。

步骤4：模型构建和预测。

第5步：绘图和可视化。

步骤6：性能计算。性能指标包括：均方误差MSE、均方根误差RMSE、平均绝对误差MAE与R Squared等。

三、用Python实现简单线性回归

1.模拟数据及绘图

# 导包
import numpy as np
import matplotlib.pyplot as plt

# 模拟数据
x = np.array([1., 2., 3., 4., 5.])
y = np.array([1., 3., 2., 3., 5.])

# 绘制散点图
plt.scatter(x, y)
plt.axis([0, 6, 0, 6]) # 设置x，y轴的氛围
plt.show()

2.简单线性回归过程

①计算回归线斜率和截距

斜率和截距公式如下（注：本案例斜率为a，截距为b）：

# 求x，y的平均值
x_mean = np.mean(x)
y_mean = np.mean(y)

# 求斜率a和截距b
num = 0.0
d = 0.0
for x_i, y_i in zip(x, y):
    num += (x_i - x_mean) * (y_i - y_mean)
    d += (x_i - x_mean) ** 2

a = num / d
b = y_mean - a * x_mean

print(a)
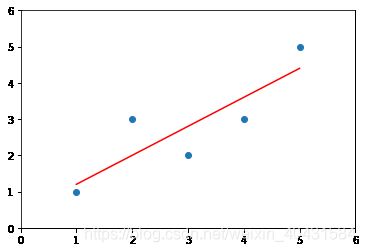
print(b)

0.8

0.39999999999999947

②绘制带回归线的散点图

# 回归线
y_hat = a * x + b

# 绘制带回归线的散点图
plt.scatter(x, y)
plt.plot(x, y_hat, color = 'r')
plt.axis([0, 6, 0, 6])
plt.show()

③预测数据

x_predict = 6
y_predict = a * x_predict + b
print(y_predict)

5.2

3.使用scikit-learn中的线性回归

# 导包
from sklearn.linear_model import LinearRegression
import numpy as np

# 创建线性回归对象
reg = LinearRegression()

# 模拟数据 
x = np.array([1., 2., 3., 4., 5.])
x_train = x.reshape(-1,1)
y_train = np.array([1., 3., 2., 3., 5.])

# 训练
reg.fit(X_train,y_train)


# 计算出的斜率与截距
print(reg.coef_)    
print(reg.intercept_)  

array([0.8])

0.39999999999999947

# 预测数据
y_predict = reg.predict(x_train)

# 绘图
plt.scatter(x_train, y_train)
plt.plot(x, y_predict, color = 'r')
plt.axis([0, 6, 0, 6])
plt.show()

很显然，结果与之前预测的基本一致。

四、用Python实现多元线性回归

简单线性回归的扩展使用两个或多个特征预测响应。数学上，我们可以解释如下：

考虑具有n个观测值，p个特征（即自变量）和y作为一个响应（即因变量）的数据集，p个特征的回归线可以如下计算：

1.加载Boston住房数据集数据

# 导包
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

# 加载boston数据
boston = datasets.load_boston()

# 定义特征矩阵X和响应向量y
X = boston.data
y = boston.target

# 过滤掉y=50的数据，因为y溢出的数据都为50，考虑后续数据预测的准确性，删除
X = X[y < 50.0]
y = y[y < 50.0]

X.shape    # 显示为(490, 13)

2.数据集分为训练集和测试集

from model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, seed = 666)  # seed为随机种子

3.计算出系数与截距

from sklearn.linear_model import LinearRegression

# 创建线性回归对象并训练模型
reg = LinearRegression()
reg.fit(X_train, y_train)

# 计算出的系数与截距
print(reg.coef_)    
print(reg.intercept_)  

array([-1.20354261e-01,  3.64423279e-02, -3.61493155e-02,  5.12978140e-02,
       -1.15775825e+01,  3.42740062e+00, -2.32311760e-02, -1.19487594e+00,
        2.60101728e-01, -1.40219119e-02, -8.35430488e-01,  7.80472852e-03,
       -3.80923751e-01])

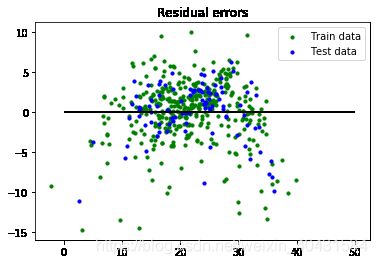
34.11739972320428

4.绘制散点图

plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train, color = "green", s = 10, label = 'Train data')
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test, color = "blue", s = 10, label = 'Test data')
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
plt.legend(loc = 'upper right')
plt.title("Residual errors")  # 残差
plt.show()

五、应用领域

ML回归算法的应用如下：

1.预测或预测分析 

回归的重要用途之一是预测或预测分析。例如，我们可以预测GDP，石油价格或简单地说随着时间的推移而变化的定量数据。

2.优化 

我们可以借助回归优化业务流程。例如，商店经理可以创建统计模型以了解顾客来访的时间。

3.错误纠正 

在业务中，做出正确的决定与优化业务流程同等重要。回归可以帮助我们做出正确的决定，也可以帮助我们纠正已经实施的决定。

4.经济学 

这是经济学中最常用的工具。我们可以使用回归来预测供应，需求，消耗，库存投资等。

5.财务 

金融公司始终对最小化风险投资组合感兴趣，并希望了解影响客户的因素。所有这些都可以借助回归模型进行预测。