TGRS2020/遥感：Multisource Domain Adaptation for Remote Sensing Using Deep Neural Netw基于深度神经网络的遥感多源域自适应

0.摘要

在将机器学习应用于遥感问题时，通常会出现多个训练数据源(称为域)可用于同一任务的情况。每个领域训练单独的模型是低效的，这促使从多个来源学习单个模型。例如，局部气候区(LCZ)分类问题旨在从城市和农村环境的遥感图像产生表面结构的逐像素分类。这些分类地图需要在不同的时间为不同的城市生成。为了有效地做到这一点，必须根据手头的任务调整来自不同来源(即城市)的可用训练数据。然而，多源域适应(MDA)是一个具有挑战性的问题，特别是当这些源之间的数据分布发生重大变化时。在本文中，我们提出了一个可扩展但简单的自适应MDA (AMDA)框架来解决这个问题。AMDA还能够比现有基线更有效地处理不同来源之间不平衡的数据分布。我们还将最初为域扩展(DE)提出的两种技术扩展到DA任务。将AMDA和扩展的DE技术应用于LCZ分类问题。尽管AMDA很简单，但它能够比基线提高12%以上

1.概述

在过去的十年里，机器学习(ML)已经成功地应用于解决具有挑战性和复杂的任务。这种成功的主要原因之一是大量注释数据的可用性。为了获得最佳结果，注释数据必须是高质量和高数量的。但是，为新任务获取带注释的数据是昂贵和耗时的。因此，需要利用以前解决过的问题所获得的知识来解决当前的任务，这就是迁移学习[1]。
领域适应(DA)是一种流行的迁移学习技术，系统的目标是将从一个领域(称为源领域)学习到的知识适应到另一个相关领域(称为目标领域)。DA问题的主要挑战是源数据和目标数据分布之间存在显著变化;因此，使用源数据进行训练的传统监督模型在目标域上更容易失败。对于分类任务，最具挑战性的数据处理问题之一是无监督数据处理，即目标域数据不存在注释。新兴应用程序通常遵循UDA设置，这要求利用其他相关领域的注释数据。
多源数据分析(MDA)是数据分析的另一种形式，它意味着存在多个源域。MDA问题与遥感应用密切相关。例如，美国国家航空航天局(NASA)和美国地质调查局(USGS)于2013年发射的多光谱仪器陆地卫星8号(Landsat 8)，它每16天绕地球一周。每个场景面积约33 000平方公里，地面分辨率为30米(可见、近红外、SWIR);100(热);15m(全色)。Landsat 8场景是公开的GeoTiff压缩文件(文件大小≈1gb)[2]。每天大约获得500幅图像。为了及时地利用和受益于这一巨大的数据量，标签过程必须最小化或消除。然而，地球的大气条件和季节变化导致不同场景之间的数据有很大的变化。因此，在这个数据集中，每个场景都可以看作是一个独立的领域，需要应用DA对看不见的数据(目标)获得高质量的结果。
深度神经网络(DNNs)已经将包括遥感在内的不同领域的许多基准的最新水平提高到了一个新的水平[3]。由于其卓越的性能，处理大规模数据的能力，以及提取鲁棒和丰富的可转移表示[4]的能力，DNN技术被认为是解决迁移学习挑战的最佳候选技术之一。特别是卷积神经网络(CNNs)，被认为是可视化应用[5]的最先进的方法。
将CNNs应用于基于遥感图像的分类任务，如场景检测，其目标是将整个图像分类为几个定义的类别之一的任务是简单的[6]。然而，大多数遥感图像分类任务通常是基于像元的任务，这意味着输入是与某个像元相关的光谱特征。为了利用cnn完成这项任务，必须将问题从纯粹的基于像素的预测转化为基于图像的(即基于补丁的)[7]输入。
在本文中，我们提出了一个简单的对大规模MDA有效的端到端框架。我们还设计并实现了不同的基于cnn的MDA技术来解决遥感分类问题。特别是，我们针对最近发展的局部气候带(LCZ)[8]分类问题。LCZ映射模式提供了城市和农村景观的通用分类地图。该模式由17类组成，反映了影响气温的结构和土地覆盖属性。目前，世界城市数据库和门户工具(WUDPT)[9]使用众包方式收集世界各地城市的人口普查，LCZ框架已被选择作为映射模式，以一致的方式表征城市。为了开发这些LCZ地图，WUDPT过程使用监督ML技术来获得每个城市的完整LCZ地图。然而，该系统完全依赖于非专业用户来标记每个特定城市的训练样本，并且必须执行一个验证过程来评估每个地图的质量
我们在MDA上的工作被建议作为一个更高效和更精确的LCZ制图系统的候选工具。提出的技术旨在减少生成这些地图所需的时间，并减少众包带来的不确定性。本文的主要贡献可以总结如下。
1） 该框架是一种新型的端到端自适应MDA（AMDA）技术，简单、健壮，能够处理不平衡的大规模MDA问题。
2） 我们还扩展了最近引入的两种MDA域扩展（DE）算法。
3） 最后，我们在大规模公共遥感基准：LCZ（local climate zone）分类问题上实现并实证评估了所提出的技术。

2.方法

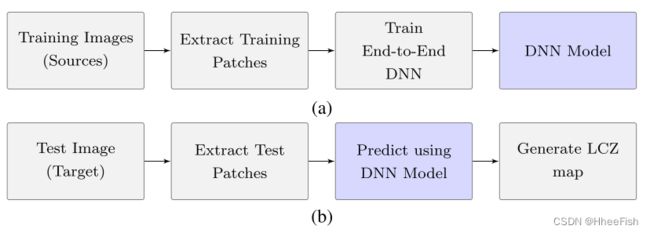
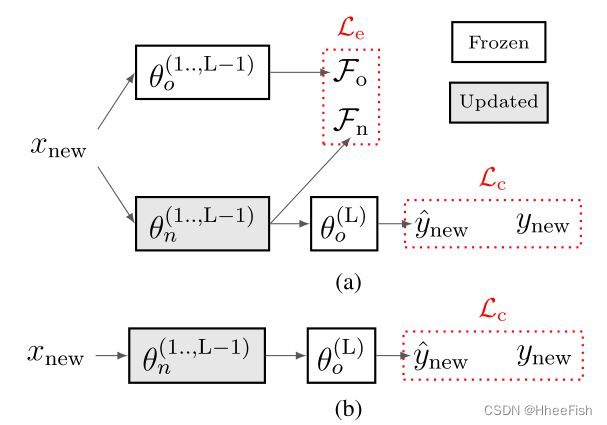
图1所示。提出了LCZs映射的MDA框架。(a)训练阶段。(b)部署阶段

2.1.基于像素到基于面片的预测

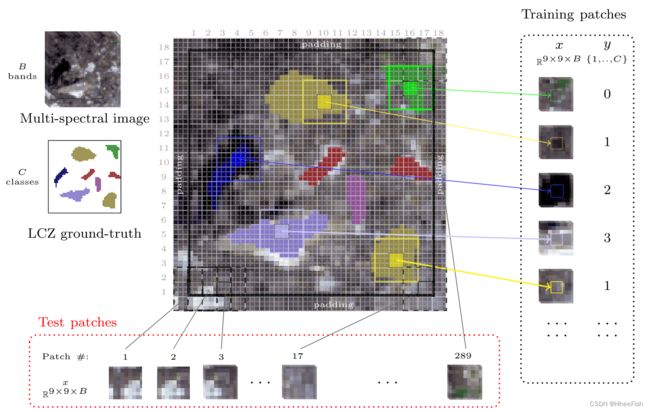
图2所示。补丁生成过程。图像大小为51 × 51, w = 3 × 3, s = 3, p = 9 × 9。图像用反射填充，以便提取接近图像边界的补丁。使用此设置，滑动窗口不会重叠，但补丁会重叠，如图所示。从一幅图像中可以提取的patch总数为(图像大小)/(w × w)，本例中可以提取出289个patch。为了说明问题，我们只展示了提取的训练补丁中的5个样本。

从给定遥感图像中提取斑块的过程如图2所示。给定具有B波段的图像，使用大小为w的滑动窗口扫描整个图像。在扫描过程中，使用步长标量s对滑动窗口进行步长（例如，移动）。提取以所有扫描滑动窗口为中心的大小为（p×p）的面片。设置w=（1，1）和s=1将导致从图像中提取所有可能的面片。为了提高效率，应考虑w>1、s>1和p>s+w，这将导致提取样本中的更多多样性，并且还将显著减少训练和测试的处理需求。
生成训练面片时，滑动窗口充当过滤器，仅考虑具有与地面真值图重合的滑动窗口的面片（见图2）。另一方面，地面真值图不适用于测试图像；因此，将处理所有提取的面片。然而，单个测试补丁的结果将填充到该补丁的滑动窗口中。

2.2.架构

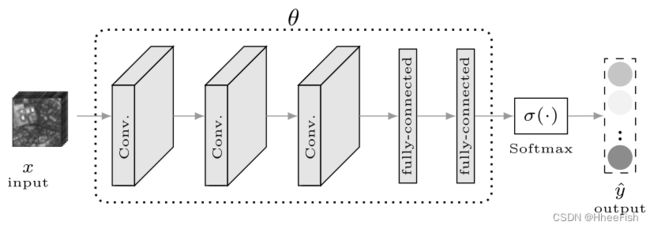
图3所示。我们的基线CNN架构。

接下来，我们描述了拟议的DA网络，该网络可以使用从源图像中提取的面片进行训练。然后使用这些网络进行预测，当更多训练源可用时，可能会对其进行重新训练或微调。这些网络的一个重要属性是对源域的数量没有限制，并且网络的大小或复杂性不会受到域数量的影响。此外，这些网络使用公共组件，因此易于使用任何深度学习库（如PyTorch[47]或TensorFlow[48]）实现。我们在这里考虑的基线网络是CNN，如图3所示。该网络由多个卷积块和完全连接的层组成。网络的输出向量是最后一个完全连接层的softmax。优化网络参数θ，以最小化相对于网络参数θ的分类损失L_y(θ)。网络的优化参数（θˆ）可以用下式估计

分类损失L_y使用以下表达式给出的经典交叉熵计算：

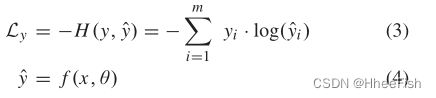
其中，y和yˆ分别是地面真值和网络输出的独热编码向量，f是由θ参数化的函数，该函数将输入x映射到输出yˆ。输出向量的大小为m，是任务中的类标签数。该损失是使用从训练数据中采样的（x，y）对的小批量来计算的。通过对最后一个完全连接的层输出向量（z）应用softmax来计算网络输出

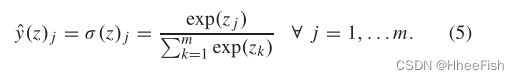
使用随机梯度下降（SGD）更新网络参数（θ），如下所示：

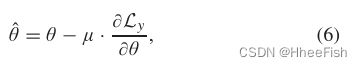
其中μ是学习率，以及(∂Ly）/(∂θ）是Ly对网络参数θ的偏导数。
所有提出的方法都遵循相同的目标，都使用SGD更新网络参数。与前面讨论的分布匹配方法类似，我们还向网络目标中添加了DA损耗项。使用相同的符号，我们对基线网络使用DA网络目标，表示为

其中λ_y和λ_DA分别是分类损失和DA损失影响的控制参数。虽然所有提出的方法都使用（7），但它们在计算L_DA项的方式上有所不同。然而，分类损失（L_y）在所有方法中是相同的，并根据（3）计算
在本文中，我们研究了几种训练该网络的方法，包括PNN和DANN。然而，由于篇幅的限制，我们将只讨论最有前途的技术。

2.3.通过知识扩展网络进行适应

在本节中，我们重点介绍了最近引入的两种DE算法，我们将其修改为用于DA。这些模型的共同主题是逐步更新网络参数，网络目标包括克服灾难性遗忘的术语。

2.3.1.LwF

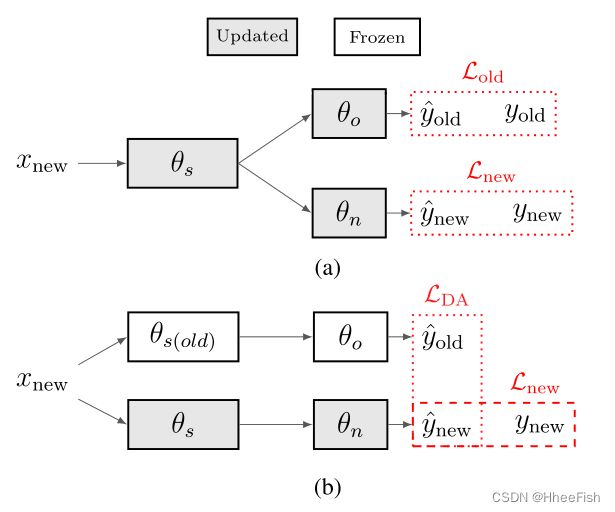
图4所示。LwF。(a) LwF域扩展目标。(b) LwF修正- DA目标。

LwF[35]被提出用于DE，以避免灾难性遗忘，并生成一个统一的模型，该模型在两个任务中都表现良好。在典型的DE设置中，旧的任务训练数据不可用；然而，使用旧任务数据学习的预训练网络是可用的。这是DE旨在扩展的网络。
图4（a）说明了LwF如何实现这一点。在旧任务（启动网络）θ_o上训练的网络分为共享表示学习层（θ_s）和任务特定层（θ_o）。LwF通过为新任务（θ_n）创建新层来扩展该网络。首先，使用新数据x_new，旧任务响应记录如下：

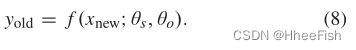
需要注意的是，记录的y_old值并不代表旧任务的清晰标签，而是基于新任务数据的任务标签的后验概率。然而，它将被视为实际的旧任务地面真相，并且从未更新。然后，y_old将可用的新任务训练数据对（x_new，y_new）添加到一个新的训练集，D={x_new，（y_new，y_old）}。
随机初始化新层θ_n，并优化整个网络参数（θ_s、θ_o、θ_n），以联合最小化相对于新任务地面实况（y_new）的损失和相对于记录地面实况（y_old）的损失，其可以表示为

其中，L_old是旧任务损失，L_new是新任务损失，λ_old是控制旧任务损失影响的超参数。（3）中的交叉熵损失用于计算这两种损失。
在本文中，我们采用了LwF用于MDA的相同策略，如图4（b）所示。因为所有域的标签空间都是相同的，所以θ_n和θ_o在大小和架构方面是相同的。此外，由于我们将在多个域上优化网络，我们需要有效地计算旧网络对新域数据的响应。我们没有在每次更改输入数据时重新计算和记录y_old，而是为旧网络的参数（θ_s(old)，θ_o）创建一个单独的分支，并冻结它们，同时使用新的域数据优化新网络参数（θ_s，θ_n）。这使我们能够动态地重新计算y_old，并且每当我们迭代到不同的域时，不需要更新它并为整个域数据记录它。此外，对于DA，我们希望旧网络和更新网络对给定输入保持相同的响应；因此，我们修改了L_old（L_DA用于替换L_old），以使更新的新网络输出与冻结的旧网络输出相同。因此，L_DA可以表示为

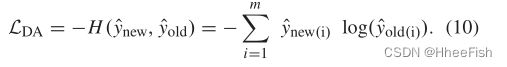
最后，我们进一步更改LwF训练协议，以重新迭代所有源域，我们将在后面讨论。

2.3.2.LFL

图5所示。LFL。(a) LFL域扩展(LFL- l2)。(b) LFL-Fix域适配。

与LwF不同，LFL[36]，如图5(a)所示，使用不同的目标来避免灾难性遗忘。首先，在应用softmax函数之前冻结最后一层隐含层(θ^(L)_o)，以确保固定分类器的决策边界(我们将在本文剩余部分将网络的最后一层称为logits层)。第二个目标涉及到鼓励旧网络的提取特征(F_o)与新网络的提取特征(F_n)相似。使用上述表示法，F_n计算如下:

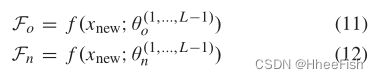
其中f是θ^{(1，…，L−1)}_o参数化的映射函数，它将输入x映射到L−1层的隐藏表示。用L2范数计算F_o和F_n之间的相似度如下:

与LwF相似，采用启动网络进行扩展，对θ^{(1，…，L−1)}_o进行优化，使

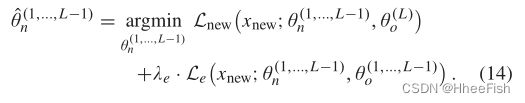
与LwF不同的是，通过修复最后一层，LFL限制了两个任务的类数量相同。此外，用于评估LFL[36]的DE场景可以被视为DA问题。因此DA采用LFL，不做任何修改，在我们(7)的DA目标中用L_e(13)代替L_DA。
虽然Le将两个任务的提取特征归纳为相似的，但我们认为当logits层θ (L)o是固定的时候，这个目标是隐含的。固定θ (L)o会使网络在优化新域时服从给定的决策边界，从而促使新网络产生与旧网络相似的特征。因此，我们也研究了丢弃DA损失(例如，L_DA = 0)和仅仅固定logits层的影响，如图5(b)所示。我们将这种方法称为LFL-Fix，将具有显式DA损失(如L_DA = L_e)的方法称为LFL-L2。
由于LwF和LFL算法在DA中都进行了改进，因此采用了迭代训练方法。算法1显示了给定源域数据的基本训练周期。在每个训练周期中，只有一个源被用于如上所述的更新网络。在这个周期中，通过从提供的源数据(S)中随机抽样一个小批来执行k次SGD更新。

当修改DA的LwF和LFL时，我们遇到的主要挑战是用于检测网络中所有源的改进的控制信号(或指示器)的类型。我们研究了几个分数(指标)作为控制信号，基于一个暂停验证集，如平均损失，最大损失，平均精度和最小精度。在这些得分中，我们发现最大限度地提高源内的最小精度可以提供最稳定和准确的控制信号。假设第i个源的验证精度是a_i，那么其中的验证分数φ可以按如下方式计算:

屏蔽验证集从所有训练源中提取，从不用于训练。为了最大限度地提高算法的训练速度，该验证集的大小应该相对较小。(例如，源训练数据的5%-10%)。该算法还假定启动网络(θ_o)的可用性，在单一源上预训练。在每个训练周期结束时，使用验证集对网络进行评估(算法1中的步骤2)，并根据(15)计算验证分数。如果检测到改进，则用当前网络参数更新旧的网络参数，并保存该网络，认为该网络是优化最好的网络。最后，如果在连续预定义的训练周期内没有报告验证分数的增强，算法将终止。需要注意的是，LwF和LFL-L2都使用了算法1;然而，LFL-Fix在适应过程中不需要保持原有的网络参数θ_o，而且logits层θ^(L)_n是冻结的，从不更新

2.4.AMDA

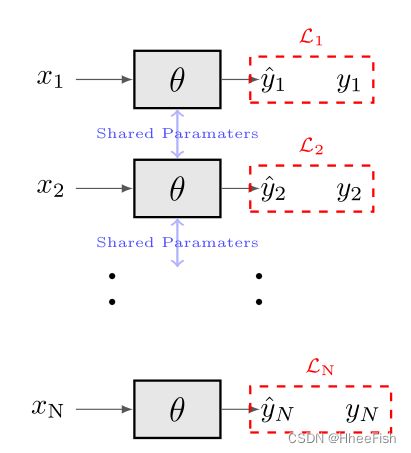
图6所示。AMDA网络架构用于N个域(x₁, x₂，…x_N)

在处理DA时，重要的是要记住:1)来自所有源域的数据在适配过程中都是可用的，2)任务在所有域中都是相同的。这些主要特征促使我们开发AMDA，我们设计了一个简单的端到端MDA算法。AMDA网络如图6所示，由N个支路组成，其中N为信号源数量，所有支路共享相同的参数。每个分支的损失是使用规则交叉熵计算，如(3);但是，整个网络的损耗是这N个损耗的加权和，如下所示:

式中，λ_i为第i支的损失权重。利用验证集上的网络性能计算λ_i，如下所示:

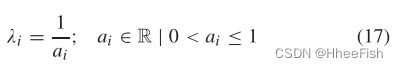
其中a_i为第i个源的验证精度。(17)式为性能较低的分支设置了较高的权重，因此从这些分支得到的梯度会相应放大。另一方面，性能优越的分支机构的损失不会被放大。因此，性能较低的分支对更新的网络参数影响较大。
AMDA的训练协议如算法2所示。

对所有分支统一初始化损失权值，并将损失权值设置为(1)/(N)(步骤1)。与修改后的LwF和LFL算法类似，实际训练在步骤5中进行，其中SGD的k步执行，每个SGD步骤使用从所有源采样的小批量优化网络参数。在这k次SGD更新期间，损失权值是固定的，在这些更新之后，使用所有源的验证集对网络进行评估。在步骤6中，根据(15)和(17)分别计算验证评分和损失权值。如果检测到改进(步骤8)，则保存当前网络参数，并认为是迄今为止最好的网络(步骤10)。只要源域的验证分数有所提高，就会重复这个训练过程。当在预定义的连续迭代次数中没有报告改进时，算法终止。
AMDA算法与之前提出的算法的主要区别在于它的实现简单和它的参数数量少，因为它们在所有分支之间共享。此外，这也完全符合Mansour等人[13]的观点，即基于源分布加权组合的模型比基于均匀源组合的模型更好。基于此观察，基线网络被认为类似于AMDA，但使用了一个统一的源组合(例如，所有源的损失权值固定为λ_i = (1)/(N)))。

参考文献

[1] S. J. Pan and Q. Yang, “A survey on transfer learning,” IEEE Trans.
Knowl. Data Eng., vol. 22, no. 10, pp. 1345–1359, Oct. 2010.
[ 2 ] D . P . R o y et al., “Landsat-8: Science and product vision for terrestrial global change research,” Remote Sens. Environ., vol. 145, pp. 154–172, Apr. 2014.
[ 3 ] X . X . Z h u et al., “Deep learning in remote sensing: A comprehensive review and list of resources,” IEEE Geosci. Remote Sens. Mag., v o l . 5 , no. 4, pp. 8–36, Dec. 2017.
[4] J. Donahue et al., “DeCAF: A deep convolutional activation feature for generic visual recognition,” in Proc. ICML, vol. 32, 2014, pp. 647–655.
[5] G. Csurka, “A comprehensive survey on domain adaptation for visual applications,” in Domain Adaptation in Computer Vision Applications.
Cham, Switzerland: Springer, 2017, pp. 1–35.
[6] A. Romero, C. Gatta, and G. Camps-V alls, “Unsupervised deep feature extraction for remote sensing image classification,” IEEE Trans. Geosci.
Remote Sens., vol. 54, no. 3, pp. 1349–1362, Mar. 2016.
[7] A. Sharma, X. Liu, X. Y ang, and D. Shi, “A patch-based convolutional neural network for remote sensing image classification,” Neural Netw., vol. 95, pp. 19–28, Nov. 2017.
[8] I. D. Stewart and T. R. Oke, “Local climate zones for urban temperature studies,” Bull. Amer. Meteorol. Soc., vol. 93, no. 12, pp. 1879–1900, Dec. 2012.
[9] G. Mills, J. Ching, L. See, B. Bechtel, and M. Foley, “An introduction to the WUDAPT project,” in Proc. 9th Int. Conf. Urban Climate, Toulouse, France, 2015, pp. 20–24.
[10] N. Japkowicz and S. Stephen, “The class imbalance problem: A systematic study,” Intell. Data Anal., vol. 6, no. 5, pp. 429–449, Oct. 2002.
[11] S. Chang, W. Han, J. Tang, G.-J. Qi, C. C. Aggarwal, and T. S. Huang, “Heterogeneous network embedding via deep architectures,” in Proc.
21st ACM SIGKDD Int. Conf. Knowl. Discovery Data Mining, 2015, pp. 119–128.
[12] J. Blitzer, K. Crammer, A. Kulesza, F. Pereira, and J. Wortman, “Learning bounds for domain adaptation,” in Proc. NIPS, 2008, pp. 129–136.
[13] Y . Mansour, M. Mohri, and A. Rostamizadeh, “Domain adaptation with multiple sources,” in Proc. NIPS, 2009, pp. 1041–1048. [14] S. Ben-David, J. Blitzer, K. Crammer, A. Kulesza, F. Pereira, and J. W. V aughan, “A theory of learning from different domains,” Mach.
Learn., vol. 79, nos. 1–2, pp. 151–175, May 2010.
[15] S. Sun, H. Shi, and Y . Wu, “A survey of multi-source domain adaptation,” Inf. Fusion, vol. 24, pp. 84–92, Jul. 2015.
[16] J. Y osinski, J. Clune, Y . Bengio, and H. Lipson, “How transferable are features in deep neural networks?” in Proc. NIPS, 2014, pp. 3320–3328.
[17] G. E. Hinton and R. R. Salakhutdinov, “Reducing the dimensionality of data with neural networks,” Science, vol. 313, no. 5786, pp. 504–507, 2006.
[18] Y . Bengio, P. Lamblin, D. Popovici, and H. Larochelle, “Greedy layerwise training of deep networks,” in Proc. NIPS, 2007, pp. 153–160.
[19] X. Glorot, A. Bordes, and Y . Bengio, “Domain adaptation for largescale sentiment classification: A deep learning approach,” in Proc. ICML, 2011, pp. 513–520.
[20] P. Vincent, H. Larochelle, Y . Bengio, and P.-A. Manzagol, “Extracting and composing robust features with denoising autoencoders,” in Proc.
25th Int. Conf. Mach. Learn., 2008, pp. 1096–1103.
[21] M. Ghifary, W. B. Kleijn, M. Zhang, D. Balduzzi, and W. Li, “Deep reconstruction-classification networks for unsupervised domain adaptation,” in Proc. Eur. Conf. Comput. Vis. Springer, 2016, pp. 597–613.
[22] K. Bousmalis, G. Trigeorgis, N. Silberman, D. Krishnan, and D. Erhan, “Domain separation networks,” in Proc. NIPS, 2016, pp. 343–351.
[23] E. Tzeng, J. Hoffman, N. Zhang, K. Saenko, and T. Darrell, “Deep Domain Confusion: Maximizing for domain invariance,” 2014, arXiv:1412.3474. [Online]. Available: https://arxiv.org/abs/1412.3474 [24] K. M. Borgwardt, A. Gretton, M. J. Rasch, and H.-P. Kriegel, “Integrating structured biological data by kernel maximum mean discrepancy,” Bioinformatics, vol. 22, no. 14, pp. e49–e57, 2006.
[25] M. Long, Y . Cao, J. Wang, and M. I. Jordan, “Learning transferable features with deep adaptation networks,” in Proc. ICML, 2015, pp. 97–105.
[26] A. Gretton et al., “Optimal kernel choice for large-scale two-sample tests,” in Proc. NIPS, 2012, pp. 1205–1213.
[27] B. Sun and K. Saenko, “Deep CORAL: Correlation alignment for deep domain adaptation,” in Proc. ECCV Workshops, 2016, pp. 443–450.
[28] A. Rozantsev, M. Salzmann, and P. Fua, “Beyond sharing weights for deep domain adaptation,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 41, no. 4, pp. 801–814, Apr. 2019.
[29] M. Long, Y . Cao, J. Wang, and M. I. Jordan, “Deep transfer learning with joint adaptation networks,” in Proc. Int. Conf. Mach. Learn., vol. 70, 2017, pp. 2208–2217.
[30] Y . Ganin et al., “Domain-adversarial training of neural networks,” J. Mach. Learn. Res., vol. 17, no. 59, pp. 1–35, 2016.
[31] E. Tzeng, J. Hoffman, K. Saenko, and T. Darrell, “Adversarial discriminative domain adaptation,” in Proc. CVPR, Jul. 2017, pp. 7167–7176.
[32] I. J. Goodfellow, M. Mirza, D. Xiao, A. Courville, and Y . Bengio, “An empirical investigation of catastrophic forgetting in gradient-based neural networks,” 2013, arXiv:1312.6211. [Online]. Available: https:// arxiv.org/abs/1312.6211 [33] A. A. Rusu et al., “Progressive neural networks,” 2016, arXiv: 1606.04671. [Online]. Available: https://arxiv.org/abs/1606.04671 [34] J. Kirkpatrick et al., “Overcoming catastrophic forgetting in neural networks,” Proc. Nat. Acad. Sci. USA, vol. 114, no. 13, pp. 3521–3526, 2017.
[35] Z. Li and D. Hoiem, “Learning without forgetting,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 40, no. 12, pp. 2935–2947, Dec. 2018.
[36] H. Jung, J. Ju, M. Jung, and J. Kim, “Less-forgetful learning for domain expansion in deep neural networks,” in Proc. 32nd AAAI Conf. Artif.
Intell., 2018, pp. 1–8.
[37] R. Chattopadhyay, Q. Sun, W. Fan, I. Davidson, S. Panchanathan, and J. Ye, “Multisource domain adaptation and its application to early detection of fatigue,” ACM Trans. Knowl. Discovery Data, vol. 6, no. 4, p. 18, Dec. 2012.
[38] Q. Sun, R. Chattopadhyay, S. Panchanathan, and J. Y e, “A two-stage weighting framework for multi-source domain adaptation,” in Proc.
NIPS, 2011, pp. 505–513.
[39] H. Zhao, S. Zhang, G. Wu, J. M. Moura, J. P . Costeira, and G. J. Gordon, “Adversarial multiple source domain adaptation,” in Proc. NIPS, 2018, pp. 8559–8570.
[40] R. Xu, Z. Chen, W. Zuo, J. Y an, and L. Lin, “Deep cocktail network: Multi-source unsupervised domain adaptation with category shift,” in Proc. CVPR, Jun. 2018, pp. 3964–3973.
[41] J. Hoffman, M. Mohri, and N. Zhang, “Algorithms and theory for multiple-source adaptation,” in Proc. NIPS, 2018, pp. 8246–8256.
[42] B. Demir, F. Bovolo, and L. Bruzzone, “Updating land-cover maps by classification of image time series: A novel change-detection-driven transfer learning approach,” IEEE Trans. Geosci. Remote Sens., vol. 51, no. 1, pp. 300–312, Jan. 2013.
[43] L. Bruzzone and M. Marconcini, “Domain adaptation problems: A DASVM classification technique and a circular validation strategy,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 32, no. 5, pp. 770–787, May 2010.
[44] G. Matasci, M. V olpi, M. Kanevski, L. Bruzzone, and D. Tuia, “Semisupervised transfer component analysis for domain adaptation in remote sensing image classification,” IEEE Trans. Geosci. Remote Sens., vol. 53, no. 7, pp. 3550–3564, Jul. 2015.
[45] M. V olpi, G. Camps-Valls, and D. Tuia, “Spectral alignment of multitemporal cross-sensor images with automated kernel canonical correlation analysis,” J. Photogramm. Remote Sens., vol. 107, pp. 50–63, Sep. 2015.
[46] N. Y okoya et al., “Open data for global multimodal land use classification: Outcome of the 2017 IEEE GRSS data fusion contest,” IEEE J. Sel.
Topics Appl. Earth Observ. Remote Sens., vol. 11, no. 5, pp. 1363–1377, May 2018.
[47] A. Paszke et al., “Automatic differentiation in PyTorch,” in Proc. NIPS Autodiff Workshop, 2017.
[48] M. Abadi et al., “TensorFlow: A system for large-scale machine learning,” in Proc. OSDI, vol. 16, 2016, pp. 265–283.
[49] S. Foga et al., “Cloud detection algorithm comparison and validation for operational landsat data products,” Remote Sens. Environ., vol. 194, pp. 379–390, Jun. 2017.
[50] D. P. Kingma and J. L. Ba, “Adam: A method for stochastic optimization,” in Proc. Int. Conf. Learn. Represent., 2015, pp. 1–15.