论文翻译 —— Model Free Episodic Control

• 标题：Model Free Episodic Control
• 文章链接：Model Free Episodic Control
• 代码实现：sudeepraja Model-Free-Episodic-Control
• 领域：强化学习 - 情节控制（episodic control）
• 注：方括号为原文中参考文献引用，具体引用文章请下载原文查看

---

免模型情节控制

• 摘要：SOAT深度强化学习算法需要数百万次交互才能达到人类水平的表现，另一方面，人类则可以在第一次探索时就迅速发现并利用环境中高回报的细微差异。通常认为这种快速学习的能力来自于大脑中的海马体及其情节记忆能力（capacity for episodic memory）。 本文中，我们研究了一个简单的海马情节控制模型（model of hippocampal episodic control）能否学习解决困难的顺序决策任务。 我们证明，它不仅比SOAT深度强化学习算法更快地学到了高回报的策略，而且在一些更具挑战性的领域中获得了更高的整体回报（overall reward）。

1. Introduction

• 深度强化学习最近在各种领域取得了显着的成功 [23, 32]。但它的样本效率非常低。例如，在 Atari 游戏领域 [2]，深度强化学习 (RL) 系统通常需要与游戏模拟器进行数千万次交互，花费数百小时的游戏时间，才能达到人类水平的表现。正如 [13] 所指出的，人类学会玩这些游戏的速度要快得多。本文解决的问题就是如何在没有任何特定领域先验知识（domain-specific prior knowledge）的情况下在机器上模拟这种快速学习能力。
• 当前的深度RL算法可能会发生或者被显示在高奖励的动作序列上。不幸的是，由于底层策略或价值函数的梯度更新（gradient-based updates）很缓慢，这些算法需要大量的步骤来吸收（assimilate）这些信息并将其转化为策略性能的提升。 因此，这些算法缺乏快速锁定成功策略的能力。文献 [16] 引入的 Episodic control 是一种补偿方法，它可以快速重现观察到的成功策略。Episodic control 记录了高回报的经验，它学到的策略要试图重现这些曾得到过高回报的动作序列。
• 在大脑中，这种非常快速的学习形式得到了海马体和相关内侧颞叶结构的强力佐证 [1, 34]。 例如，在一个老鼠寻找隐藏平台的任务中，这些结构的损伤会影响老鼠的表现 [24, 36]。 海马学习被认为是基于经验实例的（instance-based） [18, 35]，这与皮质系统形成鲜明对比，后者学习的是输入分布的广义统计结论[20, 27, 41]。海马系统可能会把环境状态和从各种可能的动作获得的回报共同编码表示（co-representing），以此指导顺序决策。这样编码后，对于给定的探测状态（probe state），每个可能动作的收益可以通过 CA3子区域（译注：这是海马体上的一个区域）中的模式补全（pattern completion）来获取 [9, 21, 26, 40]。 在奖励事件之后，海马体细胞会逆序重新激活，这使得一个动作序列获得的最终价值迅速与其中每个状态-动作对相关联 [7]。
• 人类和动物利用多种学习、记忆和决策系统，每个系统最适合不同的环境 [5, 33]。例如，当环境的准确模型可用，并且有足够的时间和工作记忆资源时，最好的策略是与前额叶皮层相关的 model-based planning [5]。 然而，当没有时间或资源可用于规划时，必须采用计算密集度较低的即时决策系统 [29]。 这在学习新环境的早期就提出了一个问题，因为在这种情况下model-free决策系统会更加不准确，因为它还没有足够的重复经验（repeated experience）来学习准确的价值函数。相比之下，这是 model-free episodic control 可能最有用的情况。因此，海马体参与 model-free control 的观点（argument）与其参与 model-based control 的观点相似。这两种情况下，这种 instance-based 快速学习控制策略都用作训练速度较慢、更具概括性的决策系统 训练过程中的粗略近似值[16]
• episode control 的适用范围可能会因世界的复杂性而受到非常严重的限制。 在真实环境中，很少（如果有的话）重新面对完全相同的情况。在 RL 任务中，重复访问完全相同的状态也极为罕见。 本文中我们展示了常用的 Atari 环境没有这个特点。事实上，我们表明在这项工作中开发的Agent在 10-60% 的时间内重新遇到完全相同的 Atari 状态。 正如预期的那样，episode control 方法在这种情况下运行良好。相较于此，episode control 方法的关键测试是要看他是否也可以在更现实的环境中工作，这种环境中状态永远不会重复，对相似状态的泛化能力非常关键。重要的是，我们还表明，我们的episode control模型在这种基本上永远不会重新访问相同的状态的（3D）环境中仍然表现良好。

2. The episodic controller

• 在强化学习中 [e.g. 37]，agent 通过状态 $s_t\in \mathcal{S}$ ；动作 $a_t\in \mathcal{A}$；和奖励 $r_{t+1}\in \mathbb{R}$ 序列与环境交互；agent的策略 $\pi (a_t|s_t)$ 决定了动作 $a_t$ 的概率分布。agent的目标是学习最大化期望折扣收益 $R_t={\sum }_{\tau =1}^{T-t}{\gamma }^{\tau -1}{r}_{t+\tau }$ 的策略，其中 $T$ 是每个轨迹结束的时间步，$\gamma \in (0,1]$ 是折扣率。agent在状态 $s_t$ 处执行动作 $a_t$ ，使得状态转换到 $s_{t+1}$

• 具有确定性（deterministic）状态转换和奖励的环境在日常经验中很常见。例如，当你退出房间然后返回时，你通常会到达原先的房间。RL算法或大脑可以利用自然环境的这种特性。然而，大多数现有的可扩展深度强化学习算法（例如 DQN [23] 和 A3C [22]）并没有这样做。它们的设计考虑了更一般的环境。因此，原则上，它们可以在状态转移和奖励方面具有高度随机性的设置下运作。 这种普适性是以更长的学习时间为代价的。DQN 和 A3C 都试图找到最大化期望收益的策略。而评估预期回报时，需要许多样本才能获得准确的估计。此外，梯度下降学习进一步减慢了这些算法的速度，通常与在环境中采取行动的速度同步。

• 考虑到现实世界中普遍存在这种确定性情形（near-deterministic situations），如果大脑不采用专门的学习机制来利用这种结构，从而在这种情况下更快地学习，那将是令人惊讶的。我们在这里提出的基于实例的记忆性学习（hippocampal instance-based learning）的 episodic controller 模型就是这样一种机制。它是一个非参数模型（non-parametric model），可以快速记录和重放迄今为止从给定开始状态产生最高回报的动作序列。在最简单的形式中，它是一个增长表（growing table），由状态和动作作为索引。类似RL的价值函数，我们把该表表示为 $Q^{EC}(s,a)$。 每个条目包含通过从状态 $s$ 采取行动 $a$ 获得的最高回报。

• 对于给定状态，episode control policy 为从 $Q^{EC}$ 中具有最高价值的动作。在每个轨迹结束时，$Q^{EC}$ 根据收到的回报进行以下更新
  $$Q^{EC}(s_t,a_t)\leftarrow \{\begin{array}{rlrl}& R_t& & ,if(s_t,a_t)\notin Q^{EC}\\ & max\{Q^{EC}(s_t,a_t),R_t\}& & ,otherwise\end{array}\text{\hspace{1em}(1)}$$
  这里 $R_t$ 是在 $s_t$ 处执行动作 $a_t$ 后获取的折扣收益（discounted return），注意(1)式不是一个通用RL学习目标，因为 $Q^{EC}$ 中存储的价值永远不会减少，不适用于在随机性环境（stochastic environments）下选择合理动作（rational action）

  • 注：如果一个策略只选择具有最高 $Q^{EC}$ 值的动作，将在随机环境中产生强烈的风险寻求行为。相反，也可以删除 max 运算符并直接存储 $R_t$，这样会产生不太乐观的估计，并且在初步实验中表现更差。

• 表格型 RL 方法有两个关键缺陷：

  1. 对于大型问题，它们会消耗大量内存
  2. 它们缺乏对相似状态进行泛化的方法。

  为了解决第一个问题，我们设定一个表格尺寸上限，在达到上限时删除最近最少更新的条目，从而限制表的大小。 这种对较旧的、不常访问的记忆的遗忘也发生在大脑中 [8]。

• 在大规模 RL 问题（例如现实生活）中，新的状态很常见；现实世界一般来说也有这个属性。为了解决新状态下该做什么以及如何在常见经验中概括价值的问题，我们将 $Q^{EC}$ 作为一个非参数化的最近邻模型（non-parametric nearest-neighbours model）。让我们假设状态空间 $\mathcal{S}$ 中存在距离度量。对于从未访问过的状态，通过对 k 个最近状态的 $Q^{EC}$ 价值求平均来近似其 $Q^{EC}$ 价值。因此，如果 s 是一个新状态，那么 $Q^{EC}$ 估计为
  $$\widehat{Q^{EC}}(s,a)=\{\begin{array}{rlrl}& \frac{1}{k}\sum _{i=1}^k{Q}^{EC}(s^{(i)},a)& & if(s,a)\notin Q^{EC}\\ & Q^{EC}(s,a)& & otherwise\end{array}\text{\hspace{1em}(2)}$$
  其中 $s(i),i=1,2,...,k$ 是与状态 $s$ 最近邻的 k 个状态

  • 注：在实践中，我们为每个动作 $a\in \mathcal{A}$ 设置一个 KNN 缓冲区，通过在每个缓冲区中找到与状态 s 最接近的 k 个状态来实现这一点。

• 算法 1 描述了 model-free episodic control 的最基本形式。该算法有两个阶段。
  

  1. 第一阶段，使用由 $Q^{EC}$ 诱导的策略执行一个完整的轨迹，记录每一步收到的奖励。首先将来自环境的每个观察值 $o_t$ 通过嵌入函数（embedding function）$\varphi$ 投影到状态空间中的合适状态，即 $s_t=\varphi (o_t)$，然后根据 $Q^{EC}$ 选择具有最高估计收益（return）的动作。
  2. 第二阶段，通过向后向重放过程（backward replay process）把轨迹的奖励、动作和状态关联到 $Q^{EC}$ 以改进策略（就是反向逐步计算return $R_t$，然后根据式(1)更新）。有趣的是，这种反向重放过程是 [7] 所示的海马体状态清醒反向重放的潜在算法实例，尽管到目前为止，我们还不知道有任何实验测试了海马体的这种有趣用途。

• episodic controller 根据 $Q^{EC}$ 中记录的折扣收益采取行动，试图重放成功的动作序列并重现过去的成功。因此，存储在 $Q^{EC}(s,a)$ 中的值不对应于预期回报的估计，而是基于所看到的状态、奖励和行动，对给定状态和行动的最高潜在回报的估计。在利用比探索更重要，且环境中的噪音相对较小的情况下，根据这样的价值函数运算和行动很有用。

3. Representations

• 在大脑中，海马体对一种表征（representation）进行操作，其中尤其包括腹侧流（ventral stream）的输出 [3, 15, 38]。因此，它有望沿着该表示空间的维度进行泛化 [19]。类似地，特征映射函数 $\varphi$ 对 episodic control 算法遇到新状态时如何执行发挥着关键作用。

  • 注：理解这一点的一种方法是，特征映射 $\varphi$ 决定了从状态空间到基于 episodic controller 的 k近邻算法推出（implied）的 Voronoi cells 的动态离散化（dynamic discretization）。

• 虽然可以使用原始观察空间（observation space），但这在实践中可能行不通。例如，我们在第 4 节中考虑的环境中的每一帧将占用大约 28 KB 的内存，实验总共需要超过 300 GB 的内存。相反，我们考虑将两种不同的观察-状态空间映射函数 $\varphi$，每个 $\varphi$ 在设置 $Q^{EC}$ 估计器的归纳偏差时都具有非常独特的属性。

• 减少内存和计算需求的一种方法是使用从原始观测空间到较低维空间的随机投影，即 $\varphi :x\to A\text{A}Ax,A\text{A}A\in {\mathbb{R}}^{F\times D},F\ll D$，其中 D 是观测的维度。对于从标准高斯分布抽取条目组成的随机矩阵 $A\text{A}A$，Johnson-Lindenstrauss 引理意味着这种变换近似地保留了原始空间中的相对距离 [10]。我们希望这种表示可以使原始观察空间的微小变化对应于潜在收益（return）的微小变化。

• 对于某些环境，观测空间的许多方面与价值预测无关。例如3D 环境中的照明和纹理表面（第 4 节中的迷宫）、2D 环境中的滚动背景（第 4 节中的 River Raid）通常可能无关紧要。在这些情况下，原始观察空间中的小距离可能与动作值中的小距离无关。若能提取更抽象的状态空间表示（例如 3D 几何或 2D 视频游戏中的精灵位置），可能会引出更合适的距离计算方法。抽象特征可以通过使用隐变量概率模型来获得。变分自动编码器（VAE；[12, 30]）在关于图像的各种无监督学习问题中显示出很大的希望（在补充材料中有进一步描述）。有趣的是，VAEs 以无监督方式学习的潜在表征，可以依赖于结构良好的流形（well structured manifolds），捕获变化的主要因素（salient factors of variation） [12，图 4(a) 和 (b)]； [30，图 3(b)]。 在我们的实验中，我们在随机行动 agent 的帧上训练 VAE。使用不同的数据源会产生不同的 VAE 特征，原则上来自一项任务的特征可以用于另一项任务。此外，还可以学习用于比较嵌入映射（观察-状态空间映射）的距离度量。我们将这两个有趣的扩展留给未来的工作。

4. Experimental results

• 我们在两种环境中测试了我们的算法：Atari 环境 Arcade Learning Environment [2] 和第一人称三维环境Labyrinth [22] 的。训练过的agent的视频可在线获取。
  • 注：https://sites.google.com/site/episodiccontrol/
• Arcade Learning Environment 是一套街机游戏，最初为 Atari-2600 终端开发。这些游戏在视觉上相对简单，但需要复杂而精确的策略来实现高预期奖励 [23]。
• Labyrinth（迷宫环境）提供了更复杂的视觉体验，但策略相对简单，例如在存在特定视觉提示时转动。三个迷宫环境都是觅食任务，奖励结构（reward structures）分别设定为有食欲的、反感和稀疏食欲的。
• 对于每个环境，我们分别测试了两个episode controller的性能，它们使用不同的观测-状态映射 $\varphi$ ：
  1. 观测像素值上的 64 个随机投影
  2. VAE 中潜在维度上的后验高斯近似的 64 个参数

4.1 Atari

• 对于 Atari 实验，我们考虑了五款游戏：Ms.PAC_MAN、Q*bert、River Raid、Frostbite 和 Space Invaders。我们将我们的算法与原始 DQN 算法 [23]、具有优先重放的 DQN [31] 以及异步优势 actor-critic [22] (A3C) 以及一种SOAT策略梯度方法进行了比较。依照[23]，观测结果被缩放到 84 x 84 像素并转换为灰度。Atari 模拟器每秒产生 60 个观测（帧）。为了减少计算要求，每个动作重复 4 次，因此agent每秒与环境交互15次。一个小时的游戏大约相当于 200,000 帧。

• 在episode controller中，每个动作的状态-价值二元组缓冲区的尺寸限制为一百万个条目。如果缓冲区已满并且必须引入新的状态-价值二元组，则丢弃最近最少使用的状态的记录。k 近邻查找设置为 k = 11。折扣率设置为 $\gamma =1$。使用 $ϵ=0.005$ 的 $ϵ$-greedy 策略实现探索。我们发现更高的探索率并不是那么有益，因为更多的探索使得开发已知的东西变得更加困难。注意，先前文章给出探索概率（例如，[22, 23]）至少要高出十倍。 因此有趣的是，我们的方法在相对较少的随机探索的范围内获得了良好的性能。

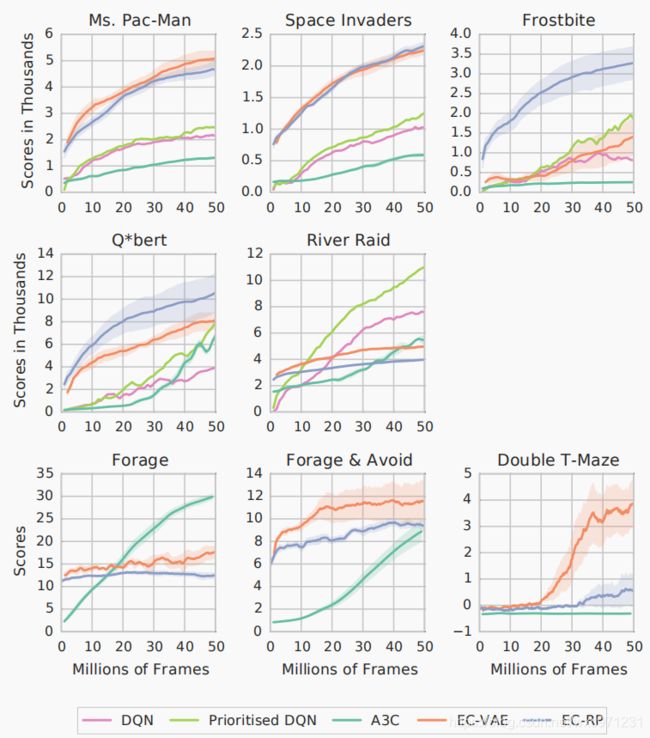
• 如图 1 的前两行所示。在数据效率方面，episode controller在所有游戏的初始学习阶段优于所有其他算法。 在 Q*bert 和 River Raid 游戏中，episode controller最终被一些参数化控制器（图 1 中未显示）取代。在快速学习的初始阶段之后，episode controller 受到了限制，因为随着轨迹变长，在每个轨迹中获得的新经验相对数量会减少。 相比之下，参数化控制器可以利用其非局部泛化能力（ non-local generalisation capabilities）来处理游戏的后期阶段。

• 图 1：五个 Atari 游戏和三个迷宫环境的平均奖励与帧数（单位为百万）的关系。 深色曲线显示了用不同随机数种子初始化的五次运行的平均值（只有一次运行的结果可用于 DQN 基线）。 浅色阴影显示了运行中平均值的标准误差。在学习的初始阶段，episode controller（橙色和蓝色曲线）优于参数化 Q-function 估计器（浅绿色和粉红色曲线）和 A3C（深绿色曲线）。VAE曲线在100万帧后开始，以说明他们的训练使用随机策略
• 两种不同的观测-状态映射（随机投影和 VAE）对episodic control策略的性能没有显着影响。两种表征（representation）都证明了比参数化策略数据效率更高。唯一的例外是 Frostbite，其中 VAE 特征的表现明显更差。 这可能是由于随机策略无法在游戏中到达很远的地方，导致 VAE 的训练集非常差。
• Deep Q-networks 和 A3C 在 Atari环境 中策略改进缓慢。对于 Frostbite 和 Ms.PAC_MAN 来说，这有时被归因于幼稚的探索技术 [13, 28]。我们的结果表明，当与能够与 one-shot fashion 学习的系统相结合时，像 $ϵ$-greedy 这样的简单探索技术可以带来更快的策略改进。
• Atari 环境具有确定性的状态转移和奖励。每个episode从三十个可能的初始状态之一开始。因此，相当大比例的状态-动作二元组在 Q-value 的缓冲区中完全匹配：Frostbite（10%）； Q*bert（60%），Ms.PAC_MAN（50%），Space Invaders（45%），River Raid（10%）。 下一节中，我们将报告在一组更真实的环境中进行的实验，在这些环境中，很少会遇到两次相同的状态。

4.2 Labyrinth

• 迷宫实验涉及三个levels（屏幕截图如图 2 所示）。环境中每个模拟物理时间秒执行 60 次观测（帧）。观测结果是尺寸为 84 x 84 像素的灰度图像。agent每秒与环境交互15 次（动作会自动重复 4 帧以减少计算要求）。代理有八种不同的可用动作（向左移动、向右移动、向左转、向右转、向前移动、向后移动、向前并向左转、向前并向右转）。
  
  • 图 2：迷宫环境的高分辨率屏幕截图。 (a) Forage and Avoid 显示了苹果（正面奖励）和柠檬（负面奖励）。(b) Double T-maze在转折点显示线索（cues）。© Double T-maze的顶视图。线索（cues）表明奖励位于左上角。
• 在episode controller中，每个动作的状态-价值二元组缓冲区的尺寸限制为10万个条目。当缓冲区已满并且必须引入新的状态值对时，最近最少使用的状态的记录被丢弃。k 近邻参数设置为 k = 50。折扣率设置为 $\gamma =0.99$。 探索是通过使用 $ϵ=0.005$ 的 $ϵ$-greedy 策略实现的。我们使用 A3C [22] 作为基线。迷宫关卡具有确定性的状态转移和奖励，但初始位置和面向方向是随机的，并且环境更加丰富，是三维的。出于这个原因，与 Atari 不同，Labyrinth 上的实验在 $Q^{EC}$ 值的缓冲区中遇到的精确匹配很少；三个levels均低于 0.1%
• 每个级别都逐渐变得更加困难。第一级称为 Forage，要求agent尽快收集苹果，每个苹果提供 1 的奖励。一个简单的策略就是转向直到看到一个苹果然后朝它移动就足够了。图 1 显示episode controller非常快速地找到了寻找苹果的策略。最终A3C 赶上并胜过episode controller，得到了更有效的捡苹果策略。
• 第二个级别，称为 Forage and Avoid，agent收集苹果仍然获得 1 的奖励，同时要避免收集会导致 -1 奖励的柠檬。该级别如图 2(a) 所示。 这个级别只需要比 Forage 稍微复杂一点的策略（相同的策略加上避免柠檬），但 A3C 需要超过 4000 万步才能赶上episode controller在不到 300 万帧中就到达的性能。
• 第三个级别，称为 Double-T-Maze，要求智能体在一个有四个末端的迷宫中行走（地图如图 2c 所示），其中一个末端包含一个苹果，而其他三个包含柠檬。在每个路口，代理都会看到一个颜色提示，指示苹果所在的方向（见图 2b）：红色代表左边，绿色代表右边。agent穿过柠檬会得到 -1 的奖励；穿过苹果会得到 1 的奖励，被传送回起始位置，并重新采样苹果的位置。每个episode的持续时间限制为 1 分钟，如果agent解决任务足够快，它可以多次到达苹果。Double-T-Maze 是一个困难的 RL 问题：奖励稀疏。 事实上，A3C 从未实现过高于零的预期回报。由于双 T 迷宫级别的稀疏奖励性质，agent在状态空间中随机漫游，少数获得奖励的情况下，A3C没有足够强地更新策略。相比之下，episode controller在这些实例上表现出类似于一次性学习（one-shot learning）的行为，并且能够从包含任何非零奖励的极少数episode中学习。这使得episode controller在观察 20 到 3000 万帧后学到具有正预期回报的策略，而参数化策略从未学到过预期回报高于零的策略。在这种情况下，episodic control方法在稀疏奖励环境中快速提升性能，因为它迅速锁定了有效的策略。

4.3 Effect of number of nearest neighbours on final score

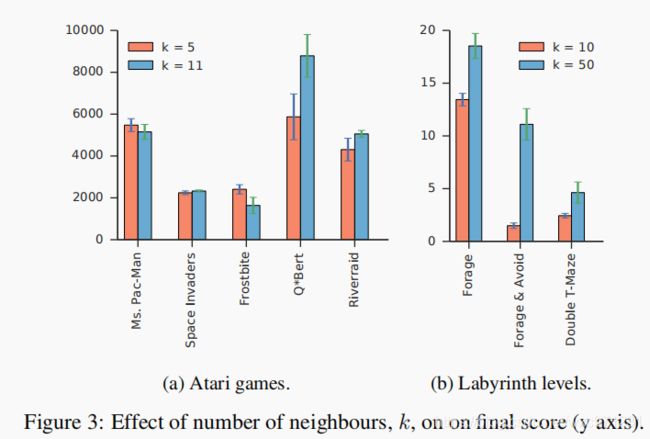
• 最后，我们使用 VAE 特征比较了 k（最近邻的数量）的变化对 Labyrinth 和 Atari 任务的影响。在我们上面的实验中，注意到在 Atari 环境中重新访问相同的状态是很常见的，而且随机投影的表现通常与 VAE 特征相同或更好。另一个更有趣的特征是，随着近邻数量的增加，除了在 Q*bert 游戏中 VAE 表现不错（见图 3a），在 Atari 游戏上学习的 VAE 不会产生更高的分数。 在Labyrinth levels上，智能体很少遇到相同的状态，我们观察到 VAE 的表现优于随机投影。
• 有趣的是，对于这种情况，在 Labyrinth levels 中增加最近邻数量对代理的最终性能有显着影响（见图 3b）。这强烈表明 VAE 特征为 episode control agent 提供了迷宫中的泛化能力。
  

5. Discussion

• 这项工作解决了当前强化学习系统的一个关键缺陷，即它们无法以 one-shot 方式进行学习。我们提出了一种基于非参数记忆经验的快速学习系统，并表明它可以比参数化的函数逼近器更快地学习好的策略。然而，我们的方法可能会在训练后期阶段被参数化方法超越。我们希望这些想法能够在实际系统中得到应用，并产生高效利用数据的 model-free 方法。
• 这些结果也支持了大脑可以使用 episodic controllor 的假设，尤其是在新环境中学习的早期阶段。另请注意，在某些情况下，episodic controllor 总是会表现出色。例如当隐藏食物供以后食用时，某些鸟类（如松鸦）最好准确记住它们的藏身之处，而不是根据可能位置的分布进行搜索 [4]，这些因素支持大脑使用多个控制系统和仲裁机制来确定在每个时间点采取行动的模型 [5, 16]。
• 我们将这种方法称为无模型情节控制（model-free episodic control），以将其与基于模型的情节规划（model-based episodic planning）区分开来。我们推测，除了众所周知的，分别与背外侧纹状体和前额叶皮层相关的习惯性和目标导向系统（habitual and goal-directed systems）外，大脑还可以使用这两种策略 [5]。
• 这项工作呈现的初步图景是，可用于决策的时间和工作记忆资源是哪些控制策略可用的关键决定因素。当必须快速做出决策时，基于规划的方法（planning-based）根本不是一种选择。这种情况下，唯一的选择是习惯性无模型系统（habitual model-free system）或情节无模型系统（episodic model-free system）。当决策不那么匆忙时，基于规划的方法变得可用，然后大脑必须在使用语义（新皮质）信息的规划或使用情节（海马体）信息的规划之间进行仲裁。在这两种时间机制中，是否使用 episodic 信息的关键决定因素是较慢的学习系统提供的估计中还有多少不确定性。在系统之间的统计权衡方面，该预测与 [5, 16] 的预测一致，它以他们的工作为基础，强调了仓促决策和工作记忆资源不足的潜在影响[29]。这些想法可以通过控制决策时间或工作记忆的实验来验证，也许可以通过正交任务实验（orthogonal tasks），在不同统计条件下快速测量内侧颞叶和输出结构之间的一致性。

附录：用于表示学习的VAE

• 变分自编码器 (VAE; [12, 30]) 是受压缩理论启发的潜在变量概率模型。一个 VAE（如图 4 所示）由两个人工神经网络组成：
  1. 编码器，它接受观测并将它们映射到消息中；
  2. 解码器，接收消息并近似恢复观测结果。
     VAE 旨在最小化通过通信通道将观测值从编码器传输到解码器的成本。为了最小化传输成本，VAE 必须学会捕获观测分布的统计数据 [例如 17]。出于我们的表征学习目的，我们使用编码器网络作为我们的特征映射 $\varphi$。 对于几个数据集，VAE 编码器学习的表示已被证明可以捕获数据潜在生成过程中变化的独立因素 [11]
• 更详细地说，编码器接收观察值 $x\text{x}x$，并输出消息分布的参数值 $q(z|x=x\text{x}x)$。通信通道（communication channel）通过消息的先验分布 $p(z)$ 来确定消息的成本。解码器接收从 $q(z|x=x\text{x}x)$ 中随机抽取的消息 $z\text{z}z$，并通过输出观测值上的分布参数 $p(x|z=z\text{z}z)$ 对其进行解码。VAE 训练时要最小化的（准确恢复原始观察的）成本，为预期通信成本 $KL(q(z|x\text{x}x)||p(z))$ 和预期校正成本 $E[p(x=x\text{x}x|z)]$ 之和。
• 在我们所有的实验中，$x\in {\mathbb{R}}^{7056}$（84 x 84 灰度像素，范围为 [0, 1]），$z\in {\mathbb{R}}^{32}$。我们选择具有对角协方差矩阵的高斯分布作为 $q(z|x)$、$p(z)$ 和 $p(x|z)$ 。
• 在所有实验中，
  1. 编码器网络有四个卷积层 [14] ，分别使用 {32, 32, 64, 64} 内核，内核大小 {4, 5, 5, 4}，内核步幅（kernel strides） {2, 2, 2, 2} ， 无填充（no padding）以及非线性ReLU [25] 。卷积层之后是 512 个 ReLU 单元的全连接层，线性层从中输出近似后验 q(z|x) 的均值和对数标准差。
  2. 解码器设置为编码器的镜像，先是具有 512 个 ReLU 单元的全连接层，然后是四个反向卷积层 [6]，分别具有 {64, 64, 32, 32} 内核，内核大小为 {4, 5, 5, 4}， 内核步幅 {2, 2, 2, 2}，无填充，然后是具有两个输出内核的反向卷积：一个用于均值，一个用于 $p(x|z)$ 的对数标准差。如果网络输出的值较小，则 $p(x|z)$ 中每个维度的标准偏差不设置为0.05。
     在每个环境上执行随机策略获得一百万个观察结果，训练 VAE 来模拟它们。优化 VAE 的参数时，使用 RmsProp 优化器 [39]，步长设为 1e-5，minibatches size设为100，批量运行 400,000 步随机梯度下降。
     

个人总结

• 假设人在玩超级玛丽游戏，只要有一次人按下了跳键之后，可以跳起来躲避敌人，那么人马上就可以用上这条经验，在下次遇到敌人的时候就会按下跳键。甚至，人还能将经验广义化，不仅是这种类型的敌人，还有别的类型的敌人，甚至障碍，人都可以应对。在机器学习中，这种情况被称为 one-shot learning

• 本文试图把 one-shot learning 引入Deep RL。传统深度强化学习无法执行one-shot learning，这是因为使用神经网络来泛化状态价值，但由于 “底层策略或价值函数的梯度更新（gradient-based updates）很缓慢，这些算法需要大量的步骤来吸收（assimilate）这些信息并将其转化为策略性能的提升”

• 作者认为过去的 deep RL 方法为了保证随机性环境中的普适性而牺牲了效率，在确定性环境下，估计价值函数可以比较简单和高效。为此

  1. 作者受人脑海马体学习启发，试图给 agent 引入非参数记忆。海马体被认为是基于案例学习的，它可能是根据动作的奖赏把对应的状态存储起来，后续根据实际的状态，把对应的处理动作找出来，这可以表示为一张增长表。于是作者放弃深度网络，直接用了一个表格型方法，表中存储每个状态动作的最高价值。式子（1）的更新就相当于把TD方法中的学习率设为 $\alpha =1$，并且更新时仅保留较高价值，这样价值估计速度非常快，但是仅适用于确定性环境（“利用比探索更重要，且环境中的噪音相对较小”）。这个表格可以看作 agent 的非参数化记忆信息，它表示每个状态动作 “最好可能有多好”
  2. 去掉深度网络后就无法泛化状态价值了，作者做了两个处理，一是假设状态空间中有存在距离度量，使用KNN来做价值泛化，二是设定表格大小上限，引入“遗忘机制”。

• 接下来作者考虑了如何对 agent 的观测进行编码（就是利用文中的嵌入映射 $\varphi$），因为原始观测太占内存，需要编码后作为状态。作者考虑了两个方法

  1. 随机采样：近似地保留了原始观测空间中的相对距离
  2. VAE编码自编码器：提取更抽象的状态空间表示

  作者发现良好的编码方式也有助与提升泛化性能

• 最后，作者认为 model-free episodic control 和 model-based episodic planning 是跟人的大脑里面基于习惯和基于目标两种机制联系在一起的。到底启用那种机制取决于时间和资源

  1. 当时间和记忆资源充足时，我们大可在脑海对可能的动作和情况进行多次预演/规划，然后执行最优动作。这涉及到基于语义目标的高级思维过程，是在大脑额叶完成的。这种情况下我们可以使用 model-based episodic planning。举个例子，在迷宫寻路问题中，这时就可以直接用最短路算法解，因为我们对环境有着清晰的认识（注意这时我们已经完成了环境建模）
  2. 当时间和记忆资源不足时，比如刚刚面对一个新任务时，我们就无法进行上述的规划，只能进行一些试错，同时我们在海马体中形成对这些尝试的价值记忆。这时用本文的 model-free episodic control 方法就比较好。

句子摘抄

1. Humans, on the other hand, can very quickly exploit highly rewarding nuances of an environment upon first discovery.
   另一方面，人类则可以在第一次探索时就迅速发现并利用环境中高回报的细微差异

2. Here we investigate whether a simple model of hippocampal episodic control can learn to solve difficult sequential decision making tasks.
   本文中，我们研究了一个简单的海马轨迹控制模型能否学习解决困难的顺序决策任务

3. We demonstrate that it not only attains a highly rewarding strategy significantly faster than state-of-the-art deep reinforcement learning algorithms, but also achieves a higher overall reward on some of the more challenging domains.
   我们证明，它不仅比SOAT深度强化学习算法更快地学到了高回报的策略，而且在一些更具挑战性的领域中获得了更高的整体回报（overall reward）

4. This paper addresses the question of…
   本文解决了…问题

5. Thus these algorithms lack the ability to rapidly latch onto successful strategies
   因此，这些算法缺乏快速锁定成功策略的能力

6. Humans and animals utilise multiple learning, memory, and decision systems each best suited to different settings
   人类和动物利用多种学习、记忆和决策系统，每个系统最适合不同的环境

7. The key test for this approach is whether it can also work in more realistic environments where states are never repeated and generalisation over similar states is essential
   episode control 方法的关键测试是要看他是否也可以在更现实的环境中工作，这种环境中状态永远不会重复，对相似状态的泛化能力非常关键

8. Critically, we also show that our episodic control model still performs well in such (3D) environments where the same state is essentially never re-visited.
   重要的是，我们还表明，我们的episode control模型在这种基本上永远不会重新访问相同的状态的（3D）环境中仍然表现良好。

9. Thus, in principle, they could operate in regimes with high degrees of stochasticity in both transitions and rewards.
   因此，原则上，它们可以在状态转移和奖励方面具有高度随机性的设置下运作

10. By analogy（类比） with RL value functions, we denote this table $Q^{EC}(s,a)$
    类似RL的价值函数，我们把该表表示为$Q^{EC}(s,a)$

11. In large scale RL problems (such as real life) novel states are common
    在大规模 RL 问题（例如现实生活）中，新的状态很常见

12. The values stored in $Q^{EC}(s,a)$ thus do not correspond to estimates of the expected return, rather they are estimates of the highest potential return for a given state and action, based upon the states, rewards and actions seen.
    因此，存储在 $Q^{EC}(s,a)$ 中的值不对应于预期回报的估计，而是基于所看到的状态、奖励和行动，对给定状态和行动的最高潜在回报的估计

13. We expect this representation to be suffificient when small changes in the original observation space correspond to small changes in the underlying return.
    我们希望这种表示可以使原始观察空间的微小变化对应于潜在收益（return）的微小变化。

14. A feature extraction method capable of extracting a more abstract representation of the state space (e.g. 3D geometry or the position of sprites in the case of 2D video-games) could result in a more suitable distance calculation.
    一种能够提取更抽象的状态空间表示（例如 3D 几何或 2D 视频游戏中的精灵位置）的特征提取方法可能会引出更合适的距离计算方法

15. Variational autoencoders (VAE; [12, 30]), further described in the supplementary material, have shown a great deal of（大量的） promise across a wide range of unsupervised learning problems on images.
    变分自动编码器（VAE；[12, 30]）在关于图像的各种无监督学习问题中显示出很大的希望（在补充材料中有进一步描述）

16. Interestingly, the latent representations learnt by VAEs in an unsupervised fashion can lie on well structured manifolds capturing salient factors of variation
    有趣的是，VAEs 以无监督方式学习的潜在表征，可以依赖于结构良好的流形（well structured manifolds），捕获变化的显着因素

17. Furthermore, the distance metric for comparing embeddings could also be learnt
    此外，还可以学习用于比较嵌入映射的距离度量

18. the 64 parameters of a Gaussian approximation to the posterior over the latent dimensions in a VAE.
    VAE 中潜在维度上后验高斯近似的 64 个参数

19. The agents interact with the environment 15 times per second, as actions are repeated 4 times to decrease the computational requirements
    为了减少计算要求，每个动作重复 4 次，因此agent每秒与环境交互15次

20. We found that higher exploration rates were not as benefificial, as more exploration makes exploiting what is known harder.
    我们发现更高的探索率并不是那么有益，因为更多的探索使得开发已知的东西变得更加困难

21. In terms of data effificiency the episodic controller outperformed all other algorithms during the initial learning phase of all games.
    在数据效率方面，episode controller在所有游戏的初始学习阶段优于所有其他算法

22. Our results demonstrate that a simple exploration technique like $ϵ$-greedy can result in much faster policy improvements when combined with a system that is able to learn in a one-shot fashion.
    我们的结果表明，当与能够以一次性方式（one-shot fashion）学习的系统相结合时，像 $ϵ$-greedy 这样的简单探索技术可以带来更快的策略改进。

23. In this case, episodic control thrived in sparse reward environment as it rapidly latched onto an effective strategy
    在这种情况下，episodic control方法在稀疏奖励环境中快速提升性能，因为它迅速锁定了有效的策略。

24. The tentative picture to emerge from this work is one in which the amount of time and working memory resources available for decision making is a key determiner of which control strategies are available.
    这项工作呈现的初步图景是，可用于决策的时间和工作记忆资源是哪些控制策略可用的关键决定因素。