Activation Function（激活函数） 持续更新...

---

什么是激活函数

在神经元中，输入的 inputs 通过加权，求和后，还被作用了一个函数，这个函数就是激活函数 Activation Function。

为什么需要激活函数？

引入非线性函数作为激活函数，这样深层神经网络表达能力就更加强大（不再是输入的线性组合，而是几乎可以逼近任意函数），这样神经网络就可以应用到众多的非线性模型中。

绝大多数神经网络借助某种形式的梯度下降进行优化，激活函数需要是可微分（或者至少是几乎完全可微分的）。此外，复杂的激活函数也许产生一些梯度消失或爆炸的问题。因此，神经网络倾向于部署若干个特定的激活函数。

Identity

通过激活函数 Identity，节点的输入等于输出。它完美适合于潜在行为是线性（与线性回归相似）的任务。当存在非线性，单独使用该激活函数是不够的，但它依然可以在最终输出节点上作为激活函数用于回归任务。

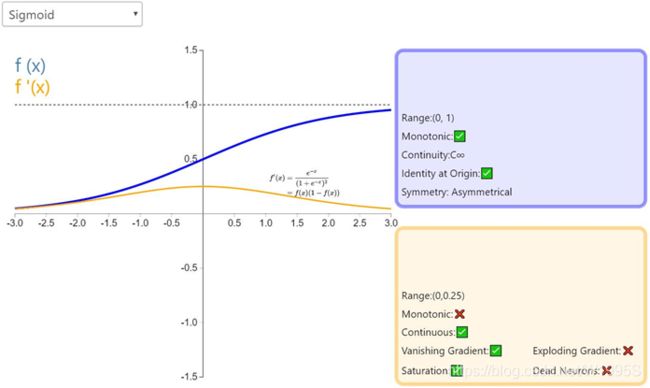
Sigmoid

Sigmoid函数，也就是logistic函数，对于任意输入，它的输出范围都是（0,1），很像平滑版的阶跃函数。公式如下：

优点：

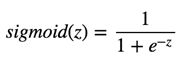
1. 平滑，易求导。单调连续，输出范围有限，优化稳定，可以用作输出层。它在物理意义上最为接近生物神经元。
2. 不同于二值化输出，sigmoid 可以输入 0 到 1 之间的任意值。可以用来表示概率值。
3. 与 2 相关，sigmoid 的输出值在一个范围内，这意味着它不会输出无穷大的数。

缺点：

1. 激活函数计算量大（在正向传播和反向传播中都包含幂运算和除法），尽管有人说，与矩阵乘法或卷积相比，激活函数在深度网络的计算是非常小的一部分，所以这可能不会成为一个大问题。不过，我认为这值得一提。反向传播求误差梯度时，求导涉及除法；
2. 当神经元的激活在接近0或1处时会饱和，在这些区域梯度几乎为0，这就会导致梯度消失，Sigmoid导数取值范围是[0, 0.25]，由于神经网络反向传播时的“链式反应”，很容易就会出现梯度消失的情况，几乎就有没有信号通过神经传回上一层。如果我们初始化神经网络的权值为 [0,1] 之间的随机值，由反向传播算法的数学推导可知，梯度从后向前传播时，每传递一层梯度值都会减小为原来的0.25倍，例如对于一个10层的网络， 根据0.25¹⁰≈0.000000954，第10层的误差相对第一层卷积的参数W1的梯度将是一个非常小的值，梯度在穿过多层后将变得非常小接近于0，即出现梯度消失现象
3. Sigmoid的输出不是0均值（即zero-centered）；这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入，那么关于w的梯度在反向传播的过程中，将会要么全部是正数，要么全部是负数，这将会导致梯度下降权重更新时出现z字型的下降。随着网络的加深，会改变数据的原始分布。

梯度消失在深度学习中是一个十分重要的问题，我们在深度网络中加了很多层这样的非线性激活函数，这样的话，即使第一层的参数有很大的变化，也不会对输出有太大的影响。换句话讲，就是网络不再学习了，通常训练模型的过程会变得越来越慢，尤其是使用梯度下降算法时。

Tanh

类似于 sigmoid 函数，它也将输入转化到良好的输出范围内。对于任意输入，tanh 将会产生一个介于 -1 与 1 之间的值。


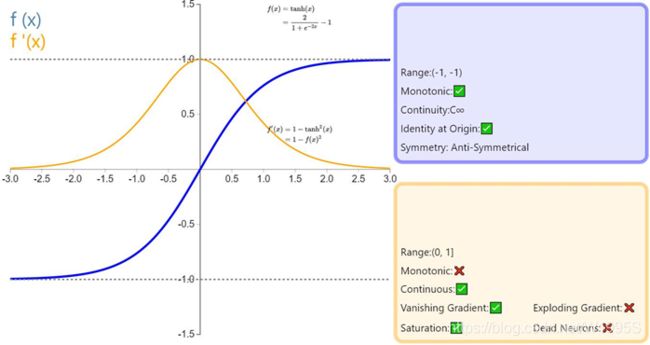
相比Sigmoid函数，

1. tanh的输出范围时(-1, 1)，解决了Sigmoid函数的不是zero-centered输出问题； 比Sigmoid函数收敛速度更快，因为 Tanh 的输出均值比 Sigmoid 更接近 0。
2. 幂运算的问题仍然存在；
3. tanh导数范围在(0, 1)之间，相比sigmoid的(0, 0.25)，梯度消失（gradient vanishing）问题会得到缓解，但仍然还会存在。

为了防止饱和，现在主流的做法会在激活函数前多做一步batch normalization，尽可能保证每一层网络的输入具有均值较小的、零中心的分布。

ReLU

ReLU 从数学表达式来看，运算十分高效。对于某一输入，当它小于 0 时，输出为 0，否则不变。下面是 ReLU 的函数表达式。Relu(z) = max(0,z)

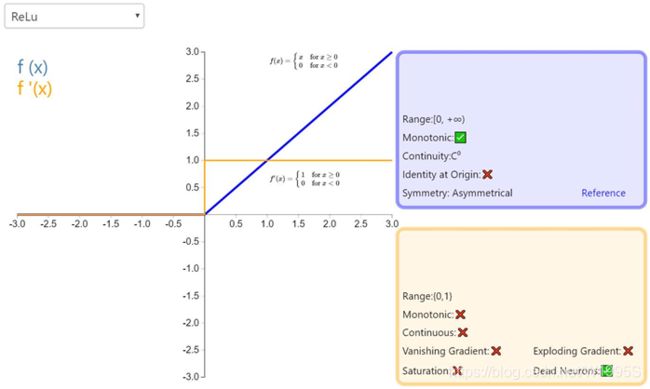
优点：

1. 相较于sigmoid和tanh函数，ReLU对于SGD随机梯度下降的收敛有巨大的加速作用；sigmoid和tanh在求导时含有指数运算，而ReLU求导几乎不存在任何计算量。
2. ReLU在x>0下，不会饱和，导数为常数1的好处就是在“链式反应”中保持梯度不衰减，从而缓解梯度消失问题，但梯度下降的强度就完全取决于权值的乘积，这样就可能会出现梯度爆炸问题。解决这类问题：一是控制权值，让它们在（0，1）范围内；二是做梯度裁剪，控制梯度下降强度，如ReLU(x)=min(6, max(0,x))
3. ReLU在x<0下，ReLU硬饱和，输出置为0的特点：描述该特征前，需要明确深度学习的目标：深度学习是根据大批量样本数据，从错综复杂的数据关系中，找到关键信息（关键特征）。换句话说，就是把密集矩阵转化为稀疏矩阵，保留数据的关键信息，去除噪音，这样的模型就有了鲁棒性。ReLU将x<0的输出置为0，就是一个去噪音，稀疏矩阵的过程。而且在训练过程中，这种稀疏性是动态调节的，网络会自动调整稀疏比例，保证矩阵有最优的有效特征。

缺点：

1. 随着训练的推进，部分输入会落入硬饱和区x<0，导致对应权重无法更新。这种现象被称为“神经元死亡”，更确切地说，当神经元在向前传递中激活函数输出为零时，就会出现这个问题，导致它的权值将得到零梯度。因此，当我们进行反向传播时，神经元的权重将永远不会被更新，而特定的神经元将永远不会被激活。
2. ReLU 强制将x<0部分的输出置为0（置为0就是屏蔽该特征），可能会导致模型无法学习到有效特征，所以如果学习率设置的太大，就可能会导致网络的大部分神经元处于永久死亡状态，所以使用ReLU的网络，学习率不能设置太大。
3. ReLU的输出不是zero-centered

ReLU目前仍是最常用的activation function，在搭建人工神经网络的时候推荐优先尝试！

Leaky ReLU，PReLU（Parametric Relu）, RReLU（Random ReLU）

为了防止模型的‘Dead’情况，后人将x<0部分并没有直接置为0，而是给了一个很小的负数梯度值α。

LReLU 中的α为常数，一般设置 0.01。这个函数通常比 Relu 激活函数效果要好，但是效果不是很稳定，所以在实际中 Leaky ReLu 使用的并不多。

PRelu（参数化修正线性单元） 中的α作为一个可学习的参数，会在训练的过程中进行更新。

RReLU（随机纠正线性单元）也是Leaky ReLU的一个变体。在RReLU中，负值的斜率在训练中是随机的，在之后的测试中就变成了固定的了。RReLU的亮点在于，在训练环节中，aji是从一个均匀的分布U(I,u)中随机抽取的数值。

ReLU及其变体图像：

Softmax

Softmax用于多分类神经网络输出，目的是让大的更大。函数公式是


就是如果某一个 zj 大过其他 z, 那这个映射的分量就逼近于 1,其他就逼近于 0，主要应用就是多分类。

为什么要取指数，第一个原因是要模拟 max 的行为，所以要让大的更大。
第二个原因是需要一个可导的函数。

Softmax是Sigmoid的扩展，当类别数k＝2时，Softmax回归退化为Logistic回归。

sigmoid ，ReLU， softmax 的比较

Sigmoid 和 ReLU 比较：

sigmoid 的梯度消失问题，ReLU 的导数就不存在这样的问题，它的导数表达式如下：

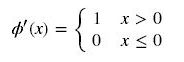
曲线如图

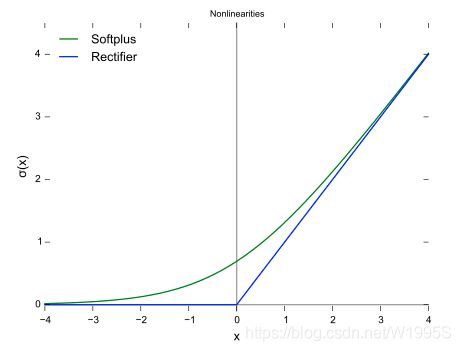
对比sigmoid类函数主要变化是：
1）单侧抑制
2）相对宽阔的兴奋边界
3）稀疏激活性。

Sigmoid 和 Softmax 区别：

softmax is a generalization of logistic function that “squashes”(maps) a K-dimensional vector z of arbitrary real values to a K-dimensional vector σ(z) of real values in the range (0, 1) that add up to 1.

sigmoid将一个real value映射到（0,1）的区间，用来做二分类。而 softmax 把一个 k 维的real value向量（a1,a2,a3,a4….）映射成一个（b1,b2,b3,b4….）其中 bi 是一个 0～1 的常数，输出神经元之和为 1.0，所以相当于概率值，然后可以根据 bi 的概率大小来进行多分类的任务。

二分类问题时 sigmoid 和 softmax 是一样的，求的都是 cross entropy loss，而 softmax 可以用于多分类问题

softmax是sigmoid的扩展，因为，当类别数 k＝2 时，softmax 回归退化为 logistic 回归。具体地说，当 k＝2 时，softmax 回归的假设函数为：

利用softmax回归参数冗余的特点，从两个参数向量中都减去向量θ1 ，得到:

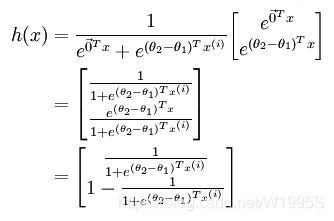
最后，用 θ′ 来表示 θ2−θ1，上述公式可以表示为 softmax 回归器预测其中一个类别的概率为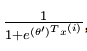

另一个类别概率的为

这与 logistic回归是一致的。

softmax建模使用的分布是多项式分布，而logistic则基于伯努利分布
　　
多个logistic回归通过叠加也同样可以实现多分类的效果，但是 softmax回归进行的多分类，类与类之间是互斥的，即一个输入只能被归为一类；多个logistic回归进行多分类，输出的类别并不是互斥的，即"苹果"这个词语既属于"水果"类也属于"3C"类别。

ELU

指数线性单元（Exponential Linear Units，ELU），

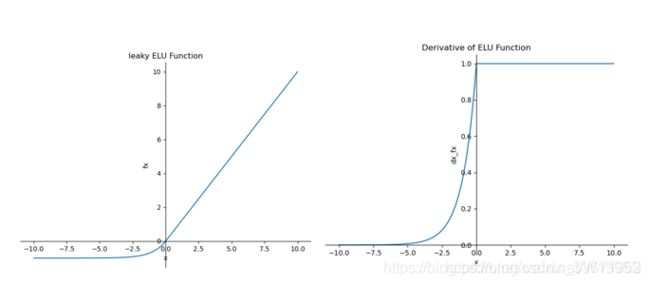
特点：ELU具备了ReLU的优点，解决了ReLU的死区现象，ELU输出均值接近0，但是ELU中含有指数操作，计算量也相应增加。通常，ELU的超参数α=1。
优点：
（1）ELU具备了ReLU的优点：解决了sigmoid和tanh函数梯度消失的问题；相较于sigmoid和tanh函数的指数运算，ReLU计算更快；ReLU收敛速度比sigmoid和tanh函数约快6倍左右。
（2）解决了ReLU的死区现象
（3）ELU输出均值接近0
缺点：ELU中含有指数操作，计算量增加

Swish

Swish 在深层模型上的效果优于 ReLU。可以看做是介于线性函数与ReLU函数之间的平滑函数.例如，仅仅使用 Swish 单元替换 ReLU 就能把 Mobile NASNetA 在 ImageNet 上的 top-1 分类准确率提高 0.9%，Inception-ResNet-v 的分类准确率提高 0.6%。


β是个常数或可训练的参数，Swish 具备无上界有下界、平滑、非单调的特性。


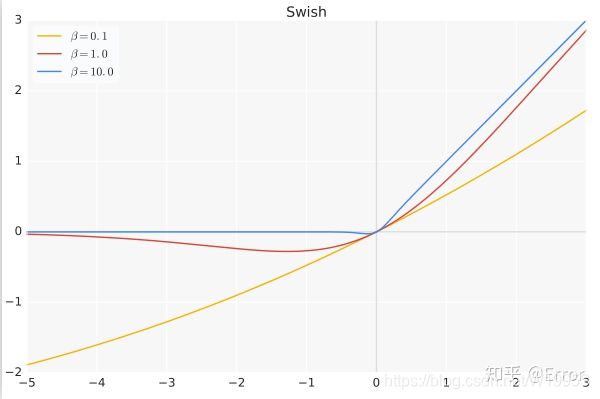
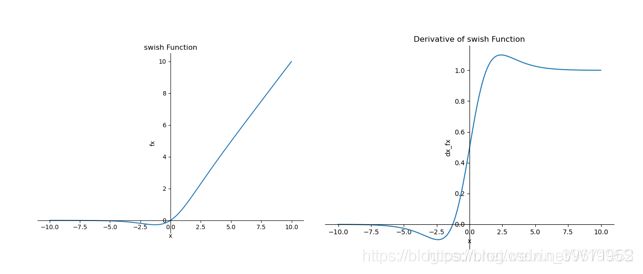
特点：Swish 具备无上界有下界、平滑、非单调的特性。
优点：ReLU有无上界和有下界的特点，而Swish相比ReLU又增加了平滑和非单调的特点，这使得其在ImageNet上的效果更好。
缺点：引入了指数函数，增加了计算量

Mish

一种自正则的非单调神经激活函数，平滑的激活函数允许更好的信息深入神经网络，从而得到更好的准确性和泛化。根据论文实验，该函数在最终准确度上比Swish(+0.494%)和ReLU(+ 1.671%)都有提高。



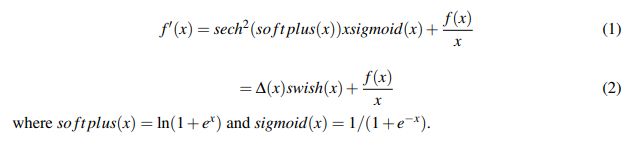
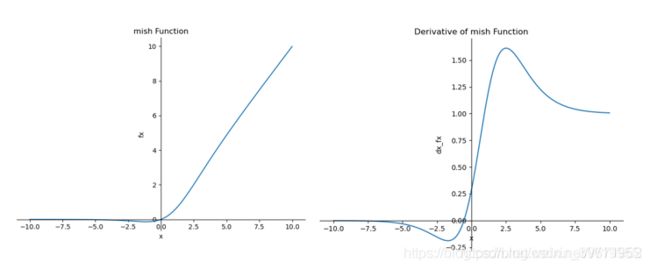
特点：无上界(unbounded above)、有下界(bounded below)、平滑(smooth)和非单调(nonmonotonic)。

• 无上界：可以防止网络饱和，即梯度消失。 有下界：提升网络的正则化效果。
  平滑：首先在0值点连续相比ReLU可以减少一些不可预料的问题，其次可以使网络更容易优化并且提高泛化性能。
  非单调：可以使一些小的负输入也被保留为负输出，提高网络的可解释能力和梯度流

优点：平滑、非单调、上无界、有下界
缺点：引入了指数函数，增加了计算量

# torch中代码实现
class Mish(nn.Module):
    def __init__(self):
        super().__init__()
        print("Mish avtivation loaded...")

    def forward(self,x):
        x = x * (torch.tanh(F.softplus(x)))
        return x

如何选择

选择的时候，就是根据各个函数的优缺点来配置，例如：

如果使用 ReLU，要小心设置 learning rate，注意不要让网络出现很多 “dead” 神经元，如果不好解决，可以试试 Leaky ReLU、PReLU 或者 Maxout.

常见激活函数对比

激活函数使用小Tips:

1、除非输出层是二分类问题，尽量不要使用sigmoid函数；
2、tanh函数几乎适合所有的场景
3、最常用的激活函数是ReLU，不确定用哪个激活函数就用ReLU试试看