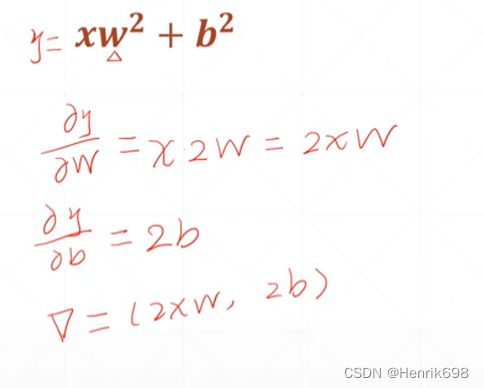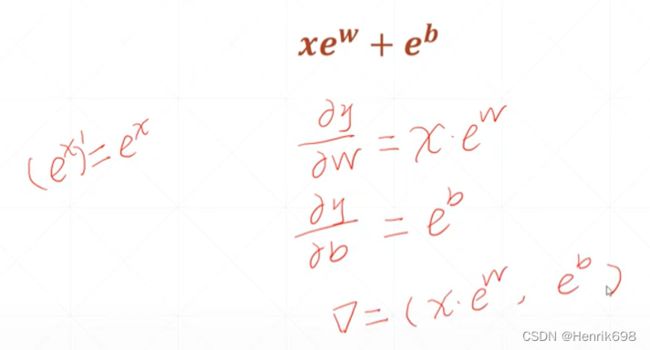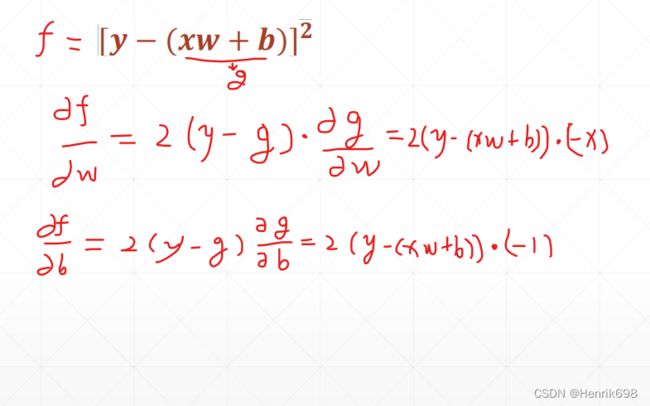PyTorch-04梯度、常见函数梯度、激活函数Sigmoid；Tanh；ReLU及其梯度、LOSS及其梯度、感知机（单层感知机）、感知机2（多输出的）、链式法则、MLP反向传播推导、2D函数优化实例

PyTorch-04梯度、常见函数梯度、激活函数（Sigmoid、Tanh、ReLU）及其梯度、LOSS及其梯度（MSE 均方误差、Cross Entropy Loss 交叉熵损失函数和两种求导方法）、感知机（单层感知机模型）、感知机2（多输出的）、链式法则、MLP(Multilayer Perceptron多层感知机) 反向传播推导、2D函数优化实例

一、什么是梯度

阐述Clarification——梯度

▪ 导数(derivate)
导数就是与梯度最为相近的一个东西。
一个函数的导数，被定义为一个函数在x处的变化量（即在x处的斜率），导数反应的是y的值随x的变化趋势。导数本身是一个标量，它反应的是一个变化的程度。任意方向上的长度表示变化率（导数方向是可以随意指定的，如下图红线所绘制的），因此是一个标量，长度反应变化率的大小。导数可以用d来表示。

▪ 偏微分(partial derivate)
偏微分讲的是一个函数对其自变量的变化率的描述程度。偏微分也是一个标量。它与导数不同，导数是一个非常宽泛的概念，导数方向是可以随意指定的，而偏微分是给定的自变量的方向。偏微分是导数的一种特殊情况，偏微分指定了方向的，方向就是自变量的方向，这个函数有多少个自变量，就有多少个偏微分。偏微分可以用∂来表示。

例如：下图z的函数：
如果对x求导，则将x看做是自变量，y就会被视为常数，因此结果是-2x。
如果对y求导，则将y看做是自变量，x就会被视为常数，因此结果为2y。

▪ 梯度(gradient)
梯度就被定义为所有自变量的偏微分所组成的一个向量。注意梯度是一个向量，而不是标量。

例如：就下图z的函数：

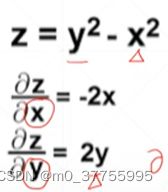
梯度为对x的偏微分和对y的偏微分所组成的向量，如果求在x=0,y=0处的梯度，将x=0,y=0带入到梯度向量中，就可以获得在该点的梯度结果。

梯度反应的是什么呢（梯度意义是什么呢）？What does grad mean?

梯度与导数有不同的区别，梯度是有方向的，此外梯度还有大小。

重要：函数的梯度是一个向量，向量的方向代表这个函数在当前点的增长方向，这个向量的模（即向量的长度）代表这个函数在当前这个点增长的速率。

下图所示，x和y表示两个自变量，z轴为函数的输出轴（反应函数的大小），下面的小箭头反应的是这个函数在x、y的梯度，每个箭头都有一个方向（即梯度所指的方向），其梯度方向代表该函数增长的方向；以及箭头的长度（梯度的大小，即梯度的模），其长度反应一种变化的趋势，模越大变化的趋势越显著。

如何搜索最小值？How to search for minima?

如何利用梯度的这些信息找到极值解呢？
一般情况下，我们搜索的是一个极小值解。如果想要搜索极大值，可以将loss变为负号，这样就可以通过搜极小值解来找到极大值解了。

下图所示，通过每次更新函数的参数，这个函数的当前值θt，减去一个▽f(θt)梯度的方向，该梯度的方向要乘上一个α (learning rate （学习率） 学习率决定了权值更新的速度，一般我们设置这个数会比较小0.001)，通过这种迭代更新的方式，可以帮助函数找到一个极小值的解。

例如：特殊情况局部极小值，造成随机选取的自变量θ1和θ2不在跟新。
下图中function函数的梯度为 ▽ = (2θ1, 2θ2) 。
第一步，随机的初始化θ1和θ2，这里θ1初始化为0，θ2初始化为0。
第二步，求出梯度的情况，即（0,0）
第三步，更新出来后为(0,0)
发现这个可能是局部极小值，局部极小值是要找的点，因此就不在跟新了。说明我们初始化的θ1=0，θ2=0就是其极小值，因此函数在该极小值下的梯度为0，所有就不会跟新了，这也是偶然的巧合。

通用1维可视化过程Learning process-1

查看曲线图，函数为f(x) = (x^2) *sin(x)，其自变量只有一个x，1维的，因此就是在1维函数上面x轴代表x，y轴代表的就是这个函数f(x)的值。

首先，我们随机初始化一个点，x=2.5。x=2.5处所对应梯度的值为-9左右（即只有一个自变量所以derivative导数=partial derivate偏微分值=gradient梯度值）。

此外，如果按照下面的公式图，xt = 2.5 - α (-9)，如果不乘 α 学习率，则xt = 2.5 - (-9) = 11.5，这样xt就会取到非常远的值，错过了很多值。所以为了要让xt的取值平滑，这里一定要让梯度乘以α学习率，让xt有较小的变化，这里α学习率取0.005，-9 * 0.005 = -0.045，xt = 2.5 - (-0.045) = 2.545。通过这个方法，让xt不断的更新，更新到xt点所对应的梯度为0（即偏微分为0），找到我们所要的一个解。

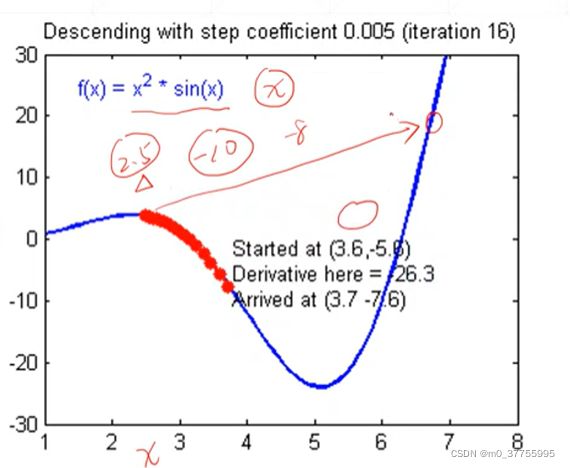
通用2维可视化过程Learning process-2

自变量是x和y，因此是一个二维的平面。每一条曲线代表不同的优化算法。

该过程的核心依然是θt+1 = θt - αt ▽f(θt)，这里的梯度▽f(θt)是一个向量，其具有方向性，通过这个特性，最终可以找到五角星所在的全局最小值。但是在寻找全局最小值的过程中，可以发现绿色线和紫色线的两个算法最开始走偏了，找到了局部最小值点后，又回头找到了全局最小值。

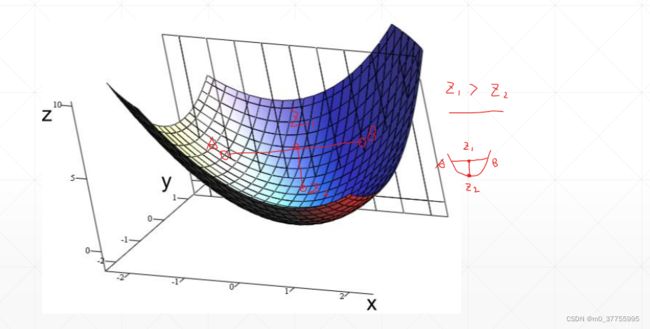
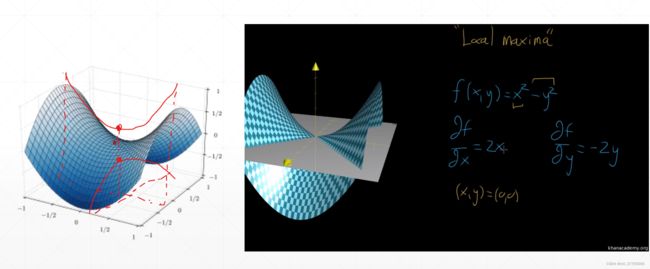
凸函数 Convex function 全局最优解

对于任何维的函数，任意选取点A、B，A与B两点连线后的中点Z1，并从中点Z1向函数做垂线，并相交于Z2，总是有Z1>Z2，这样的函数就称为凸函数。凸函数是肯定可以找到全局最优解的。

局部最小解 Local Minima

一个函数可能存在多个局部最小值点的情况。
初始化为A点时，所找到的可能是A’点，该点是局部最小点。
初始化为B点时，所找到的可能是B’点，该点时全局最小点。

残差神经网络ResNet-56

残差神经网络的主要贡献是发现了“退化现象（Degradation）”，并针对退化现象发明了 “快捷连接（Shortcut connection）”，极大的消除了深度过大的神经网络训练困难问题。
左侧的那个曲面是ResNet-56的loss平面，是非常粗糙的，及时可以看到有一个全局最小值解也是很难找到的，很有可能陷入其他无数多个局部最小值中。对于深层次的神经网络（比如说156层），我们要去搜索很有可能找到的表现不是很满意，因为当前所找到的解可能是局部最小值解，这样获得的网络精度不是特别的高。
如果在神经网络旁边添加一条支路，该支路称为shortcut模块，类似于物理电路中的短接一样，神经网络可以变得很深，优化的也很好，精度也会比以往好很多。添加了支路之后可视化的平面是右侧图的效果，发现loss平面变得平滑了，对于平滑后的这个平面，可以很好的任意选择一个点开始，能够很快的找到全局最小值。

鞍点 Saddle point

使用梯度来搜索最小值时，除了遇到局部最小值，更多的还会遇到一个saddle point鞍点。鞍点是在x和y这两个维度来说，一个是局部最大值，一个是局部最小值。这个点就是鞍点，这个点在取到x这个维度时为局部最小值点，而取到y这个维度时是局部最大值。鞍点出现时，会让搜索卡在这个点上，无法很好的搜索出全局最小值点。鞍点是比局部最小值更可怕的情况。

影响优化器的性能的因素 Optimizer Performance

除了局部最小值和鞍点会影响我们的优化器（即搜索的过程），那么还有哪些因素会影响搜索的过程呢？
▪ initialization status 初始状态
▪ learning rate 学习率
▪ momentum 动量（即怎么逃离局部最小值）
▪ etc.

Initialization
初始状态的不同，对我们的搜索影响是很大的。所以初始状态很重要。如果初始化没有把握，就按照目前主流的初始化的方法即可，也就是何恺明的初始化方法。

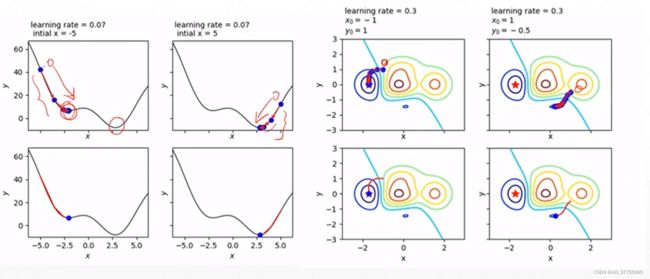
不同的初始化状态，会得到不同的结果：
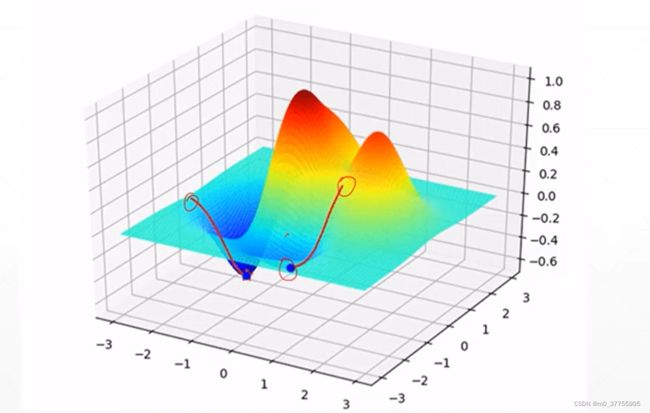learning rate
learning rate设置过大，会造成步长过长。大部分情况，如果步长很大会造成神经网络不收敛了。

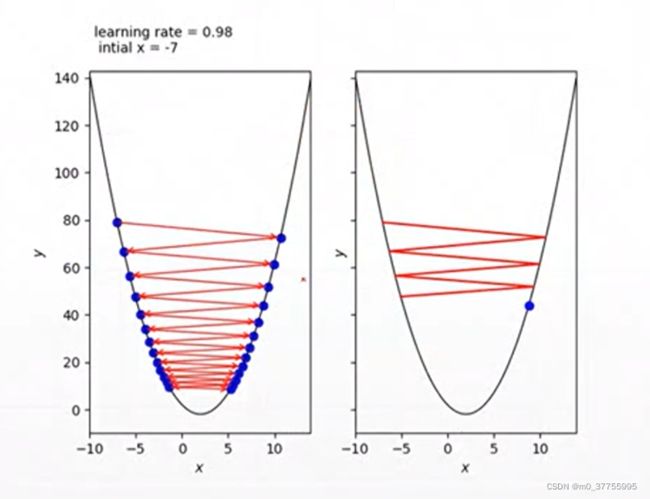
逃离局部最小值 Escape minima（添加一个momentum动量）
添加一个动量，可以理解为惯性，会冲出局部最小值。

二、常见函数梯度

常见函数Common Functions梯度的求导方法（即常见函数的导数）

这些梯度会在日后的神经网络中推导过程中会用得到。对于基本函数的求导方法要有所掌握

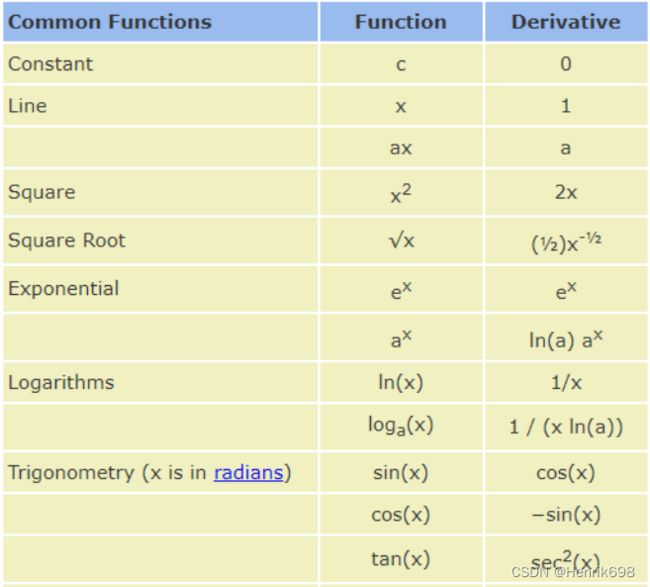
+ b

常数对于自变量的导数肯定是0。
感知机线性模型的偏微分(梯度)的求解。

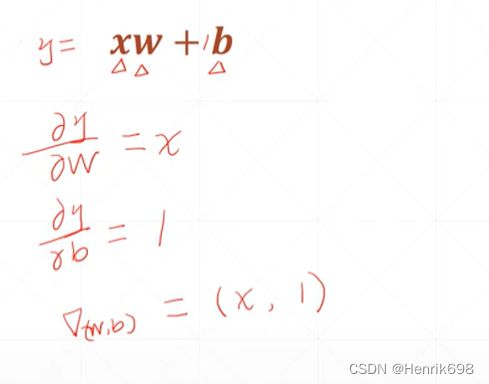
² + ²

二次模型的梯度求解方式。

ʷ + ᵇ

指数的梯度求解方式。其中eˣ的导数还是eˣ。

[ − ( + )]²

线性感知机的输出与真实label之间的均方差。

log( + )

(logₑˣ)’ = 1/x

三、激活函数（Sigmoid、Tanh、ReLU）及其梯度

激活函数Activation Functions来源

其中蓝色圈的加权响应，并不是一个线性的输出，是有一个阈值响应机制的。也就是说，这个响应值的和，小于某一个值的时候，这个青蛙不会有反应；如果响应值大于某一个阈值的时候，这个青蛙会输出一个固定的响应值，注意是一个固定的输出。因此生物学家根据青蛙神经元的机制提出了这样一个阈值函数。这个函数非常简单，就是一个阶梯函数，当小于这个阈值时，就不会有任何响应，如果大于这个阈值时，会有一个固定的输出。

激活函数（单层感知机-激活阶梯函数）

当时的科学家，根据这种机制，衍生出来了一个计算机相应的模型。这个模型与青蛙的神经元响应情况非常相似。

在下图的模型中，Z为x0到xn与其对应的权重乘积后的加权求和，Z并不是一个线性输出，在输出前会有一个阈值函数，在Z小于0时，这个单层的感知机是没有响应的，当Z大于0时，这个神经元机制会输出一个固定的信号值1。这个非常简单的阶梯函数，就是激活函数，激活的意思就是只有Z大于0，这个节点才能够被激活，不然的话这个节点处于睡眠状态。

此外一个重要概念就是，激活函数是不可导的，因为如果函数的导数是不连续的情况，则这个函数是不可导，激活函数在Z=0处的导数是与Z大于0导数和Z小于0导数产生了不连续，因此该函数是一个不可导的情况，因此这个函数不能直接使用梯度下降的方法来进行优化。
在当时，使用启发式搜索的方法来求解单层感知机最优解的情况。

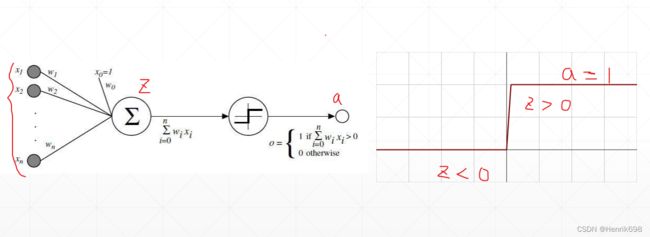
Sigmoid / Logistic

为了解决单层感知机-激活阶梯函数不可导的情况，科学家提出了一个连续的光滑的这样的一个函数sigmoid或者logistic逻辑回归。

激活函数：Sigmoid

sigmoid函数特点：
Z=0的时候，这个函数取到了一个中间值0.5，Z大于0函数会慢慢逼近于1，Z小于0函数会慢慢逼近于0。这个sigmoid函数比较光滑，适合模拟生物学中神经元的机制。也就是说Z比较小时，就慢慢接近于一个不响应的状态，即a=0；当Z变得很大的时候，这个响应也不会变得很大，因为这个生物响应的机制是固定的，所以a会慢慢接近于1，因此这个就有点像压缩的功能。会将Z从负无穷到正无穷所对应的值压缩到一个有限的空间(0,1)。

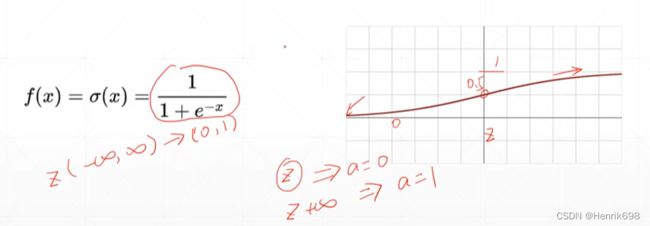
sigmoid函数导数情况：

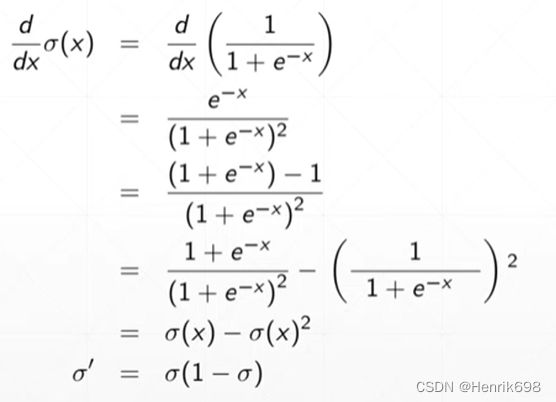
sigmoid函数是神经网络中的一部分，sigmoid是的值是已知的，这样可以很快求得sigmoid函数的导数。sigmoid这个激活函数使用的非常多，主要是因为其连续的、光滑的，而且函数值压缩在0到1这个范围中，我们很多时候都需要0到1这样一个范围，比如说probability概率，为了得到概率，我们就可以用sigmoid函数将输出值压缩到0到1这个区间。

sigmoid函数存在一个严重的问题：
使用sigmoid函数有一个问题，在Z无限大时所对应的函数的导数就为0，即▽f(θt)=0，因此 θt+1 = θt， 长时间无法更新函数的参数，，就是长时间的loss保持不变，使其得不到更新，这种情况叫梯度离散。

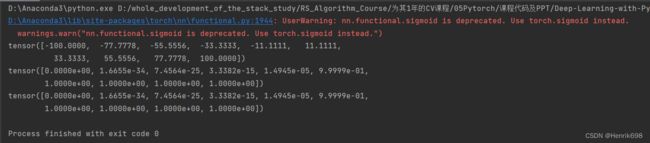
torch.sigmoid

sigmoid函数在pytorch中如何实现：
torch.sigmoid()或者F.sigmoid() (这里的F，是from torch.nn import functional as F)。

import torch
from torch.nn import functional as F

z = torch.linspace(-100,100,10)
print(z)

#两种方法调用sigmoid()函数：
print(torch.sigmoid(z))
print(F.sigmoid(z))

激活函数Tanh

Tanh函数特点：
Tanh这个激活函数在RNN（循环神经网络）中使用比较多，Tanh的表达式与sigmoid函数不一样，但Tanh其实可以由sigmoid函数变化而来，x轴平面压缩1\2，在y轴放大两倍(0,2)，再减常数1(即y轴向下平移一个单位长度)，这样函数值的区间就变成了(-1,1)。

Tanh函数导数情况：
Tanh函数的导数也能像sigmoid函数一样能够很方便的直接求出：

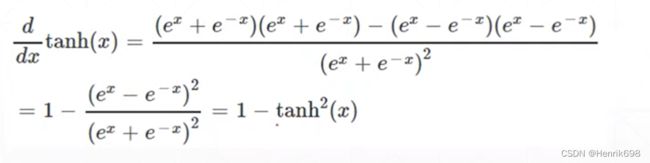
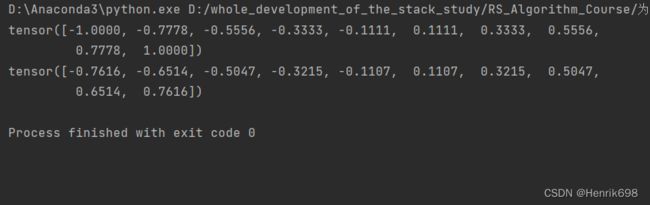
torch.tanh

tanh函数在pytorch中如何实现：

import torch
from torch.nn import functional as F

z = torch.linspace(-1,1,10)
print(z)
print(torch.tanh(z))

激活函数 Rectified Linear Unit（ReLU 线性整流函数 ）整型的线性单元

ReLU 函数特点：
深度学习中奠基的激活函数：Rectified Linear Unit。该函数的使用非常非常简单。当z小于0时就不响应，当z大于0时就线性的响应。ReLU非常适合做Deep Learning。当z小于0时，函数梯度为0，当z大于0时，函数梯度为1。在做向后传播的时候，导数为1，在计算梯度时非常方便，不会放大也不会缩小，使得梯度保持不变。因此在搜索最优解，ReLU函数有一个先天的优势，就是其梯度计算非常的简单，而且没有放大或缩小，使得梯度保持不变，因此就减少了sigmoid函数所出现的梯度离散，梯度爆炸的情况。

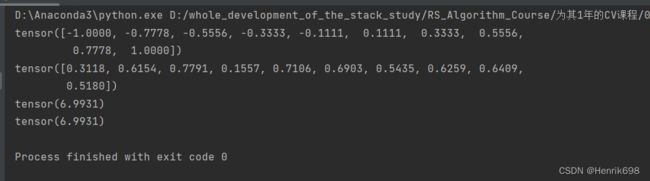
F.relu

ReLU函数在pytorch中如何实现：

import torch
from torch.nn import functional as F

z = torch.linspace(-1,1,10)
print(z)

#两种方法调用relu()函数：
print(torch.relu(z))
print(F.relu(z))

可以注意到当输入的值大于0时，其函数结果就为输入的值，即x=y。基本上做研究，基本上都是优先ReLU函数，遇到额外特殊情况可以尝试一下其他的激活函数。

四、LOSS及其梯度

经典损失 Typical Loss

▪ Mean Squared Error（MSE）
均方误差

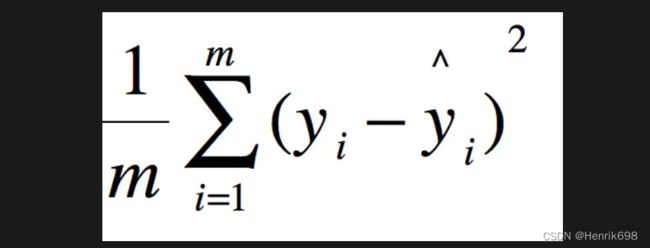
▪ 用于分类的误差 Cross Entropy Loss 交叉熵损失函数
▪ binary 用于二分类
▪ multi-class 也可以用于多分类
▪ +softmax 与softmax这个激活函数搭配来使用的
▪ Leave it to Logistic Regression Part 会在逻辑回归的章节详细讲解 Cross Entropy Loss

MSE

这里需要注意L2-norm与均方根误差（RMSE）相同，L2范数。
RMSE（Root Mean Squard Error）均方根误差。即：(RMSE)^2 = MSE

import torch
from torch.nn import functional as F

z = torch.linspace(-1,1,10)
print(z)
zPre = torch.rand([10])
print(zPre)

#torch.norm()需要传入2个参数
#参数1：真实值减预测值
#参数2：输入2，表示上图中的L2-norm
#这样就获得了均方根误差，如果要获得均方误差就需要在加一个平方.pow(2)
MSE = torch.norm(z - zPre,2).pow(2)
print(MSE)

MSE2 =sum((z-zPre)**2)
print(MSE2)

MSE梯度的求导方式

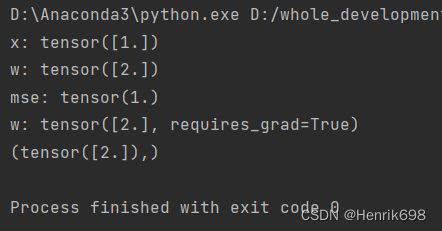
使用pytorch自动求导方法1：autograd.grad

这里y=torch.ones(1)；x = torch.ones(1).float()；w = torch.full([1],2).float()；b=0；ypre = xw + b = 12+0 = 2
mse = (1 - 2)^2 =1
mse的偏导数mse_grad = 2(1-2)*(-1) = 2
发现下面pytorch对mse的偏导数计算结果与我们自己求得的结果相同。

import torch
from torch.nn import functional as F

x = torch.ones(1).float()
w = torch.full([1],2).float()
print('x:',x)
print('w:',w)
#线性模型pred = xw + b,其中x为1，w为2的tensor，b为0
#F.mse_loss()需要两个参数
#第一个参数:predict的值 这里是y=torch.ones(1)
#第二个参数:label值
mse = F.mse_loss(torch.ones(1),x*w)
print('mse:',mse)

# print(torch.autograd.grad(mse,[w])) 
#这里会报错RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn
#对于deep learning就需要传入pred和[w1,w2,...]
#由于报错，我们需要对w进行更新，告诉pytorch，w需要grad梯度这个信息的。

w.requires_grad_() #这里requires_grad后面的下划线"_"，表示会对w进行更新，告诉pytorch，w需要grad梯度这个信息的。
print('w:',w)

# torch.autograd.grad(mse,[w])
#RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn
#这里还是会报错，因为pytorch是一共动态图，是按顺序执行的，所有还需要再次计算mse后执行该行代码。

mse = F.mse_loss(torch.ones(1),x*w)
mse_grad=torch.autograd.grad(mse,[w])
print(mse_grad)

使用pytorch的求导方法2：loss.backward

import torch
from torch.nn import functional as F

x = torch.ones(1).float()
w = torch.full([1],2).float()
print('x:',x)
print('w:',w)
#线性模型pred = xw + b,其中x为1，w为2的tensor，b为0
#F.mse_loss()需要两个参数
#第一个参数:predict的值 这里是y=torch.ones(1)
#第二个参数:label值
mse = F.mse_loss(torch.ones(1),x*w)
print('mse:',mse)

# print(torch.autograd.grad(mse,[w])) #这里会报错RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn
#对于deep learning就需要传入pred和[w1,w2,...]
#由于报错，我们需要对w进行更新，告诉pytorch，w需要grad梯度这个信息的。

w.requires_grad_() #这里requires_grad后面的下划线"_"，表示会对w进行更新，告诉pytorch，w需要grad梯度这个信息的。
print('w:',w)

# torch.autograd.grad(mse,[w])
#RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn
#这里还是会报错，因为pytorch是一共动态图，是按顺序执行的，所有还需要再次计算mse后执行该行代码。

mse = F.mse_loss(torch.ones(1),x*w) #必须完成动态图的建图的过程
#通过F.mse_loss这句话来完成动态图的建图
#在完成建图的过程中pytorch会记录所有建图的路径
#所有通过.backward()可以回溯建图的上一步步骤，这样一致从后往前回溯到最开始，并完成在这个回溯建图上所有tensor需要gradient梯度的计算，其计算出来的gradient不会在返回回来。
mse_grad = mse.backward() #这一步不会像torch.autograd.grad(mse,[w])那样返回出一个list，且list中每一个tensor所对应的grad信息，所有返回的是none，但是grad信息被保留在每个tensor本身上了，只需.grad，就可以产看了。
print(mse_grad)

print(w.grad)

#这里需要特别注意：
#大家在查看消耗传播的时候很有可能就会查看变量w.grad的信息，因此会使用w.grad的信息把tensor打印出来，如果tensor维度特别大，我们会把w.grad.norm()打印出来，这样就从某种上反应了tensor的gradient的norm()的大小。
print(w.norm()) #w.norm()返回的是tensor本身的L2_norm
print(w.grad.norm()) #返回的是w梯度的norm()

上述两种求导方法总结：

第一种是手动细节的求导过程，返回的是一个list，[∂loss/∂w1,∂loss/∂w2,…]，这样每个list就是偏微分的过程。
第二种更加方便的方式是直接在最后的loss调用.backward()方法，其梯度信息不回额外的返回，会赋值在每个需要返回梯度的tensor的grad上面，只需.grad查看即可。

激活函数 Softmax（ Cross Entropy Loss 交叉熵损失函数搭配使用的激活函数softmax）

更多的用于分类的 Cross Entropy Loss 交叉熵损失函数，与cross entropy搭配一起使用的激活函数就是softmax

softmax的作用：
对于三个节点的输出（图片中的 [2.0, 1.0, 0.1] ）：
我们将输出的数值转为概率的话，希望概率最大的那个值所在的索引作为预测值的label，如果要转成概率就必须要人为的压缩到[0,1]这个区间内，我们可以使用sigmoid函数将值压缩到[0,1]这个区间内，但是对于分类问题来说所有概率之后要为1，sigmoid会存在让所有概率之和为3的情况，为了更好的满足要求这里就使用softmax函数。

▪ soft version of max
Softmax函数是一个非线性转换函数，通常用在网络输出的最后一层，输出的是概率分布（比如在多分类问题中，Softmax输出的是每个类别对应的概率），计算方式如下：
可以看到每个p的范围都在[0,1]区间内，所有p的和为1。
此外这个softmax函数还有一个重要特点，就是会将原来输入较大的通过函数输出后会放的更大，而原来较小的则会压缩到较为密集的空间，这样会使得原来最大与最小值之间的差价通过该函数而扩大（输入中2/1=1,输出概率中0.7/0.2=3.5，这个明显扩大了）。

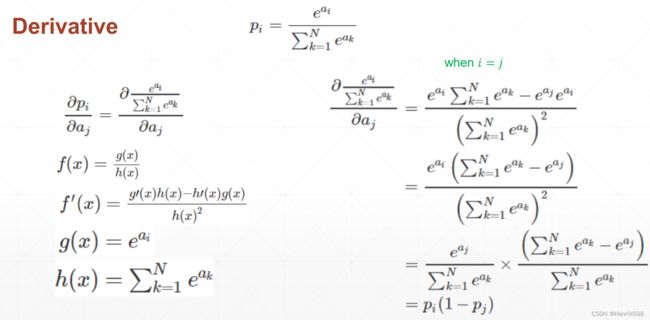
推导softmax的梯度：
当 i = j

当 i != j

总结一下softmax激活函数的求导情况：
i=j 时，偏导为正数；i与j不等时，偏导为负。

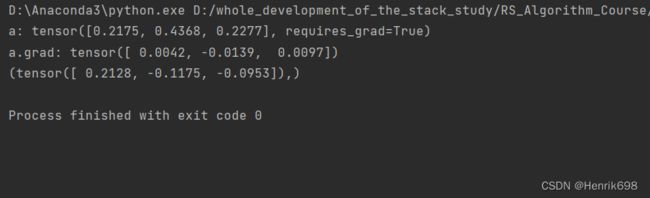
使用pytorch的求导 F.softmax

import torch
from torch.nn import functional as F

a = torch.rand(3,dtype=torch.float)
a.requires_grad_()
print(a)

p = F.softmax(a,dim=0)
#对a进行softmax操作，返回的是probability。
#此外还要指定对哪个维度进行softmax()操作，要在feature这个维度上进行此操。
print(p.backward(retain_graph=True)) #这里会报错

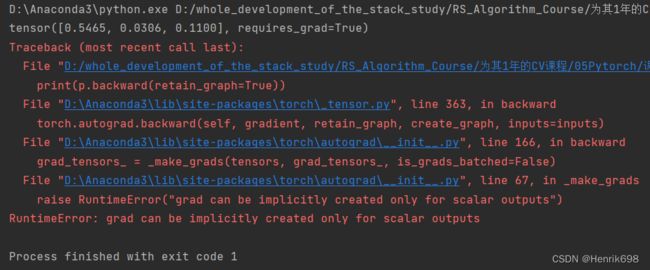
（这个问题解决参考链接：https://blog.csdn.net/qq_39208832/article/details/117415229）
提示报错：RuntimeError: grad can be implicitly created only for scalar outputs
对于标量输出，梯度只能被隐式创建就是说使用.backward()的前提是x必须是标量，而不是向量，如果x是向量，那么，backward函数里就要加参数像这样：

import torch
from torch.nn import functional as F

a = torch.rand(3,dtype=torch.float)
a.requires_grad_()
print('a:',a)

p = F.softmax(a,dim=0)
#对a进行softmax操作，返回的是probability。
#此外还要指定对哪个维度进行softmax()操作，要在feature这个维度上进行此操。
p.backward(torch.rand_like(a),retain_graph=True)
print('a.grad:',a.grad)
#参数retain_graph=True表示这个图不会被清除，可以再使用一次backward获得梯度信息，如果不写这个参数，则第二次再使用backward获得梯度信息会报错。

#参数1：求导的因变量（需要求导的函数）。loss必须是只有一个量，否则会报错。
#这里参数1是对p的第二个输入进行求导
#参数2：为求导的自变量
print(torch.autograd.grad(p[0],[a],retain_graph=True))
#可以注意到输出，当i=j，则输出为正数，i!=j，则输出为负数，发现输出的是满足要求的。

五、感知机（单层感知机模型）

单层感知机模型

单程感知机的梯度计算和梯度更新的过程：

预测值y就等于：输入节点xi，和其输入节点相对应的权值wi进行相乘，并累加后，在跟一个bias偏置相加。

单层感知机模型Perceptron

由于原来的激活函数是不可导的，所以这里更换成了sigmoid函数作为激活函数。
经过激活函数后的结果与目标值（target,label,标注都是一个意思，为目标值）进行loss损失函数计算。

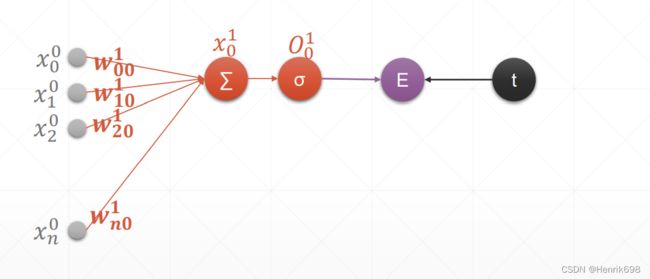
这里需要注意：(下图中)
灰色的图标所有符号上标的表示第0层，下标表示第n个元素的。
橘黄色图标所有符号上标的表示第1层，w的下标分别是i和j，i表示与输入项相对应的上一层节点，j表示下一层第几个求和节点，下图中求和节点只有一个所以w的j都是0。这一层中x的上标表示第1层，下标0表示第一次上的0号节点（因为这里是单层感知机，所以第1层只有一个节点）。之后会经过激活函数进行输出，这个输出值就是O，O的上标1表示第1层，下标0表示第0号节点。
这里E表示Loss损失函数的计算，就是激活函数后的结果与目标值进行均方误差计算。

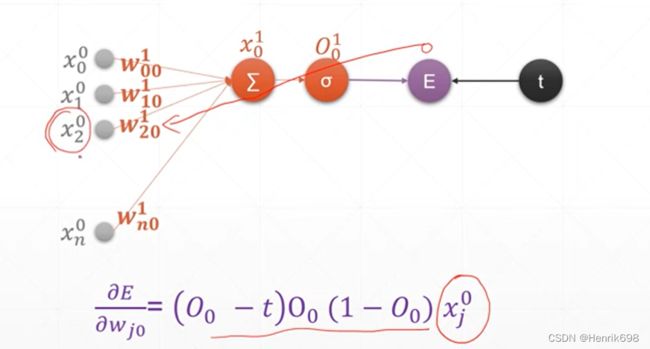
单层感知机的权值的梯度推导

可以注意到红圈的1/2，这个是为了更求导的次方项产生的2进行抵消，其实写不写1/2都是一样的，因为梯度的单调性是不会改变的。



通过这个推导，我们可以总结出，对于单层的感知机的梯度为：

pytorch来计算单层感知机的权值的梯度

import torch
from torch.nn import functional as F

x = torch.rand(1,10)
print('输入x：',x)
w = torch.randn(1,10,requires_grad=True)
print('权值w:',w)
print('权值矩阵w转至',w.t())

#@表示矩阵计算，x为1行10列的矩阵，w.t()为w矩阵的转至为10行1列
o = torch.sigmoid(x@w.t())
print('sigmoid函数处理后的情况',o)
print('o.shape:',o.shape)

loss = F.mse_loss(torch.ones(1,1),o)
print('loss:',loss) #loss是一个标量
print(loss.shape)

loss.backward()

print(w.grad) #获得了w权值向量每个元素的偏导数

# w' = w -learningRate* ▽w 这样就能更新单层感知机的权值了
#通过不断的更新，最终可以获得一个合适的w，使得x*w 越来越接近y真实值。

六、感知机2（多输出的）

单层感知机模型的输出节点是一个，这里将输出节点变成多个，就是我们的多输出的感知机。（感知机就被定义为单输出的）
注意下图，
w的下标表示jk，j是上一层的j号输入，k表示输入与权值再求和的第k个输出。
有n个输入x，有m个输出x，mn个链接数量，偏微分计算的数量就是mn个。

对wⱼₖ这个通式进行偏微分的推导（权值的梯度推导）

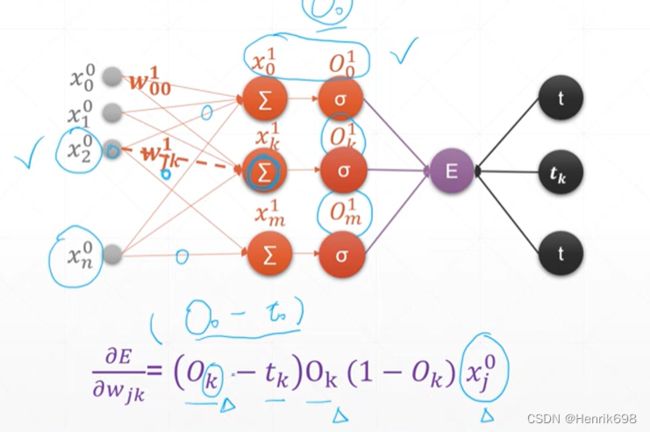
这里可以发现多输出的梯度推导公式仅仅有一点与单层感知机的梯度推导公式不同，那就是小标，单层感知机的梯度公式下标是指定好的，因为其输入和输出是一一对应的，多输出的是下标k是多个输入所对应的，多对一的。
此外对wⱼₖ求偏导，j是对应的输入节点数，k是对应的输出节点数。那么w的shape，w矩阵的行为k对应输出节点数，w矩阵的列为j对应输入节点数。

(这里可以理解为有多少输出节点，w初始时就有多少行；有多少输入节点，w初始时就有多少列，在后面权值w与x输入相乘时，w是要转至的.t() )。

要了解w，b的作用可以查看：https://blog.csdn.net/xwd18280820053/article/details/70681750

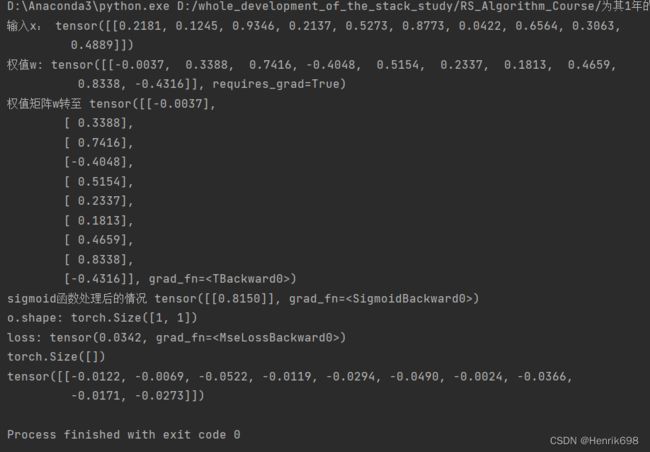
pytorch来计算多输出的权值的梯度

import torch
from torch.nn import functional as F

x = torch.rand(1,10)
print('输入x：',x)
w = torch.randn(2,10,requires_grad=True)
print('权值w:',w)
print('权值矩阵w转至',w.t())

#@表示矩阵计算，x为1行10列的矩阵，w.t()为w矩阵的转至为10行1列
o = torch.sigmoid(x@w.t())
print('sigmoid函数处理后的情况',o)
print('o.shape:',o.shape)

loss = F.mse_loss(torch.ones(1,2),o) #注意输入参数维度必须相同
print('loss:',loss)

loss.backward()
print('w.grad:',w.grad)
print('w.grad.shape:',w.grad.shape)
# w.grad的shape与w的shape是一样的，如果不一样则w' = w - learningrate*▽w中是没法相减的。
# 这里的shape[2,10] 2可以理解为输出节点有2个，10可以理解为有10个输入节点。

多输出的感知机的推导公式，就相当于标准全连接层的输出层的推导公式，下次内容会增加隐藏层。

七、链式法则

神经网络上最重要的公式，链式法则。
通过链式法则，可以将最后一层的误差，一层一层的输出到中间层的权值上面，从而得到中间层的梯度信息，通过这个梯度信息可以很好的更新权值，从而达到一个最优化的效果。

了解链式法则前，先了解一下常用的求导组合公式（两个梯度的和、两个梯度的差、乘积、除法、）：

其中最后一个就是链式法则的表达形式。

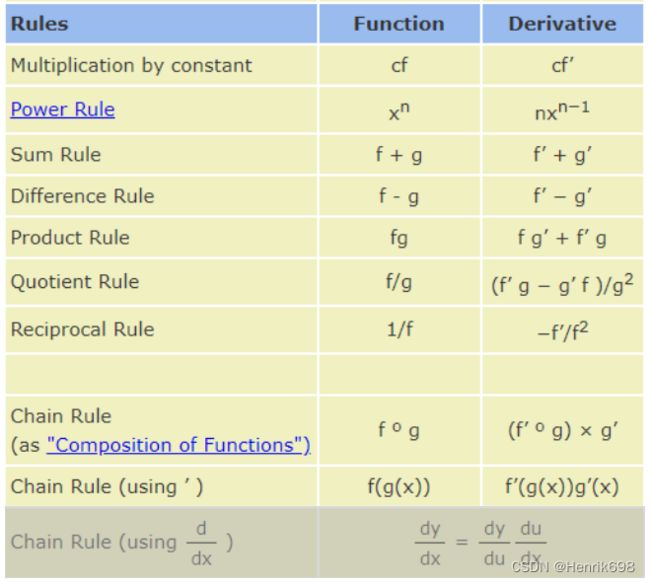
chain rule：dy/dx = (dy/du) * (du/dx)
可以发现链式法则，是y对中间变量u求导再乘以中间变量u对x的求导。

基础规则 Basic Rule

▪ + 加法的求导规则

▪ − 减法的求导规则

▪ ()′ = ′ + ′ 乘法的求导规则

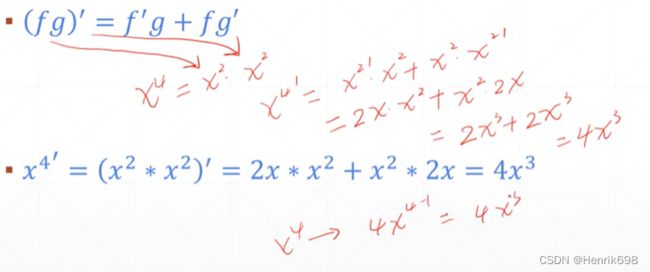
▪ / = ( ′ + ′ ) / ² 除法的求导规则
例子：softmax激活函数，这里p就是概率的意思，p所对应的函数就是softmax激活函数。

▪ Chain rule 链式规则的求导规则：y / x = (y / u) × (u / x)
y到x的过程中，中间经历一个中间变量u后，到达x。
在实际中 x输入层加上激活函数，通过hidden layer层u后，到达y预测结果。
例如：两个线性层相加
y₁ = xw₁ + b₁
y₂ = y₁w₂ + b₂ = (xw₁ + b₁)w₂ + b₂
将y₁看做为中间变量：
y₂ / w₁ = (y₁w₂ + b₂) / w₁ = ((y₁w₂ + b₂) / y₁) × (y₁ / w₁)
将y₁视作为一个整体的值：
y₂ / w₁ = w₂ × ((xw₁ + b₁) / w₁) = w₂ × x
因此：
y₂ / w₁ = w₂ × x
对于一个比较简单的线性层，可以直接展开得到。
但是对于实际的神经网络，还有一个激活函数，如果加一个激活函数后展开会非常复杂了，不能很好的一次到位。运用链式法则可以让神经网络变得简洁。

Chain rule 链式法则

针对神经网络的具体例子：
对中间值的求导，将一个较为复杂的偏微分的式子通过中间值简化了。

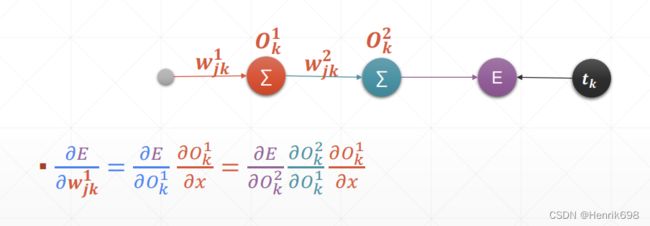
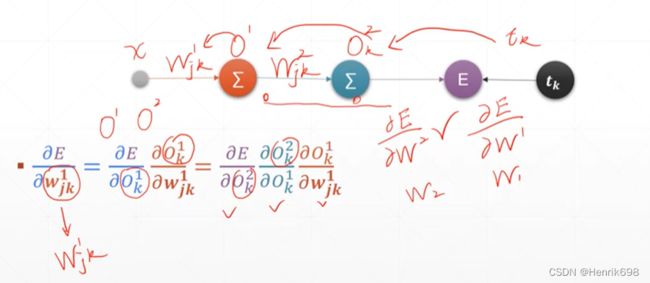
pytorch进行链式法则的计算

pytorch实现上图的计算：

import torch
from torch.nn import functional as F

x = torch.tensor(1.)
w1 = torch.tensor(2.,requires_grad=True)
b1 = torch.tensor(1.)
w2 = torch.tensor(2.,requires_grad=True)
b2 = torch.tensor(1.)

y1 = x*w1 + b1
y2 = y1*w2 + b2

#torch.autograd.grad()返回的是元组(tensor(2.),)，应将数据类型变为tensor(), 使用output[0]输出即可
print(torch.autograd.grad(y2,[y1],retain_graph=True))
#这里dy2_dy1 = w2
dy2_dy1 = torch.autograd.grad(y2,[y1],retain_graph=True)[0]
print('dy2_dy1:',dy2_dy1)

#这里dy1_dw1 = x
dy1_dw1 = torch.autograd.grad(y1,[w1],retain_graph=True)[0]
print('dy1_dw1:',dy1_dw1)

#链式法则求dy2_dw1:
print('链式法则dy2_dy1*dy1_dw1:',dy2_dy1 * dy1_dw1)

#直接求导dy2_dw1
dy2_dw1 = torch.autograd.grad(y2,[w1],retain_graph=True)[0]
print('直接求导dy2_dw1:',dy2_dw1)

#发现直接求导dy2_dw1与链式法则dy2_dy1*dy1_dw1结果是相同的。

下节，将会使用链式法则，推导一个完整的全连接层的梯度传播的过程。

八、MLP(Multilayer Perceptron多层感知机) 反向传播推导

本节会完整介绍与实际使用一模一样的多层感知机的反向传播方式。

本节公式会稍微多一些，这章节是deep learning最后的一些公式，这些掌握了后，对于后面的章节的内容学起来会非常的快。

回顾一下链式法则：

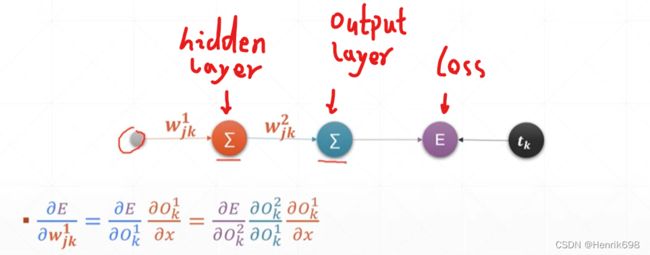
回顾一下只有一层输入节点的多输出感知机的链式推导公式：Multi-output Perceptron

多层感知机MLP(Multi-Layer Perceptron)

多层感知机意味着，输出层前会有多个输入层，且每个输入层都是由输出节点输出的内容作为输入的节点的。

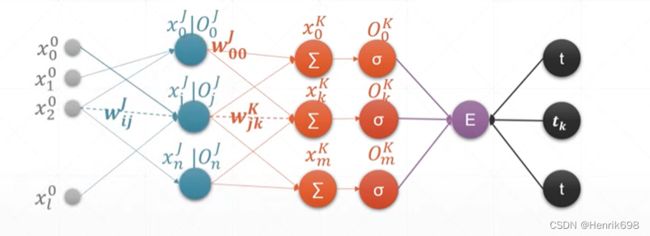
图中，Oⱼᴶ 相当于xⱼ⁰，就是输入层的最后一个输出，是隐藏层中经过激活函数后的输出内容。

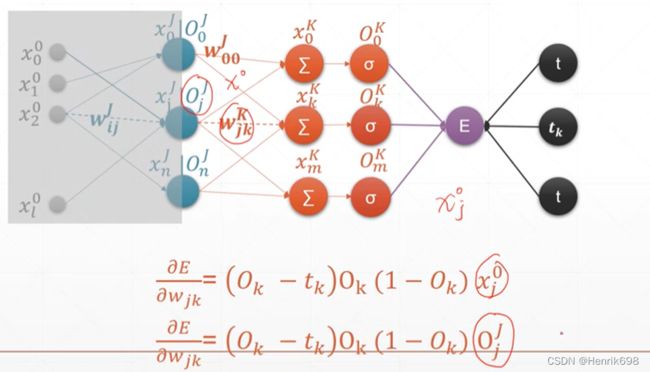
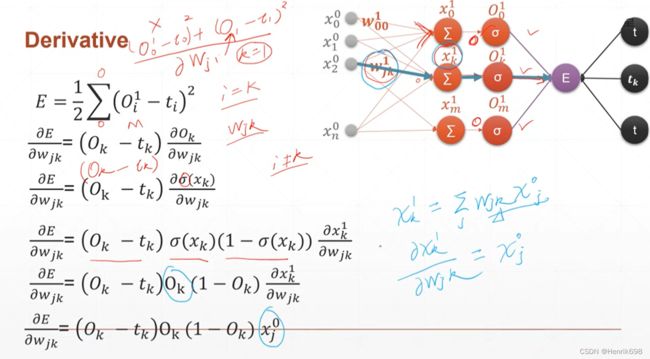
推导最终Loss与最初wᵢⱼ的梯度（E / wᵢⱼ）:

其中：
E / wⱼₖᴷ = (Oₖᴷ - tₖ)Oₖᴷ(1-Oₖᴷ)Oⱼᴶ
(Oⱼᴶ = xⱼᴶ经过激活函数处理后的结果)
(Oₖᴷ - tₖ)Oₖᴷ(1-Oₖᴷ) 这部分是知道的用δₖᴷ表示，δₖᴷ是一个小k行1列的矩阵，中间层有多少个输出节点，δ矩阵就有多少个元素，小k为元素个数，大K表示的是第K层。
E / wⱼₖᴷ = δₖᴷ Oⱼᴶ
Oⱼᴶ为上一层的输出节点。

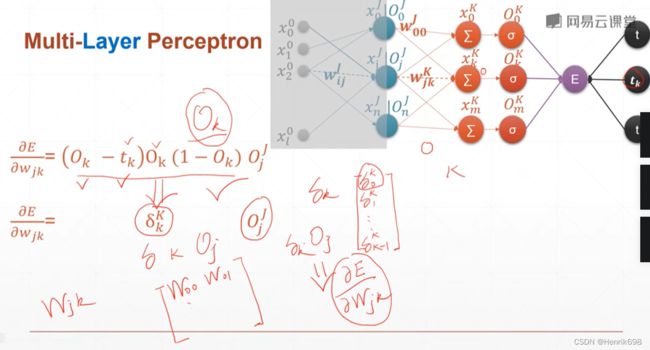
通过这种组合可以得到一个梯度矩阵
W₀₀ W₀₁ … W₀ₖ
W₁₀ W₁₁ … W₁ₖ
…
…
其中每个元素Wⱼₖ，就表示K层的梯度（Oₖᴷ / wⱼₖᴷ），即 (Oₖᴷ - tₖ)Oₖᴷ(1-Oₖᴷ) Oⱼᴶ，其实就是红色圈中的内容所涉及的梯度，即该K层jk链路的梯度 (j对应上一层的输出节点Oⱼᴶ，k对应K层说对应的输出链路)，这里的W元素时一个单层感知机。
例如，W₀₀ 表示第1层第1条链路的偏微分。


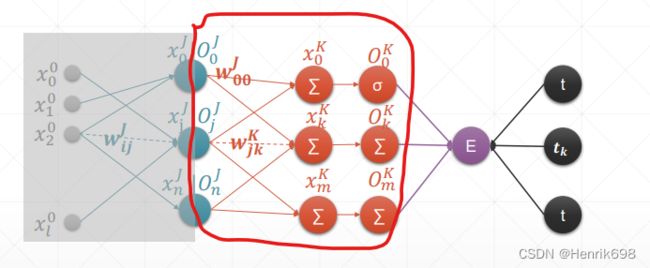
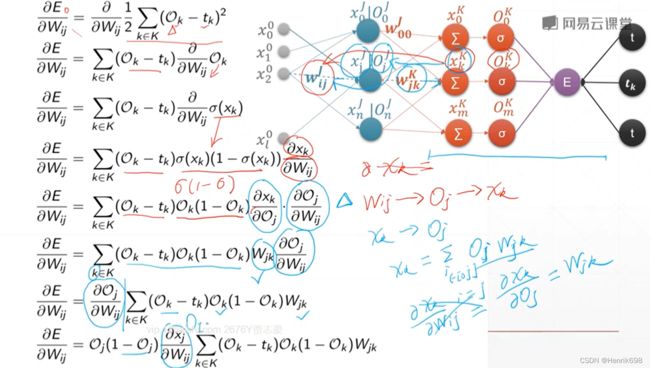
最终通过链式法则求出：E / wᵢⱼᴶ = Oⱼᴶ / wᵢⱼᴶ * E / Oⱼᴶ

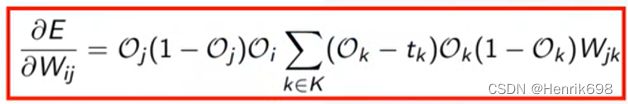
可以注意到的是E / wᵢⱼᴶ 与x₂⁰，Oⱼᴶ，以及所有的K层δₖᴷ和wⱼₖᴷ都有关系，δₖᴷ = (Oₖᴷ - tₖ)Oₖᴷ(1-Oₖᴷ) 。

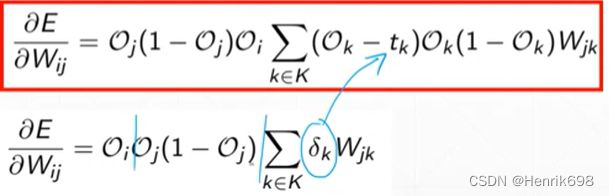
最终获得 E / wᵢⱼᴶ = Oⱼ δⱼ
其中 δⱼ = Oⱼ(1-Oⱼ) Σδₖwⱼₖ ，这里k∈K。

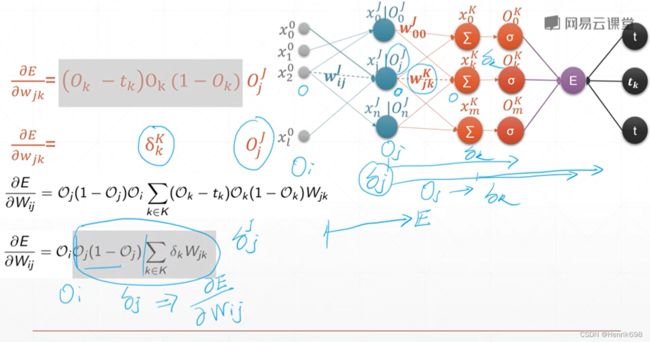
总结Loss与最初wᵢⱼ的梯度（E / wᵢⱼ）

对于一个输出层节点 k∈K
E / wⱼₖ = Oⱼ δₖ
where:
δₖ = Oₖ(1-Oₖ)(Oₖ-tₖ)

对于一个隐藏层节点 j∈J
E / wᵢⱼ = Oⱼ δⱼ
where:
δⱼ = Oⱼ(1-Oⱼ) Σδₖwⱼₖ (k∈K)


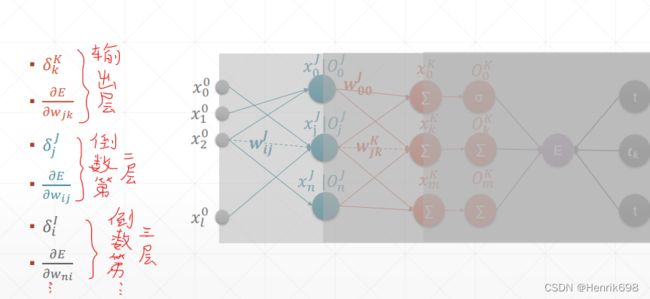
通过这种不停的迭代，计算出前面所有层的偏微分信息，得到了偏微分信息以后，就可以直接使用链式法则（梯度更新方式），对权值不断的更新，直到权值达到我们想要的程度。
这一些列过程其实就是函数优化的问题。

九、2D函数优化实例

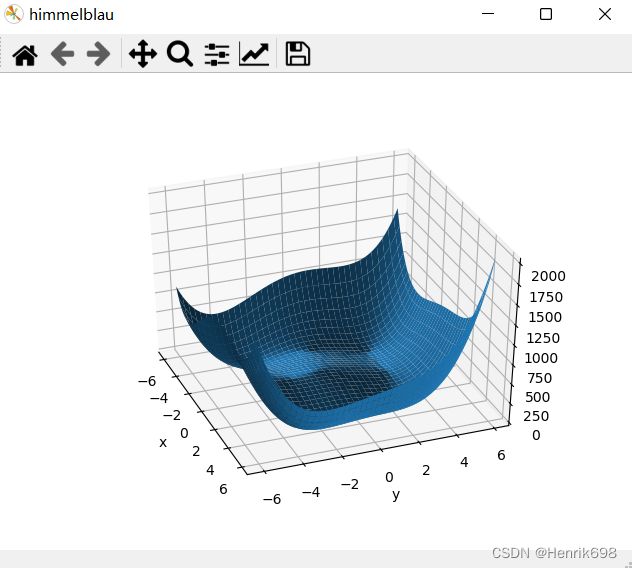
Himmelblau函数

f(x,y)= (x² + y - 11)² + (x + y² - 7)²
这个函数有两个自变量x和y。这个函数类似一个碗，底部有四个局部最小值，这四个局部最小解都是0，也都是全局最小解。

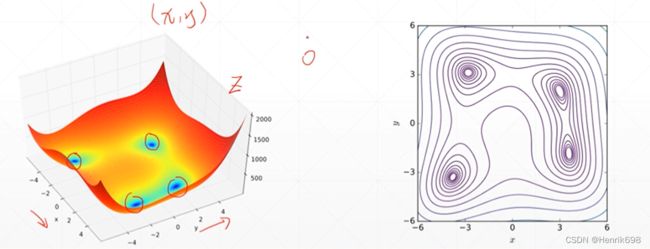
梯度下降求解最小值 对Himmelblau函数

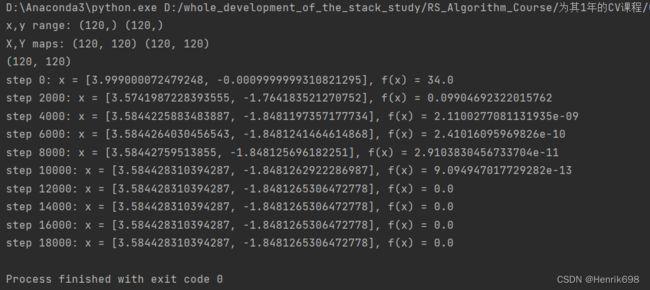
通过对这个函数设计的梯度下降法则能不能很好找到最小值，找到的这个解与真实的结果进行对比，以查看其学习效果的好坏：

绘制曲线：

import matplotlib.pyplot as plt
import numpy as np
import torch
from torch.nn import functional as F
from mpl_toolkits.mplot3d import axes3d

def himmelblau(x):
    return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2

x = np.arange(-6, 6, 0.1) #120个点
y = np.arange(-6, 6, 0.1)
print('x,y range:', x.shape, y.shape)
X,Y = np.meshgrid(x,y)
#meshgrid(x,y):
#横坐标的矩阵，与纵坐标的矩阵，组合起来就形成了网络，其网络上的每一个点(x,y)组合起来的。
#X是120列从-6到6的步长为0.1的120个值，向下重复120遍组成120行。
#Y是120行从-6到6的步长为0.1的120个值，向右重复120遍组成120列。
#每个交汇处的坐标就是有X和Y组成的
#就相当于形成两张图片，一张图片上的点，和另一张图片相同位置的点拼在一起，就形成了该点的坐标(X[index1],Y[index1]),一共有120*120个这样的点，这个点存储着横坐标和纵坐标。
#将这个坐标X,Y，送入函数中，求得Z,这个Z就是对应某一个点(X,Y)的Z值。
#进一步了解meshgrid()，可以查看https://blog.csdn.net/lllxxq141592654/article/details/81532855

print('X,Y maps:',X.shape, Y.shape)
Z = himmelblau([X,Y])
print(Z.shape)

fig = plt.figure('himmelblau')
ax = fig.gca(projection ='3d')
ax.plot_surface(X,Y,Z)
ax.view_init(60, -30)
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()

使用随机梯度下降的方法求解一下最小值：

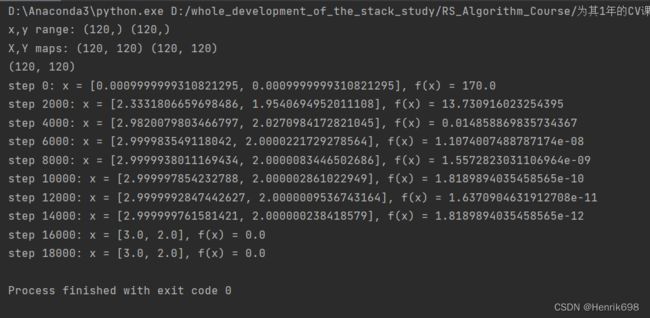
这里初始的位置是（0,0）

import matplotlib.pyplot as plt
import numpy as np
import torch
from torch.nn import functional as F
from mpl_toolkits.mplot3d import axes3d

def himmelblau(x):
    return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2

x = np.arange(-6, 6, 0.1) #120个点
y = np.arange(-6, 6, 0.1)
print('x,y range:', x.shape, y.shape)
X,Y = np.meshgrid(x,y)
#meshgrid(x,y):
#横坐标的矩阵，与纵坐标的矩阵，组合起来就形成了网络，其网络上的每一个点(x,y)组合起来的。
#X是120列从-6到6的步长为0.1的120个值，向下重复120遍组成120行。
#Y是120行从-6到6的步长为0.1的120个值，向右重复120遍组成120列。
#每个交汇处的坐标就是有X和Y组成的
#就相当于形成两张图片，一张图片上的点，和另一张图片相同位置的点拼在一起，就形成了该点的坐标(X[index1],Y[index1]),一共有120*120个这样的点，这个点存储着横坐标和纵坐标。
#将这个坐标X,Y，送入函数中，求得Z,这个Z就是对应某一个点(X,Y)的Z值。

print('X,Y maps:',X.shape, Y.shape)
Z = himmelblau([X,Y])
print(Z.shape)

fig = plt.figure('himmelblau')
ax = fig.gca(projection ='3d')
ax.plot_surface(X,Y,Z)
ax.view_init(60, -30)
ax.set_xlabel('x')
ax.set_ylabel('y')
# plt.show()

x = torch.tensor([0.,0.],requires_grad=True)
#要来优化目标x，这个x是传入himmelblau函数中的参数x,所以需要梯度信息
#这里要计算Pred/x，优化预测值Pred，优化目标是x，这个x就是(x,y)。

#使用一个优化器，优化器的目标就是x,学习率learning rate就是0.001
#只要得到梯度以后，下面这就话就可以自动完成x' = x - 0.001*▽x 和 y' = y - 0.001*▽y
#之后只要调用optimizer.step()就会更新一次x'和y'。
optimizer = torch.optim.Adam([x],lr=1e-3)

for step in range(20000):

    pred = himmelblau(x) #将x送进函数中，得到预测值。

    optimizer.zero_grad() #这里是直接将梯度信息清零
    pred.backward() #回退，获得梯度值
    optimizer.step() #将x和y更新为x'和y'

    if step % 2000 == 0:
        print('step {}: x = {}, f(x) = {}'
              .format(step,x.tolist(),pred.item())) #这里.item()的说明可以查看：https://blog.csdn.net/weixin_45092662/article/details/113768531

如果将初始位置更改为（4,0）查找的最小值会改变：

import matplotlib.pyplot as plt
import numpy as np
import torch
from torch.nn import functional as F
from mpl_toolkits.mplot3d import axes3d

def himmelblau(x):
    return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2

x = np.arange(-6, 6, 0.1) #120个点
y = np.arange(-6, 6, 0.1)
print('x,y range:', x.shape, y.shape)
X,Y = np.meshgrid(x,y)
#meshgrid(x,y):
#横坐标的矩阵，与纵坐标的矩阵，组合起来就形成了网络，其网络上的每一个点(x,y)组合起来的。
#X是120列从-6到6的步长为0.1的120个值，向下重复120遍组成120行。
#Y是120行从-6到6的步长为0.1的120个值，向右重复120遍组成120列。
#每个交汇处的坐标就是有X和Y组成的
#就相当于形成两张图片，一张图片上的点，和另一张图片相同位置的点拼在一起，就形成了该点的坐标(X[index1],Y[index1]),一共有120*120个这样的点，这个点存储着横坐标和纵坐标。
#将这个坐标X,Y，送入函数中，求得Z,这个Z就是对应某一个点(X,Y)的Z值。

print('X,Y maps:',X.shape, Y.shape)
Z = himmelblau([X,Y])
print(Z.shape)

fig = plt.figure('himmelblau')
ax = fig.gca(projection ='3d')
ax.plot_surface(X,Y,Z)
ax.view_init(60, -30)
ax.set_xlabel('x')
ax.set_ylabel('y')
# plt.show()

x = torch.tensor([4.,0.],requires_grad=True)
#要来优化目标x，这个x是传入himmelblau函数中的参数x,所以需要梯度信息
#这里要计算Pred/x，优化预测值Pred，优化目标是x，这个x就是(x,y)。

#使用一个优化器，优化器的目标就是x,学习率learning rate就是0.001
#只要得到梯度以后，下面这就话就可以自动完成x' = x - 0.001*▽x 和 y' = y - 0.001*▽y
#之后只要调用optimizer.step()就会更新一次x'和y'。
optimizer = torch.optim.Adam([x],lr=1e-3)

for step in range(20000):

    pred = himmelblau(x) #将x送进函数中，得到预测值。

    optimizer.zero_grad() #这里是直接将梯度信息清零
    pred.backward() #回退，获得梯度值
    optimizer.step() #将x和y更新为x'和y'

    if step % 2000 == 0:
        print('step {}: x = {}, f(x) = {}'
              .format(step,x.tolist(),pred.item())) #这里.item()的说明可以查看：https://blog.csdn.net/weixin_45092662/article/details/113768531

通过改变不同个初始位置，可以发现找到最小值的速度是不一样的，所以在选取初始位置时需要慎重。