弱监督、具有可解释性的应用题解答

点击蓝字

关注我们

AI TIME欢迎每一位AI爱好者的加入！

Previous neural solvers of math word problems (MWPs) are learned with full supervision and fail to generate diverse solutions. In this paper, we address this issue by introducing a weakly-supervised paradigm for learning MWPs. Our method only requires the annotations of the final answers and can generate various solutions for a single problem. To boost weakly-supervised learning, we propose a novel learning-by-fixing (LBF) framework, which corrects the misperceptions of the neural network via symbolic reasoning. Specifically, for an incorrect solution tree generated by the neural network, the fixing mechanism propagates the error from the root node to the leaf nodes and infers the most probable fix that can be executed to get the desired answer. To generate more diverse solutions, tree regularization is applied to guide the efficient shrinkage and exploration of the solution space, and a memory buffer is designed to track and save the discovered various fixes for each problem.

 

Previous neural solvers of math word problems directly translate problem texts into equations, lacking an explicit interpretation of the situations, and often fail to handle more sophisticated situations. To address such limits of neural solvers, we introduce the concept of a situation model, which originates from psychology studies to represent the mental states of humans in problem-solving, and propose SMART, which adopts attributed grammar as the representation of situation models for algebra story problems. Specifically, we first train an information extraction module to extract nodes, attributes, and relations from problem texts and then generate a parse graph based on a pre-defined attributed grammar. An iterative learning strategy is also proposed to improve the performance of SMART further.

洪逸宁：加州大学洛杉矶分校一年级博士生，方向为计算机视觉、自然语言处理，师从朱松纯教授。在ECCV、ICML、AAAI等会议中发表文章。

一、Learning by Fixing: Solving Math Word Problems with Weak Supervision

今次的分享包括两篇AI解数学题的论文，均发表在AAAI2021上面。第一篇论文采用弱监督的方法解数学题。

研究人员一般用neural symbolic 模型来解数学题，这种方法首先将题目通过sequence to tree或者sequence two sequence的神经网络模型学得数学关系，然后利用模型生成关系之间的表达式。最后数学表达式通过symbolic execution得到答案。

在此之前的方法主要以fully supervise为主，这种方法的主要特点是数学表达式需要有提前的标注，而模型的训练则是有这些被标注的数学表达式完成的，并且优化expression accuracy。但是当测试时，则还需要经过symbolic模型和神经网络模型，而evaluate是以answer accuracy进行判断的，这就导致了与训练时的模型标准不一样，导致结果产生分歧。

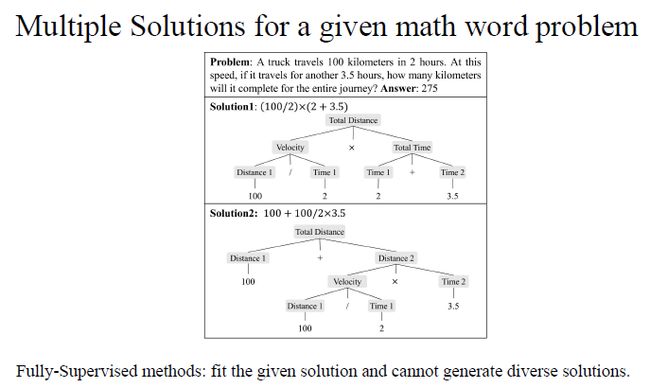
Fully-supervised 方法还面临着另一个问题，，即一个数学题也可能不止一种解法。例如上图中的题目可以从先计算速度，再进行速度乘以时间计算总路程入手，也可以从分段计算路程的角度入手。但是对于Fully-supervised method来说，模型的解题思路只局限于一种解法，而忽略了解法的多样性。

Fully-supervised方法的另一个问题则是需要通过大量有标注的数据进行训练，但是数学题和最终答案获取是相对比较容易的，但是标注则是一个比较困难的工程。所以我们希望通过一个弱监督的方法避免对数学表达式的依赖，从而方便的通过数学题和最终答案获得解题的AI模型。

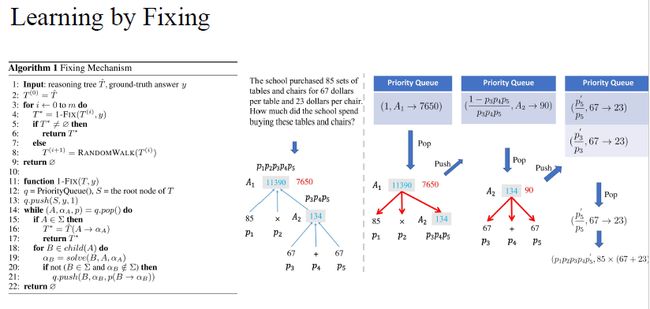
基于以上理念，我们提出了弱监督的学习方法。其首先通过神经网络生成数学表达式，但是在没有标注的情况下，不会去训练模型。然后通过symbolic execution模型计算出数学表达式的最终答案，并且这个答案是与标准答案的有所差别的。为了获得标准的答案，就需要通过top down的方式从上往下的一一对比正确答案，例如图中节点2改为3.5，获得了正确的表达式。除此之外神经网络模型还会组合出不同的表达式，那么对这些表达式进行修改就可以获得正确的数学表达式，进一步的用这些正确的数学表达式去训练神经网络模型。

上图显示了模型的整体框架，可以看到在神经模型中使用了goal-driven tree 模型去生成数学表达式，而这个表达式就是修改的基础，并且修改过后的正确表达式会放入buffer中，而buffer中存储的表达式就是训练tree模型。

goal-driven tree structured 模型主要运行方式是通过一个GRU生成q0，之后以分解tree的方式不断的分解q0，使之生成基本的数学表达式。

但是生成的数学表达式不能保证正确率，因此我们提出了一个基于我们另一篇ICM论文的fixing框架，这是一个以top down方式修改数学表达式的框架。

至此，我们提出了learning by fixing流程。我们把所有可能的修改放到priority queue中，通过从priority queue中的内容去修改expression tree。然后我们还提出了one step fix去修改数学表达式。并且还可以通过multi step的方法，在修改tree不成功的时候通过random walk去修改其中一个node，然后再尝试去修改。

通过限制神经网络模型的数学表达式的程度避免出现无限长的tree，所以我们提出tree regularization方法去限制tree的大小，让它不能生成任意程度的数学表达式。

同时我们提出memory buffer，当一个数学题有不同的解法时，把这些解法放入buffer中，然后用buffer中所有的tree去训练神经网络模型。

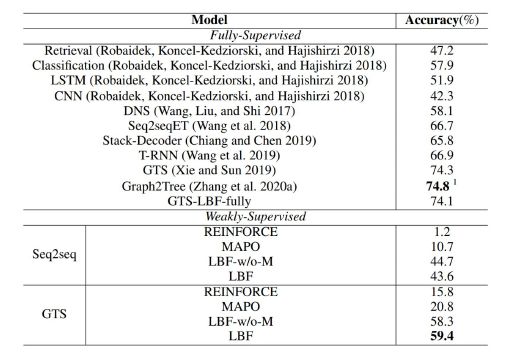
实验使用的数据集为math23k。我们通过评价top 1/3/5的预测准确率去检测模型能否学得多样化的解法。在神经网络模型方面选取了 sequence to sequence做 baseline，和goal-driven tree-structured 模型。在learning方面，同时比较了learning by fixing框架和REINFORCE框架和MAPO框架，其中MAPO在semantic parsing中表现出了state of the art的准确率。除此之外，我们还测试了memory buffer在learning by fixing中承担的作用。

可以看到在弱监督方面，我们的模型性能远远高于baseline模型。

在前3个的表达式准确率和前5个表达式准确率中有memory buffer的模型高于没有memory buffer的模型。同时我们还做了ablative study，去检测fixing修改过程需要的步骤，可以看到最多只需要50步，可以达到比较好的效果。

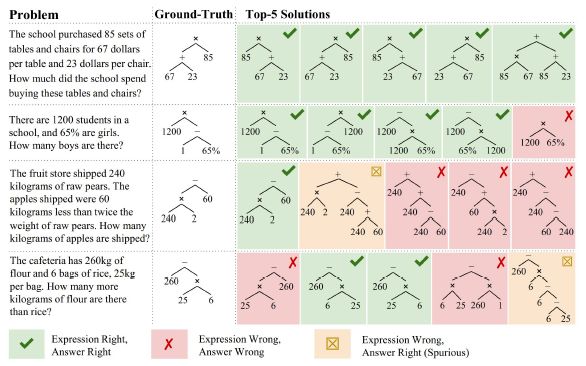
观察模型的qualitative study，可以看出我们的模型可以实现多样化解法。同时会产生似是而非的写法，即结论正确，但过程没有意义。

• 我们提出了应用于数学题上的弱监督框架，并且提出了learning by fixing框架去增强学习能力。

• 在future work上面我们去解决生成结果包含似是而非的解。

• 同时我们觉得一个弱监督的，大规模的数学题解是非常有必要的。

二、SMART : A Situation Model for Algebra Story Problems via Attributed Grammar

第二篇paper希望通过具有可解释性的方法，把数学题的解题过程展现出来，类似于数学老师教学生写数学题，把每一步的步骤都写出来。并且我们用Song-Chun Zhu老师提出的attributed grammar作为解决思路。数学题主要分为数字题、几何题、概念题、符号题，还有应用题。

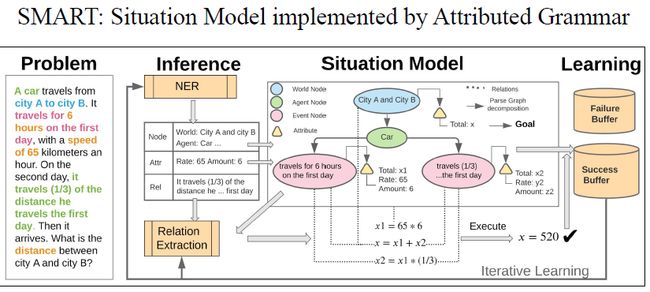
上图是一个应用题案例，一个车从a城到b城，它有速度和行驶时间，然后求a城和b城之间的距离。应用题是一类特殊的数学题，它描述了一个现实生活中的场景，提出了在场景中的一个未知变量，并且题目中具有故事纲要，其中包含了characters，objects和actions，这些都在心理学或认知科学的论文中有所定义。

现有的方法主要使用神经网络模型来解答数学题，但是这样的模型缺少泛化能力，因为模型训练时会使用一些比较简单的数据，但是测试时会面临更复杂的题目，这往往会导致神经网络模型不能正常工作。比如说在第一道题的中只问两天，神经网络模型见过这样数据可以很快的解出来。可是第二题询问三天，使得问题更复杂，因为神经网络模型没有见过这样的数据，所以没有解题能力。

另外一个问题是神经网络模型缺乏可解释性，这里是一个标注好的数学表达式，其计算形式即便对人类而言也是不容易理解的，并且仅从表达式来看不知道表达的内容，所以这样的表达式很难被神经网络模型学习到，并且不能把中间的解题过程比较好的展示出来。

所以为了解决上面的问题，我们首先提出了一个数据集，应用题6.6K。这个数据集包含4种类型的应用题，分别是行程题，价格题，关系题，还有任务完成题。

我们提出了一个重要的概念，situation模型。Situation模型是在心理学和认知科学中被广泛用来进行题目解答的模型，用来represent agent actions and events。这是一个应用于人类解题心理过程的模型，同时也是一个场景模型。根据之前的认知科学理论，人类的解数学能力，比如数学能力和逻辑能力是作用于situation 模型中，而不是像神经网络一样直接作用于文字。我们的situation 模型和一个数学概念模型进行交互，数学概念模型把一些运算关系进一步嵌入到场景模型中。这两个mode之间的交互，完成了解题过程。

这是我们提出的situation 模型。其通过attributed grammar，也就是有特征的grammar实现。首先一个问题通过graph的形式转换成situation 模型，situation 模型中包含world node，用于限制数学题的范围。然后agent node统计有多少个物体在这个数学题中，event node统计这些物体分别做了哪些行为。这些node包含有一些特征，例如这道题中是距离、时间和速度，并且这些特征之间会有一些关系，例如距离等于时间乘以速度。所以为了得到graph，我们首先通过一个命令实体识别提取题目的点和特征，特征之间的关系是通过relational extraction模块中的sequence to sequence来完成的。通过这个模块把表达关系文字和特征转变成方程，然后解方程就能得到最终答案。如果答案是正确的就放到success buffer中，不然就放到failure buffer中。然后用success buffer的例子进一步训练命名实体识别和关系表达，所以这其实是iterative learning过程，之后再进一步的优化failure buffer。

Attributed grammar定义了graph的parse过程和production rules。其包含有5个部分：star symbol，一些nodes包含有world agent和event，attribute包含有速度，amount，数量之类，E表示关系，即在attributed上的方程，production rules是graph的分解原理。我们希望能找到一个概率最大的parse graph。

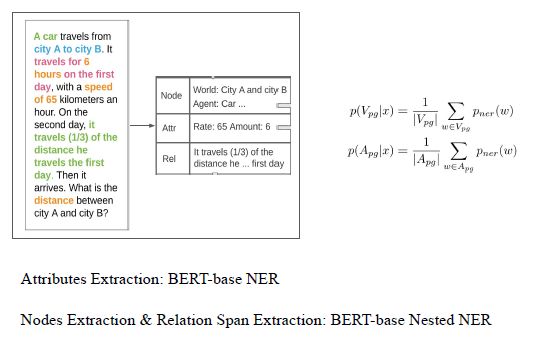
所以我们有一个grammar parsing过程。首先过一个NER。而parse graph由三个概率组成，第一部分是点，第二部分是attribute，第三部分是关系。

通过命名实体表达，就可以找到点的概率和关系的概率。

通过sequence to sequence可以将关系转换成方程。

由于我们的框架是一个没有标注的self supervision框架，所以我们提出rule-based initial parser去获得最初的supervision，进而训练框架。

具体而言，首先通过attribute extraction的关系提取出题目中的一些速率或者是个数等数字，然后利用单位确定关系。此外还可以通过 Dependency Parsing, Pos Tagging and Regular Expressions这些方法提取点信息。

Relational extraction则是通过first order logic获得，即我们定义了一些functions和 predicate，然后到题目中寻找匹配项。

而解题过程则是通过寻找题目中的目的，通过命名实体识别寻找题目中询问相关的词汇，获得目的，最后通过SymPy这个工具写出解题过程。

在iterative learning框架中，通过propose一些parse graph，检测是否能够successfully execute to the right answer，如果可以就将其放入success buffer中，否则放到failure buffer中。然后进行iterative learning过程，通过framework如果是正确的就把它放入success buffer，否则放入failure buff。

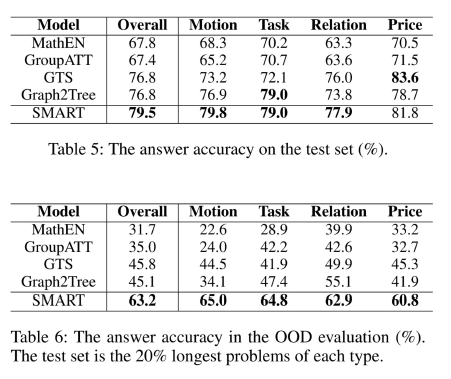
实验采用应用题6.6K作为数据集，然后我们选用了一些baseline 模型，主要为神经网络。

从实验结果可以看出，我们的模型性能要高于其他的神经网络模型。我们还做了OOD实验，out of distribution，用于检测模型对于未见过的题目能达到多高的准确率，可以看到我们的模型对于这项检测表现出了较好的效果，具有较高的泛化能力。

然后进行qualitative study，可以看到在比较简单的问题上面，因为模型在训练中有过类似的题目，神经网络模型和我们的模型都可以得到比较好的效果。但是在第3个、第4个这类比较复杂的问题上，神经网络模型表现的缺乏泛化能力，而我们的模型因为具有可解释性，可分解的能力，所以依然可以达到很好的效果。

• 我们把应用题和其他类型的数学题做了区分，并且表明应用题应该被单独研究。

• 我们介绍了心理学中的situation 模型，并且提出了相应的AI模型，based on attributed grammar。然后在attributed grammar中实现situation 模型。

• 我们的模型可以达到更好的可解释性，还有泛化能力。

相关资料

论文标题：

1、"Learning by Fixing: Solving Math Word Problems with Weak Supervision"

2、"SMART: A Situation model for Algebra Story Problems via Attributed Grammar"

论文链接：

https://arxiv.org/pdf/2012.10582.pdf

https://arxiv.org/pdf/2012.14011.pdf

整理：闫   昊

审稿：洪逸宁

排版：岳白雪

AI TIME欢迎AI领域学者投稿，期待大家剖析学科历史发展和前沿技术。针对热门话题，我们将邀请专家一起论道。同时，我们也长期招募优质的撰稿人，顶级的平台需要顶级的你！

请将简历等信息发至[email protected]！

微信联系:AITIME_HY

AI TIME是清华大学计算机系一群关注人工智能发展，并有思想情怀的青年学者们创办的圈子,旨在发扬科学思辨精神，邀请各界人士对人工智能理论、算法、场景、应用的本质问题进行探索，加强思想碰撞，打造一个知识分享的聚集地。

更多资讯请扫码关注

 

（直播回放：https://www.bilibili.com/video/BV1pp4y1h7H9?share_source=copy_web）

（点击“阅读原文”下载本次报告ppt）