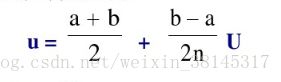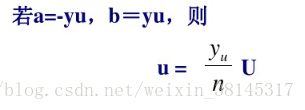模糊控制详解
描述输入和输出变量的词集
在模糊控制中,输入输出变量大小是以语言形式描述的,一般都选用大中小三个词汇来描述模糊控制器的输入,输出变量的状态,再加上正负两个方向和零状态,共有7个词汇:
{负大,负中,负小,零,正小,正中,正大}
一般用这些词的英文字头缩写为:
{NB,NM,NS,O,PS,PM,PB}
为了提高系统稳态精度,通常在误差接近于零时增加分辨率,将零又分为整零和负零,因此,描述误差变量的刺集一般取为:
{负大,负中,负小,负零,正零,正小,正中,正大}
用英文字头简记为:
{NB,NM,NS,NO,PO,PS,PM,PB}
注意,上述零,负零,正零和其他词汇一样,都是描述了变量的一个区域。
变量的模糊化
某个变量变化的实际范围称为该变量的基本论域。记误差的基本论域为【-xe,xe],误差变化的基本论域为[-xc,xc]
模糊控制器的输出变量(系统的控制量)的基本论域为【-yu,yu]
基本论域内的量是精确量,因而模糊控制器的输入和输出都是精确量,但是模糊控制算法需要模糊量。因此输入的精确量(数字量)需要转换为模糊量,这个过程称为“模糊化”。
另一方面,模糊算法所得到的模糊控制量需要转换为精确的控制量,这个过程称为清晰化或者反模糊化。即取变量的模糊子集论域为
{-n, -n+1,…0,…,n-1,n}
从基本论域[a,b]到模糊子集论域【-n,n]的转换公式为
一般选择模糊论域中所含元素个数为模糊语言词集总数的二倍以上,确保模糊集能较好的覆盖论域,避免出现失控现象,
隶属度
为了实现模糊化,要在上述离散化了的精确量与表示模糊语言的模糊量之间建立关系,即确定论域中的每个元素对于各个模糊语言变量的隶属度。
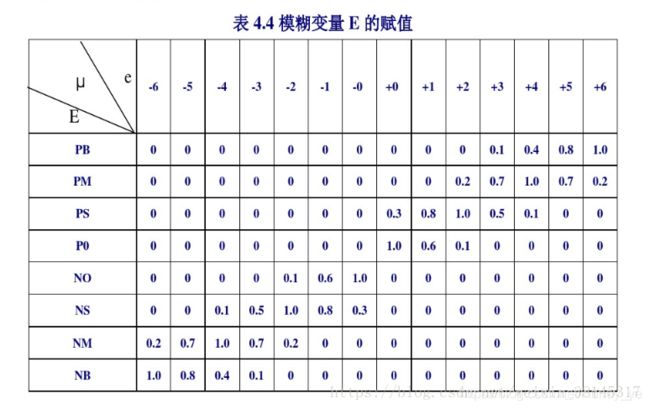
隶属度是描述某个确定量隶属于某个模糊语言变量的程度。常用的确定模糊变量隶属度的赋值表见下表
建立模糊控制规则
下面推荐一种根据系统输出的误差及误差的变化趋势,消除误差的模糊控制规则,该规则用下述21条模糊条件语句来描述,基本总结了众多的被控对象手动操作过程,各种可能出现的情况和相应的控制策略。
上述的21条模糊条件语句可以归纳为模糊控制规则表
模糊关系与模糊推理
模糊控制规则实际上是一组多重条件语句,可以表示为从误差论域到控制量论域的模糊关系矩阵R,通过误差的模糊向量E和误差变化的模糊向量EC与模糊关系R的合成进行模糊推理,得到控制量的模糊向量,然后采用清晰化方法将模糊控制向量转换为精确量。
根据模糊集合和模糊关系理论,对于不同类型的模糊规则可用不同的模糊推理方法,下面以常用的if A then B类型的模糊规则的推理为例,若已知输入为A,则输出为B,若现在已知输入为A’,则输出B’用合成规则求取
B’=A’OR
由于系统的控制规则库是由若干条规则组成的,对于每一条推理规则都可以得到一个相应的模糊关系,n条规则就有n个模糊关系,R1,R2,…,Rn,对于整个系统的全部控制规则所对应的模糊关系及可对n个模糊关系Ri(i=1,2,…n)取并操作得到
模糊控制向量的模糊判决-清晰化
重心法(普通加权平均法)
例如 u’=0.1/2+0.8/3+1.0/4+0.1/6
则 u=(20.1+30.8+41+50.8+6*0.1)/0.1+0.8+1.0+0.8+0.1=4
模糊控制表
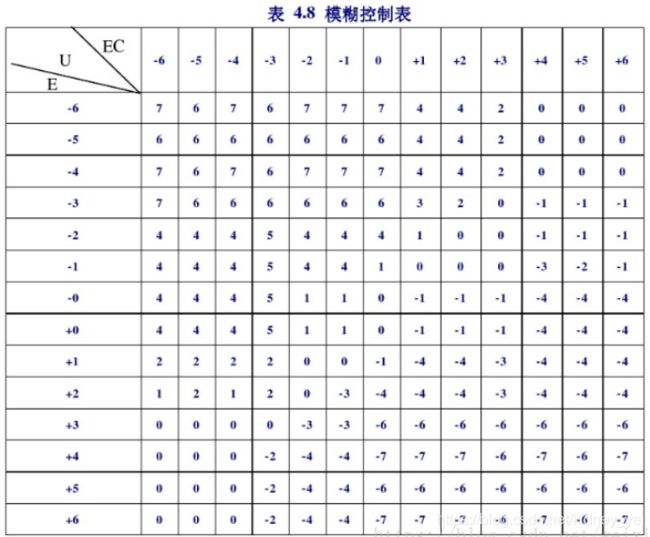
模糊关系,模糊推理以及模糊判决的运算可以离线进行,最后得到模糊控制输入量的量化等级E,EC与输出量即系统控制量的量化等级U之间的确定关系,这种关系通常称为控制表,对英于前面的21条控制规则的控制表如下表所示
确定实际的控制量
显然,实际的控制量u应为从控制表中查到的量化等级u乘以比例因子,设实际的控制量u的变化范围为[a,b],量化等级为(-n,-n+1,…o,.n-1,n),则实际的控制量应为
转载至CSDN博主:wanghua609,
(https://blog.csdn.net/weixin_38145317/article/details/82966901).