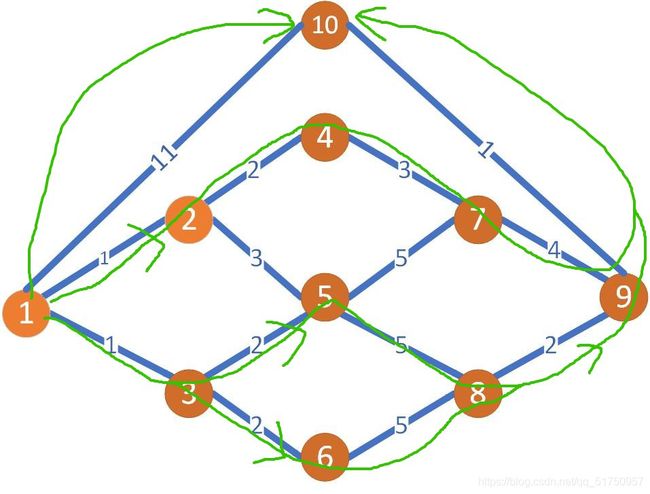
Floyd 算法，找出所有最短路径或最长路径 matlab （二）

所有最短路径

在（一）中，我们获得了距离矩阵和路由矩阵（元胞）
这个一个无向图

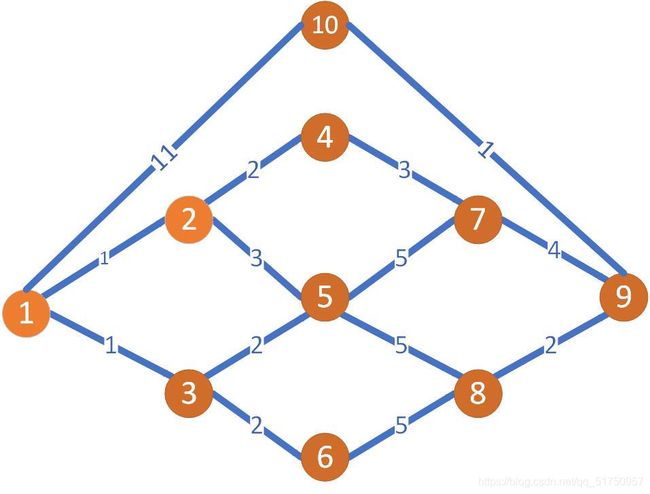
这是上次算出的距离矩阵和路由矩阵，


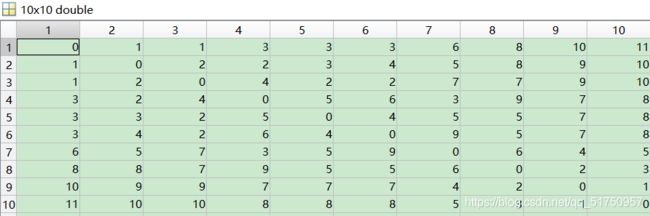
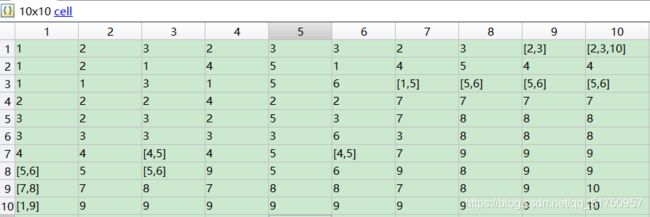
接下来介绍如何根据这个路由矩阵（元胞）列出所有最短路径，结果存储在一个矩阵里，每一行代表一条最短路径的标号。
定义列出所有最短路径的函数，原理是经过一次次迭代，不断把当前路径增长且数目变多，直至结果稳定。
基本思想：用和原始Floyd算法同样的方法，在路由矩阵上进行寻路。如果遇到所取的元素是一个列表，则遍历列表中的a个元素，生成a条最短路径，再分别往下走，再遇到列表，则遍历列表中的b个元素，得到b * a条最短路径，再分别往下走，以此类推，直到到达目标点，最后得到了a * b * c *…条最短路径。

function path=path_all(r, start, dest)

  % r : 路由表（元胞） 
  % start : 起点index
  % dest : 终点index
  
  %初始化存储所有最短路径的矩阵path
 path=start;
 % path=r{start,dest}; 这样子写可以少算一轮，但是没有源点，不建议
  
 
 %最多经过n个点，所以迭代n次即length(r)次
 for ii=1:length(r) 
     path_new=[];
     %遍历每一列
     for iii=1:size(path,2) 
         %把每一列最后一个元素对应路由表上的点找出，
         %例如第一列最后一个元素是2，则找到r{2,10}，再遍历r{1,10}中的每个元素，把它们加到原来的列的末尾
         for new=r{path(end,iii),dest} 
             new_column=[path(:,iii);new];%新的列
             path_new=[path_new,new_column]; %把新的一列加入新的path矩阵里
         end
     end
     
     if size(path(end,:)) ==size(path_new(end,:))
     if path(end,:)==path_new(end,:) %新产生path的行和原来path的最后一行一样，则终止
     break;
     end
     end
     path=path_new;%若未终止，则迭代更新path，进入下一轮
 end
  path=path';%转置后，一行代表一条路径，更符合习惯
  
 end

使用函数

[d,r]=floyd_all(b1); %生成距离矩阵和路由矩阵
path=path_all(r,1,10); %找出1到10的所有最短路径

结果

path =

     1     2     4     7     9    10
     1     3     5     8     9    10
     1     3     6     8     9    10
     1    10    10    10    10    10

注意，这里为了保持矩阵形式对齐，有的路径末尾会有重复，例如这里的[1,10,10,10,10,10]

因为最短路径里不会出现重复点，想要调用这条路径的时候unique一下并保持顺序不变就好了

A = [1,10,10,10,10,10];
[i,j] = unique(A,'first');
A = A(sort(j));

A =

     1    10

由此得到了1-10所有最短路径，一共4条

所有最长路径

只有有向无环图才存在最长路径，如

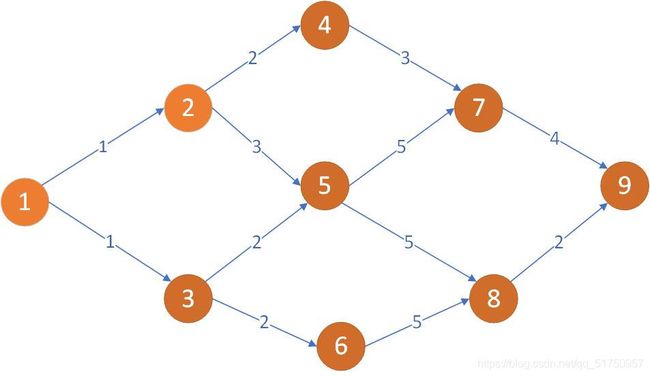
算法与最短路径完全相同，只需要改变邻接矩阵

a(a~=inf)=-a(a~=inf);%为了求最长路径，权重变为负值，但不包括inf

a =

     0    -1    -1   Inf   Inf   Inf   Inf   Inf   Inf
   Inf     0   Inf    -2    -3   Inf   Inf   Inf   Inf
   Inf   Inf     0   Inf    -2    -2   Inf   Inf   Inf
   Inf   Inf   Inf     0   Inf   Inf    -3   Inf   Inf
   Inf   Inf   Inf   Inf     0   Inf    -5    -5   Inf
   Inf   Inf   Inf   Inf   Inf     0   Inf    -5   Inf
   Inf   Inf   Inf   Inf   Inf   Inf     0   Inf    -4
   Inf   Inf   Inf   Inf   Inf   Inf   Inf     0    -2
   Inf   Inf   Inf   Inf   Inf   Inf   Inf   Inf     0

然后

[d,r]=floyd_all(a);
path=path_all(r,1,10);

path =

     1     2     5     7     9

就得到了最长路径