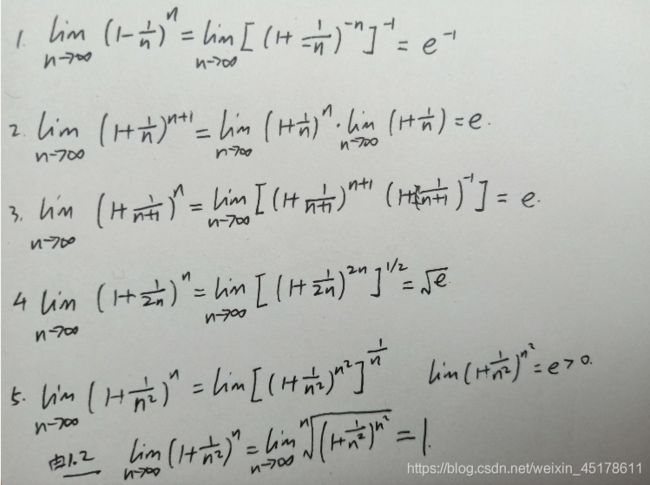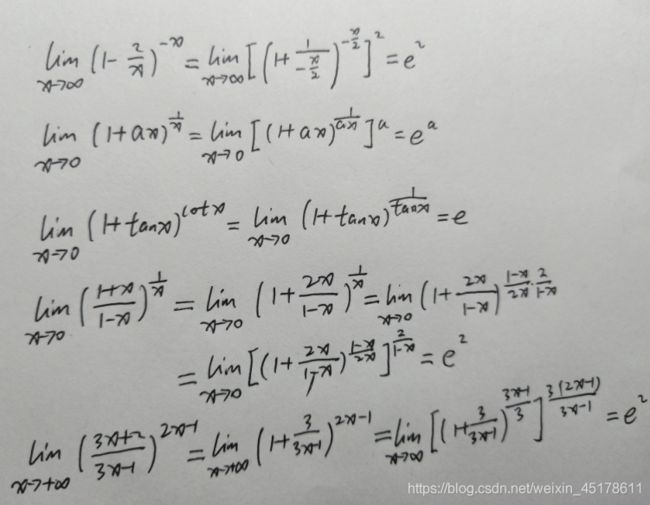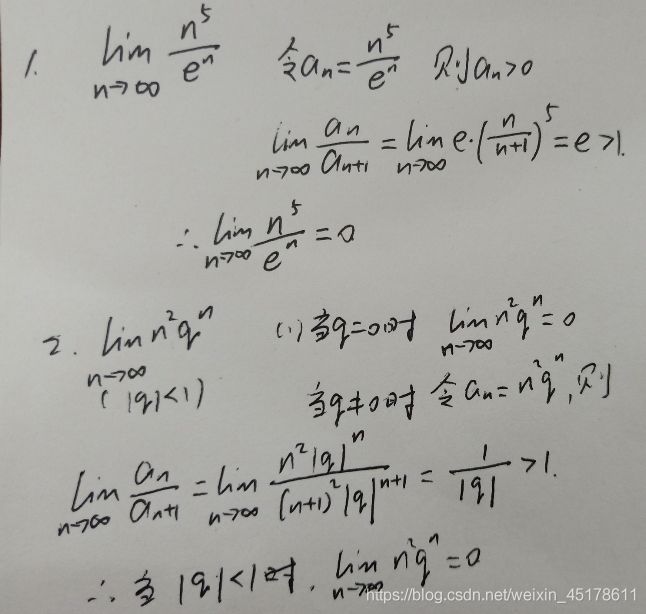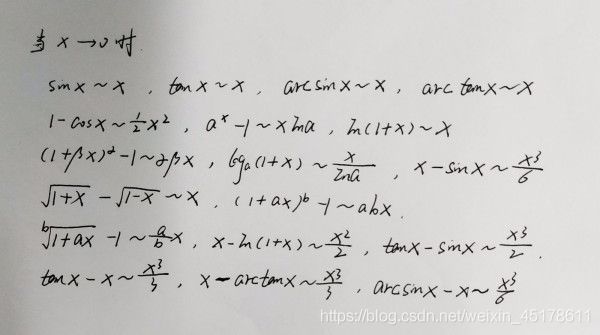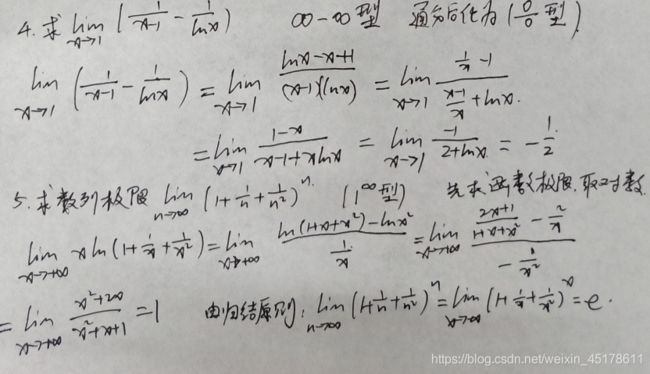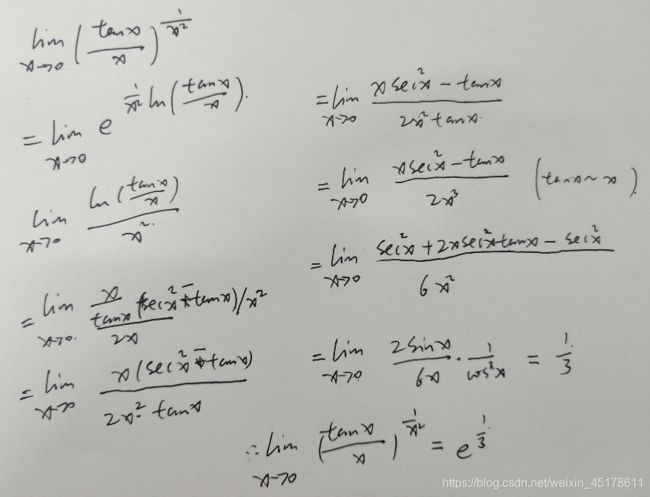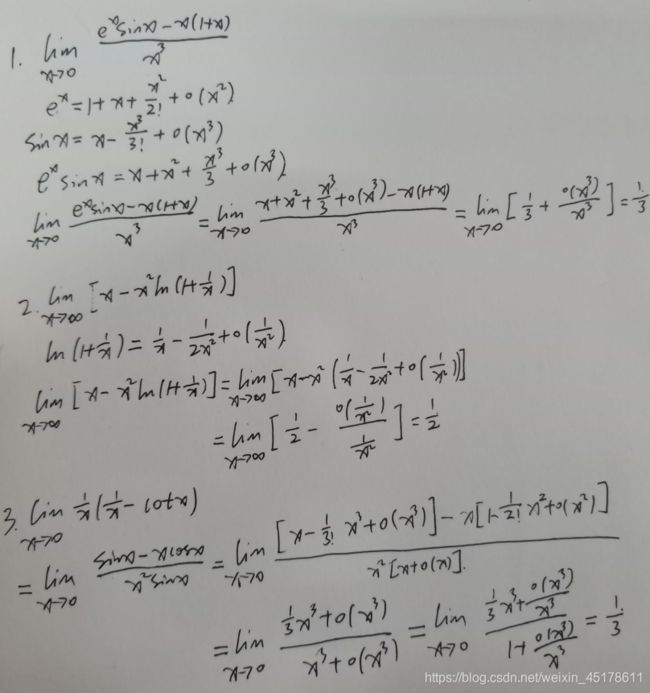考研复习 求解函数极限的方法全总结
lim x → ∞ \lim\limits_{x\rightarrow\infty} x→∞lim
lim x → x 0 \lim\limits_{x\rightarrow\ x_0} x→ x0lim
文章目录
-
- 1 几种常用的基础极限:
-
- 1.1 lim n → ∞ ( 1 + 1 n ) n = e \lim\limits_{n\rightarrow\infty}(1+\frac{1}{n})^n=e n→∞lim(1+n1)n=e (考研大纲重点:两个重要极限内容)
-
- 1.1例题
- 1.2 lim x → 0 s i n x x = 1 \lim\limits_{x\rightarrow\ 0}\frac{sinx}{x}=1 x→ 0limxsinx=1(考研大纲重点:两个重要极限内容)
-
- 1.2 例题
- 1.3 lim x → ∞ q n = 0 \lim\limits_{x\rightarrow\infty} q^n=0 x→∞limqn=0 ∣ q ∣ < 1 |q|<1 ∣q∣<1
- 1.4 lim x → ∞ a n = 1 \lim\limits_{x\rightarrow\infty}\sqrt [n]{a}=1 x→∞limna=1 a > 0 a>0 a>0
- 1.5 若 lim n → ∞ a n = a \lim\limits_{n\rightarrow\infty}a_n=a n→∞liman=a,则 lim x → ∞ a n = a , 则 lim x → ∞ 1 n ( a 1 + a 2 + . . . + a n ) = a \boldsymbol{\lim\limits_{x\rightarrow\infty}a_n=a,则\lim\limits_{x\rightarrow\infty}\frac{1}{n}(a1+a2+...+an)=a} x→∞liman=a,则x→∞limn1(a1+a2+...+an)=a
- 1.6 若 lim n → ∞ a n = a \lim\limits_{n\rightarrow\infty}a_n=a n→∞liman=a, a ≥ 0 a≥0 a≥0,则 lim x → ∞ a 1 a 2 . . . a n n = a \boldsymbol{\lim\limits_{x\rightarrow\infty}\sqrt[n]{a_1a_2...a_n}=a} x→∞limna1a2...an=a
- 1.7 若 a n > 0 a_n>0 an>0,且 lim n → ∞ a n a n + 1 = l > 1 \lim\limits_{n\rightarrow\infty}\frac{a_n}{a_{n+1}}=l>1 n→∞liman+1an=l>1,则 lim n → ∞ a n = 0 \lim\limits_{n\rightarrow\infty}a_n=0 n→∞liman=0
- 1.8 指数替换 x α = e l n x α = e α l n x \boldsymbol{x^α=e^{lnx^{α}}=e^{αlnx}} xα=elnxα=eαlnx
- 1.9 若数列{ a n a_n an}满足下列条件之一,则它是无穷大数列
- 2常用的求极限方法和性质
-
- 2.1 四则运算法则:
- 2.2 夹逼准则定义:
- 2.3 利用等价无穷小量替换
-
-
- 无穷小量概念
- 等价无穷小量:
- 等价无穷小代换的几个重要结论
- 等价无穷小量狗图(很重要):
-
- 2.4 洛必达法则
-
-
- 洛必达法则定义:
- 1. 0 0 \boldsymbol{\frac{0}{0}} 00型不定式极限
- 2. ∞ ∞ \boldsymbol{\frac{∞}{∞}} ∞∞型不定式极限
-
- 2.5 通过泰勒公式求极限
- 2.6 对于连续函数 f f f和 g g g, f f f在点 x 0 x_0 x0连续, g g g在点 u 0 u_0 u0连续, u 0 = f ( x 0 ) u_0=f(x_0) u0=f(x0),则复合函数f•g在点 x 0 x_0 x0连续
- 总结
- 附:考研大纲中有关函数极限的的要求
1 几种常用的基础极限:
1.1 lim n → ∞ ( 1 + 1 n ) n = e \lim\limits_{n\rightarrow\infty}(1+\frac{1}{n})^n=e n→∞lim(1+n1)n=e (考研大纲重点:两个重要极限内容)
引申:
形如 1 ∞ 1^∞ 1∞型的极限(底数部分极限为1,指数部分极限为无穷),大部分可化为与e有关的问题来解决
一般形式:设 f ( x ) → 1 , g ( x ) → 0 f(x)→1,g(x)→0 f(x)→1,g(x)→0,
则 lim [ f ( x ) ] g ( x ) = e l i m [ f ( x ) − 1 ] g ( x ) \lim[f(x)]^{g(x)}=e^{lim[f(x)-1]g(x)} lim[f(x)]g(x)=elim[f(x)−1]g(x)或 lim [ f ( x ) ] g ( x ) = e l i m [ g ( x ) − 1 ] f ( x ) \lim[f(x)]^{g(x)}=e^{lim[g(x)-1]f(x)} lim[f(x)]g(x)=elim[g(x)−1]f(x)
1.1例题
1.2 lim x → 0 s i n x x = 1 \lim\limits_{x\rightarrow\ 0}\frac{sinx}{x}=1 x→ 0limxsinx=1(考研大纲重点:两个重要极限内容)

引申: 一般形式: a ( x ) → 0 , lim x → x 0 s i n f ( x ) f ( x ) = 1 a(x)→0, \lim\limits_{x\rightarrow\ x_0}\frac{sinf(x)}{f(x)}=1 a(x)→0,x→ x0limf(x)sinf(x)=1
1.2 例题
1.3 lim x → ∞ q n = 0 \lim\limits_{x\rightarrow\infty} q^n=0 x→∞limqn=0 ∣ q ∣ < 1 |q|<1 ∣q∣<1
引申:
l o g a n ≪ n k ≪ c n ≪ n n \boldsymbol{log_an\ll n^k\ll c^n\ll n^n} logan≪nk≪cn≪nn ( a > 0 , k > 0 , c > 1 ) \boldsymbol{(a>0,k>0,c>1)} (a>0,k>0,c>1)
即当 n → ∞ n→∞ n→∞时, l o g a n n k , n k c n , c n n ! , n ! n n \frac{log_an}{n^k},\frac{n^k}{c^n},\frac{c^n}{n!},\frac{n!}{n^n} nklogan,cnnk,n!cn,nnn!都以0为极限,也即这些比式都是无穷小量。
换句话说,分母趋于 ∞ ∞ ∞的速度远远快于分子
记住上述不等式,可以求有关比式的极限,只要后面一项做前面一项的分母,则以0为极限
1.4 lim x → ∞ a n = 1 \lim\limits_{x\rightarrow\infty}\sqrt [n]{a}=1 x→∞limna=1 a > 0 a>0 a>0
引申:
当 n → ∞ n→∞ n→∞时, a n , n n , n k n \boldsymbol{\sqrt[n]{a},\sqrt[n]{n},\sqrt[n]{n^k}} na,nn,nnk ( a > 0 , k > 0 ) (a>0,k>0) (a>0,k>0) 均以1为极限。
然而当n次根式的内部继续增大时,结果将发生质变:
lim n → ∞ c n n = c ; \lim\limits_{n\rightarrow\infty}\sqrt[n]{c^n}=c; n→∞limncn=c; lim n → ∞ n ! n = ∞ ; \lim\limits_{n\rightarrow\infty}\sqrt[n]{n!}=∞; n→∞limnn!=∞; lim n → ∞ n n n = lim n → ∞ n = ∞ ; \lim\limits_{n\rightarrow\infty}\sqrt[n]{n^n}=\lim\limits_{n\rightarrow\infty}n=∞; n→∞limnnn=n→∞limn=∞;
1.5 若 lim n → ∞ a n = a \lim\limits_{n\rightarrow\infty}a_n=a n→∞liman=a,则 lim x → ∞ a n = a , 则 lim x → ∞ 1 n ( a 1 + a 2 + . . . + a n ) = a \boldsymbol{\lim\limits_{x\rightarrow\infty}a_n=a,则\lim\limits_{x\rightarrow\infty}\frac{1}{n}(a1+a2+...+an)=a} x→∞liman=a,则x→∞limn1(a1+a2+...+an)=a
1.6 若 lim n → ∞ a n = a \lim\limits_{n\rightarrow\infty}a_n=a n→∞liman=a, a ≥ 0 a≥0 a≥0,则 lim x → ∞ a 1 a 2 . . . a n n = a \boldsymbol{\lim\limits_{x\rightarrow\infty}\sqrt[n]{a_1a_2...a_n}=a} x→∞limna1a2...an=a
1.7 若 a n > 0 a_n>0 an>0,且 lim n → ∞ a n a n + 1 = l > 1 \lim\limits_{n\rightarrow\infty}\frac{a_n}{a_{n+1}}=l>1 n→∞liman+1an=l>1,则 lim n → ∞ a n = 0 \lim\limits_{n\rightarrow\infty}a_n=0 n→∞liman=0
1.8 指数替换 x α = e l n x α = e α l n x \boldsymbol{x^α=e^{lnx^{α}}=e^{αlnx}} xα=elnxα=eαlnx
常用在洛必达法则中,凑不定式极限
1.9 若数列{ a n a_n an}满足下列条件之一,则它是无穷大数列
(1) lim x → ∞ ∣ a n ∣ n = r > 1 \lim\limits_{x\rightarrow\infty}\sqrt[n]{|a_n|}=r>1 x→∞limn∣an∣=r>1
(2) lim x → ∞ ∣ a n + 1 a n ∣ = s > 1 \lim\limits_{x\rightarrow\infty}|\frac{a_{n+1}}{a_n}|=s>1 x→∞lim∣anan+1∣=s>1( a n ≠ 0 a_n≠0 an=0)
2常用的求极限方法和性质
2.1 四则运算法则:
设 lim x → x 0 f ( x ) \lim\limits_{x\rightarrow\ x_0}f(x) x→ x0limf(x)和 lim x → x 0 g ( x ) \lim\limits_{x\rightarrow\ x_0}g(x) x→ x0limg(x)都存在,则函数 f ± g , f ∗ g f±g,f*g f±g,f∗g当 x → x 0 x→x_0 x→x0时也存在,且
(1) lim x → x 0 [ f ( x ) ± g ( x ) ] = lim x → x 0 f ( x ) ± lim x → x 0 g ( x ) \lim\limits_{x\rightarrow\ x_0}[f(x)±g(x)]=\lim\limits_{x\rightarrow\ x_0}f(x)±\lim\limits_{x\rightarrow\ x_0}g(x) x→ x0lim[f(x)±g(x)]=x→ x0limf(x)±x→ x0limg(x)
(2) lim x → x 0 [ f ( x ) ∗ g ( x ) ] = lim x → x 0 f ( x ) ∗ lim x → x 0 g ( x ) \lim\limits_{x\rightarrow\ x_0}[f(x)*g(x)]=\lim\limits_{x\rightarrow\ x_0}f(x)*\lim\limits_{x\rightarrow\ x_0}g(x) x→ x0lim[f(x)∗g(x)]=x→ x0limf(x)∗x→ x0limg(x)
(3)若 lim x → x 0 g ( x ) ≠ 0 \lim\limits_{x\rightarrow\ x_0}g(x)≠0 x→ x0limg(x)=0,有 lim x → x 0 f ( x ) g ( x ) = lim x → x 0 f ( x ) lim x → x 0 g ( x ) \lim\limits_{x\rightarrow\ x_0} \frac{f(x)}{g(x)}=\frac{\lim\limits_{x\rightarrow\ x_0}f(x)}{\lim\limits_{x\rightarrow\\x_0}g(x)} x→ x0limg(x)f(x)=x→x0limg(x)x→ x0limf(x)
2.2 夹逼准则定义:
设 lim x → x 0 f ( x ) \lim\limits_{x\rightarrow\ x_0}f(x) x→ x0limf(x)和 lim x → x 0 g ( x ) \lim\limits_{x\rightarrow\ x_0}g(x) x→ x0limg(x)都存在,且在某邻域内有 f ( x ) ≤ g ( x ) f(x)≤g(x) f(x)≤g(x),内有
f ( x ) ≤ h ( x ) ≤ g ( x ) f(x)≤h(x)≤g(x) f(x)≤h(x)≤g(x)
则 lim x → x 0 h ( x ) = A \lim\limits_{x\rightarrow\ x_0}h(x)=A x→ x0limh(x)=A
一般类似这样的连加式子会用到夹逼准则

2.3 利用等价无穷小量替换
无穷小量概念
设 f f f在某 u 0 ( x 0 ) u^0(x_0) u0(x0)上有定义。若 lim x → x 0 f ( x ) = 0 \lim\limits_{x\rightarrow\ x_0}f(x)=0 x→ x0limf(x)=0,则称当 f f f为 x → x 0 时 的 无 穷 小 量 x→x_0时的无穷小量 x→x0时的无穷小量
等价无穷小量:
若 lim x → x 0 f ( x ) g ( x ) = 1 \lim\limits_{x\rightarrow\ x_0}\frac{f(x)}{g(x)}=1 x→ x0limg(x)f(x)=1,则称 f f f与 g g g是当 x → x 0 x→x_0 x→x0时的等价无穷小量,记作
f ( x ) ~ g ( x ) f(x) ~g(x) f(x)~g(x)
例如:由于 lim x → x 0 s i n ( x ) x = 1 \lim\limits_{x\rightarrow\ x_0}\frac{sin(x)}{x}=1 x→ x0limxsin(x)=1,故有 s i n ( x ) ~ x ( x → 0 ) sin(x)~x (x→0) sin(x)~x(x→0);
又由于 lim x → x 0 a r c t a n ( x ) x = 1 \lim\limits_{x\rightarrow\ x_0}\frac{arctan(x)}{x}=1 x→ x0limxarctan(x)=1,故有 a r c t a n ( x ) ~ x ( x → 0 ) arctan(x)~x (x→0) arctan(x)~x(x→0)
该定理作用是,求两个无穷小之比时,分子和分母都可用其等价无穷小代替,从而简化计算。
等价无穷小代换的几个重要结论
1.乘除因子项可直接用其等价无穷小代换
2.在同一个变化过程中,若一个因子是由有限个不同阶的无穷小量相加而成,则他等价于阶数最低的无穷小量
3.作为加减项的同阶的无穷小量不能随意用其等价无穷小代换。
例如:
极限 lim x → x 0 x − s i n x x 3 ≠ lim x → x 0 x − x x 3 = 0 \lim\limits_{x\rightarrow\ x_0}\frac{x-sinx}{x^3}≠\lim\limits_{x\rightarrow\ x_0}\frac{x-x}{x^3}=0 x→ x0limx3x−sinx=x→ x0limx3x−x=0
等价无穷小量狗图(很重要):
2.4 洛必达法则
洛必达法则定义:
通常把两个无穷小量之比或两个无穷大量之比的极限统称为不定式极限,分别记为 0 0 \frac{0}{0} 00型或 ∞ ∞ \frac{∞}{∞} ∞∞型的不定式极限。以导数为工具研究不定式极限,这个方法被称为洛必达法则。
1. 0 0 \boldsymbol{\frac{0}{0}} 00型不定式极限
如果函数 f f f和 g g g满足:
(i) lim x → x 0 f ( x ) = lim x → x 0 g ( x ) = 0 或 ∞ \lim\limits_{x\rightarrow\ x_0}f(x)=\lim\limits_{x\rightarrow\ x_0}g(x)=0或∞ x→ x0limf(x)=x→ x0limg(x)=0或∞
(ii)在点x_0的某空心邻域内两者都可导,且 g ′ ( x ) ≠ 0 g'(x)≠0 g′(x)=0
(iii) lim x → x 0 f ′ ( x ) g ′ ( x ) = A ( A \boldsymbol{\lim\limits_{x\rightarrow\ x_0}\frac{f'(x)}{g'(x)}=}A(A x→ x0limg′(x)f′(x)=A(A 可以为实数,也可以为无穷)
则有 lim x → x 0 f ( x ) g ( x ) \boldsymbol{\lim\limits_{x\rightarrow\ x_0}\frac{f(x)}{g(x)}} x→ x0limg(x)f(x)= lim x → x 0 f ′ ( x ) g ′ ( x ) = A \boldsymbol{\lim\limits_{x\rightarrow\ x_0}\frac{f'(x)}{g'(x)}}=A x→ x0limg′(x)f′(x)=A
对应例题:
2. ∞ ∞ \boldsymbol{\frac{∞}{∞}} ∞∞型不定式极限
如果函数 f f f和 g g g满足:
(i) 在 x 0 x_0 x0的某个右邻域内两者可导,且 g ′ ( x ) ≠ 0 g'(x)≠0 g′(x)=0;
(ii) lim x → ∞ g ( x ) = lim x → ∞ f ( x ) = + ∞ \lim\limits_{x\rightarrow\infty}g(x)=\lim\limits_{x\rightarrow\infty}f(x)=+∞ x→∞limg(x)=x→∞limf(x)=+∞;
(iii) lim x → x 0 f ′ ( x ) g ′ ( x ) = A \boldsymbol{\lim\limits_{x\rightarrow\ x_0}\frac{f'(x)}{g'(x)}}=A x→ x0limg′(x)f′(x)=A ( A A A可为实数,也可为∞)
则有 lim x → ∞ f ( x ) g ( x ) \boldsymbol{\lim\limits_{x\rightarrow\infty}\frac{f(x)}{g(x)}} x→∞limg(x)f(x)= lim x → ∞ f ′ ( x ) g ′ ( x ) = A \boldsymbol{\lim\limits_{x\rightarrow\infty}\frac{f'(x)}{g'(x)}}=A x→∞limg′(x)f′(x)=A
注意:
1.只有对 0 0 \frac{0}{0} 00型或 ∞ ∞ \frac{∞}{∞} ∞∞型的未定式可以直接使用洛必达法则
其他未定式,如 0 ∗ ∞ , 1 ∞ 0*∞,1^∞ 0∗∞,1∞等,可以通过代数运算或者取对数化为 0 0 \frac{0}{0} 00型或 ∞ ∞ \frac{∞}{∞} ∞∞型后再使用。
2.不能在数列形式下直接使用洛必达法则,因为对于离散变量,求导数是没有意义的。
3.分子分母同除以最大的项的本质是设法将表达式中的无穷大量转化为无穷小量,从而方便利用极限运算法则
对于一些满足条件的未定式,也不适合直接使用洛必达法则直接进行运算。而是通过一些其他的代数运算将其求出。例如:分子分母同时除以最高项、极限的四则运算法则、用常见的基础极限转化等。
2.5 通过泰勒公式求极限
一些常见的泰勒公式(带有佩亚诺型余项的麦克劳林公式)
e x = 1 + x + x 2 2 ! + . . . + x n n ! + 0 ( x n ) e^x=1+x+\frac{x^2}{2!}+...+\frac{x^n}{n!}+0(x^n) ex=1+x+2!x2+...+n!xn+0(xn)
s i n x = x − + x 3 3 ! + x 5 5 ! + . . . + ( − 1 ) m − 1 x 2 m − 1 ( 2 m − 1 ) ! + 0 ( x 2 m ) sinx=x-+\frac{x^3}{3!}+\frac{x^5}{5!}+...+(-1)^{m-1}\frac{x^{2m-1}}{(2m-1)!}+0(x^{2m}) sinx=x−+3!x3+5!x5+...+(−1)m−1(2m−1)!x2m−1+0(x2m)
c o s x = 1 − x + x 2 2 ! + x 4 4 ! . . . + ( − 1 ) m x 2 m ( 2 m − 1 ) ! + 0 ( x 2 m + 1 ) cosx=1-x+\frac{x^2}{2!}+\frac{x^4}{4!}...+(-1)^{m}\frac{x^{2m}}{(2m-1)!}+0(x^{2m+1}) cosx=1−x+2!x2+4!x4...+(−1)m(2m−1)!x2m+0(x2m+1)
l n ( 1 + x ) = x − x 2 2 + x 3 3 . . . + ( − 1 ) n − 1 x n n ! + 0 ( x n ) ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}...+(-1)^{n-1}\frac{x^n}{n!}+0(x^n) ln(1+x)=x−2x2+3x3...+(−1)n−1n!xn+0(xn)
( 1 + x ) α = 1 + α x + α ( α − 1 ) 2 ! x 2 + . . . + α ( α − 1 ) . . . ( α − n + 1 ) n ! x n + 0 ( x n ) (1+x)^α=1+αx+\frac{α(α-1)}{2!}x^2+...+\frac{α(α-1)...(α-n+1)}{n!}x^n+0(x^n) (1+x)α=1+αx+2!α(α−1)x2+...+n!α(α−1)...(α−n+1)xn+0(xn)
1 1 − x = 1 + x + x 2 + . . . + x n + 0 ( x n ) \frac{1}{1-x}=1+x+x^2+...+x^n+0(x^n) 1−x1=1+x+x2+...+xn+0(xn)
当用常规方法“洛”或者无穷小代换比较复杂时,可以直接使用泰勒公式代换
一般情况下只留三到四项。对于 0 0 \frac{0}{0} 00型的未定式极限,

例题
2.6 对于连续函数 f f f和 g g g, f f f在点 x 0 x_0 x0连续, g g g在点 u 0 u_0 u0连续, u 0 = f ( x 0 ) u_0=f(x_0) u0=f(x0),则复合函数f•g在点 x 0 x_0 x0连续
存在
lim x → x 0 f ( g ( x ) ) = g ( lim x → x 0 f ( x ) ) = g ( f ( x 0 ) ) \lim\limits_{x\rightarrow\ x_0}f(g(x))=g(\lim\limits_{x\rightarrow\ x_0}f(x))=g(f(x_0)) x→ x0limf(g(x))=g(x→ x0limf(x))=g(f(x0))
不仅对 x → x 0 x→x_0 x→x0这种类型的极限成立,而且对 x → ± ∞ x→±∞ x→±∞, x → x 0 ± x→x_0^{±} x→x0±也存在。
总结
1.求极限的方法有很多,常用的有四则运算法则、夹逼准则、无穷小量代换、洛必达法则、泰勒公式等等,再配合一些基础的极限变换。一般考题中,会同时考到两到三个方法(考点)。因此当面对一道题只用到一种方法时需要检查解法是否正确!
2.未定式极限的基本形式是 ∞ ∞ \frac{∞}{∞} ∞∞和 0 0 \frac{0}{0} 00,其他未定式都可转化为这两种形式。求未定式的主要方法是洛必达法则,但一般情况下不可以直接求,需要通过无穷小量代换、四则运算法则、提非零因子式等等方法。
3.无穷小量代换狗图、泰勒公式变换和基础极限变换要熟记。
4.上述题大部分来自数分书和考研复习全书,后期还要做更多的题